深度学习——线性回归和softmax回归
智能2112杨阳
一、目的
- 线性回归的从零开始实现及简洁实现
- softax回归的从零开始实现及简洁实现
二、环境
vscode(d2l,torch,pandas)
希冀平台
三、内容
1、线性回归
a、生成数据集
def synthetic_data(w, b, num_examples): #@save
"""生成y=Xw+b+噪声"""
b、读取数据集
data_iter函数,该函数接收批量大小、特征矩阵和标签向量作为输入,生成大小为batch_size的小批量。每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels):
c、初始化模型参数
torch.normal(means, std, out=None)均值,标准差,可选的输出张量
d、定义模型
线性回归模型:y=wx+b
def linreg(X, w, b): #@save
"""线性回归模型"""
e、定义损失函数
# y_hat是预测值, y是真实值
def squared_loss(y_hat, y): #@save
"""均方损失"""
f、定义优化算法
sgd(params, lr, batch_size): #@save
"""小批量随机梯度下降"""
g、训练
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
# 'X'和'y'的小批量损失
# 因为'l'形状是('batch_size',1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l = loss(net(X, w, b), y) # X和y的小批量损失
# 求和之后算梯度,这里backward()会对w和b进行求导
l.sum().backward()
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
# net(features, w, b):预测值
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
2、softmax回归
a、载入数据集
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
b、初始化模型参数
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
c、定义softmax操作
# 定义softmax函数
def softmax(X):
X_exp = torch.exp(X) # 对每个元素做指数运算
partition = X_exp.sum(1, keepdim=True) # 对每行进行求和
return X_exp / partition # 这里应用了广播机制
d、定义模型
def net(X):
return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
e、定义损失函数
# 定义交叉熵损失函数
def cross_entropy(y_hat, y):
return - torch.log(y_hat[range(len(y_hat)), y])
cross_entropy(y_hat, y)
f、分类精度
def accuracy(y_hat, y): #@save
"""计算预测正确的数量"""
def evaluate_accuracy(net, data_iter): #@save
"""计算在指定数据集上模型的精度"""
class Accumulator: #@save
"""在n个变量上累加"""存储正确预测的数量和预测的总数量
g、训练
def train_epoch_ch3(net, train_iter, loss, updater): #@save
"""训练模型一个迭代周期"""
将模型设置为训练模式#
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save
"""训练模型"""
h、预测
def predict_ch3(net, test_iter, n=6): #@save
"""预测标签"""
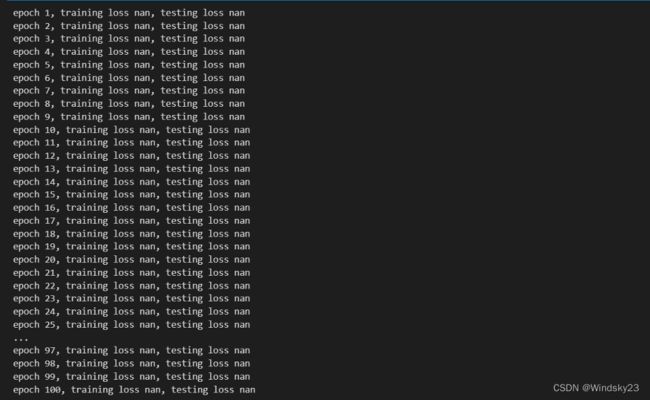
3、给定一个temper.CSV文件,前三列为样本数据特征,最后一列为标签,模仿”线性回归实现“训练模型并查看损失。其中会出现什么问题并给出解决方案。
问题及解决方案:
1、数据预处理问题:线性回归通常需要对数据进行预处理,包括特征缩放、处理缺失值、处理异常值等。如果数据没有经过适当的预处理,可能会导致模型训练过程中出现问题,如梯度爆炸或梯度消失。
解决方案:确保对数据进行适当的预处理,包括对特征进行标准化或归一化,处理缺失值和异常值等。
2、过拟合问题:线性回归模型可能面临过拟合的问题,即在训练集上表现良好但在测试集上表现较差。过拟合可能是因为模型过于复杂,导致过多的参数需要拟合训练数据,从而无法很好地泛化到新数据。
解决方案:可以通过引入正则化技术,如L1正则化(Lasso)或L2正则化(Ridge),来减少模型的复杂度。另外,可以使用交叉验证来选择最佳的超参数,以避免过拟合。
3、收敛问题:模型训练可能遇到收敛问题,即模型无法达到最优解或训练过程非常缓慢。
解决方案:可以尝试调整学习率(learning rate)来控制参数更新的步长,选择合适的优化算法,如随机梯度下降(SGD)或Adam优化器,以加快模型收敛速度。
4、特征选择问题:线性回归模型的性能可能受到特征选择的影响。如果选择了不相关或冗余的特征,可能会导致模型性能下降。
解决方案:可以使用特征选择方法,如相关系数、L1正则化等,来选择对目标变量有较强相关性的特征,以提高模型性能。
5、高维度问题:当特征维度很高时,线性回归模型可能面临求解困难或计算资源消耗过大的问题。
解决方案:可以考虑使用降维技术,如主成分分析(PCA)或特征选择方法,来减少特征的维度,从而简化模型求解过程。
代码:
输出结果:
四、总结
问题及解决方法:d2l包安装失败,下载轮子后重新pip安装成功
这次博客让我对线性回归和softmax回归有了一定的了解和认识,训练softmax回归循环模型与训练线性回归模型非常相似:先读取数据,再定义模型和损失函数,然后使用优化算法训练模型。虽然学习了很多,但是仍然无法熟练运用线性回归和softmax回归的相关知识,还需要加强对python的学习及相关知识的学习,总的来说收获满满。