层次聚类和密度聚类思想及实现
层次聚类
层次聚类的概念:
层次聚类是一种很直观的算法。顾名思义就是要一层一层地进行聚类。
层次法(Hierarchicalmethods)先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后,再 计算类与类之间的距离,将距离最近的类合并为一个大类。不停的合并,直到合成了一个类。其中类与类 的距离的计算方法有:最短距离法,最长距离法,中间距离法,类平均法等。比如最短距离法,将类与类 的距离定义为类与类之间样本的最短距离。
层次聚类算法根据层次分解的顺序分为:自下底向上和自上向下,即凝聚的层次聚类算法和分裂的层次聚 类算法(agglomerative和divisive),也可以理解为自下而上法(bottom-up)和自上而下法(top- down)
凝聚层次聚类的流程:
凝聚型层次聚类的策略是先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有对 象都在一个簇中,或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类,它们只是在簇间 相似度的定义上有所不同。
这里给出采用最小距离的凝聚层次聚类算法流程:
(1) 将每个对象看作一类,计算两两之间的最小距离;
(2) 将距离最小的两个类合并成一个新类;
(3) 重新计算新类与所有类之间的距离;
(4) 重复(2)、(3),直到所有类最后合并成一类。
特点:
• 凝聚的层次聚类并没有类似K均值的全局目标函数,没有局部极小问题或是很难选择初始点的问题。
• 合并的操作往往是最终的,一旦合并两个簇之后就不会撤销。
• 当然其计算存储的代价是昂贵的。
层次聚类的优缺点:
优点:
1,距离和规则的相似度容易定义,限制少;
2,不需要预先制定聚类数;
3,可以发现类的层次关系;
4,可以聚类成其它形状
缺点:
1,计算复杂度太高;
2,奇异值也能产生很大影响;
3,算法很可能聚类成链状
代码实现:
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z) #层级聚类结果以树状图表示出来并保存
print(Z)
plt.show()
代码解读:
1.linkage(X, 'ward')
函数功能:进行层次聚类/凝聚聚类
linkage(y, method=’single’, metric=’euclidean’) 共包含3个参数:
(1) y是距离矩阵,可以是1维压缩向量(距离向量),也可以是2维观测向量(坐标矩阵)。
若y是1维压缩向量,则y必须是n个初始观测值的组合,n是坐标矩阵中成对的观测值。
(2)method是指计算类间距离的方法。
method = ‘single’
d(u,v) = min(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最近邻点算法。
method = 'complete’
d(u,v) = max(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最近邻点算法。
method = 'average’
|u|,|v|是聚类u和v中元素的的个数,这被称为UPGMA算法(非加权组平均)法。
method = 'weighted’
d(u,v) = (dist(s,v) + dist(t,v))/2
u是由s和t形成的,而v是森林中剩余的聚类簇,这被称为WPGMA(加权分组平均)法。
method = ‘ward’ (沃德方差最小化算法)
新的输入d(u,v)通过下式计算得出:
u是s和t组成的新的聚类,v是森林中未使用的聚类。T = |v|+|s|+|t|,|*|是聚类簇中观测值的个数
参考来源聚类算法(五)——层次聚类 linkage (含代码)
2.fcluster(Z,4,'distance')
fcluster(Z, t, criterion=’inconsistent’, depth=2, R=None, monocrit=None)
(1)第一个参数Z是linkage得到的矩阵,记录了层次聚类的层次信息;
(2)t是一个聚类的阈值。
Z代表了利用“关联函数”关联好的数据。
比如上面的调用实例就是使用欧式距离来生成距离矩阵,并对矩阵的距离取平均
这里可以使用不同的距离公式
t这个参数是用来区分不同聚类的阈值,在不同的criterion条件下所设置的参数是不同的。
比如当criterion为’inconsistent’时,t值应该在0-1之间波动,t越接近1代表两个数据之间的相关性越大,t越趋于0表明两个数据的相关性越小。这种相关性可以用来比较两个向量之间的相关性,可用于高维空间的聚类
depth 代表了进行不一致性(‘inconsistent’)计算的时候的最大深度,对于其他的参数是没有意义的,默认为2
criterion这个参数代表了判定条件,这里详细解释下各个参数的含义:
(1)当criterion为’inconsistent’时,t值应该在0-1之间波动,t越接近1代表两个数据之间的相关性越大,t越趋于0表明两个数据的相关性越小。这种相关性可以用来比较两个向量之间的相关性,可用于高维空间的聚类
(2)当criterion为’distance’时,t值代表了绝对的差值,如果小于这个差值,两个数据将会被合并,当大于这个差值,两个数据将会被分开。
(3)当criterion为’maxclust’时,t代表了最大的聚类的个数,设置4则最大聚类数量为4类,当聚类满足4类的时候,迭代停止
(4)当criterion为’monocrit’时,t的选择不是固定的,而是根据一个函数monocrit[j]来确定。
参考来源python的scipy层次聚类参数详解
结果展示:

结果解读:
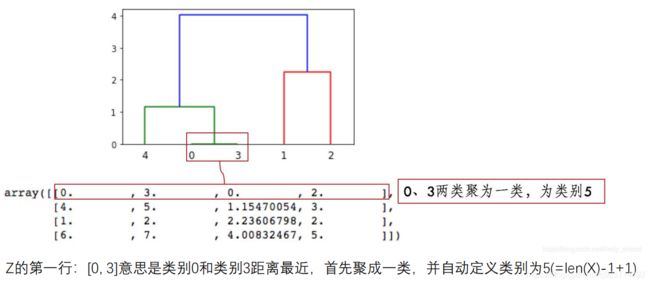

第三行、第四行以此类推, 因为类别5有两个样本,加上类别4形成类别6,有3个样本;
类别7是类别1、2聚类形成,有两个样本;
类别6、7聚成一类后,类别8有5个样本,这样X全部样本参与聚类,聚类完成。
Z第四列中有样本的个数,当最下面一行中的样本数达到样本总数时,聚类就完成了。
想分两类时,就从上往下数有两根竖线时进行切割,那么所对应的竖线下面所连接的为一类
想分三类时,就从上往下数有三根竖线时进行切割,那么所对应的竖线下面所连接的为一类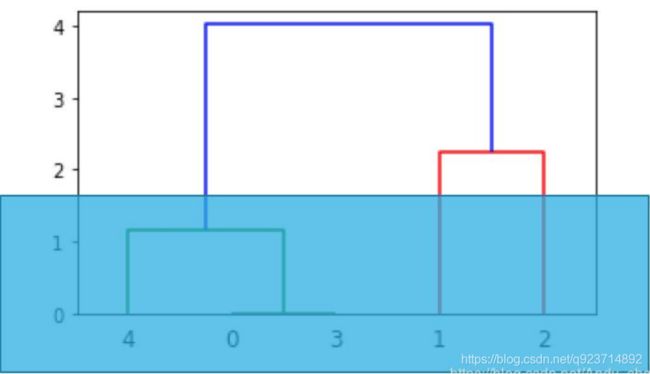
每一种聚类方法都有其特定的数据结构,对于服从高斯分布的数据用K-Means来进行聚类效果 会比较好。 而对于类别之间存在层结构的数据,用层次聚类会比较好。
密度聚类
密度聚类算法思想:
需要两个参数:ε (eps) 和形成高密度区域所需要的最少点数 (minPts)
• 它由一个任意未被访问的点开始,然后探索这个点的 ε-邻域,如果 ε-邻域里有足够的点,则建立一 个新的聚类,否则这个点被标签为杂音。
• 注意,这个点之后可能被发现在其它点的 ε-邻域里,而该 ε-邻域可能有足够的点,届时这个点会被 加入该聚类中。
密度聚类的优缺点:
优点:
1.对噪声不敏感;
2.能发现任意形状的聚类。
缺点:
1.但是聚类的结果与参数有很大的关系;
2.用固定参数识别聚类,但当聚类的稀疏程度不同时,相同的判定标准可能会破坏聚类的自然结构, 即较稀的聚类会被划分为多个类或密度较大且离得较近的类会被合并成一个聚类。
代码实现:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.cluster import DBSCAN
iris = datasets.load_iris()
X = iris.data[:, :4] # #表示我们只取特征空间中的4个维度
print(X.shape)
# 绘制数据分布图
'''
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
'''
dbscan = DBSCAN(eps=0.4, min_samples=9)
#eps是两个点的距离不大于eps时为一类,min_samples是指每个类最少min_samples个点
dbscan.fit(X)
#对x进行聚类
label_pred = dbscan.labels_
# 绘制结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
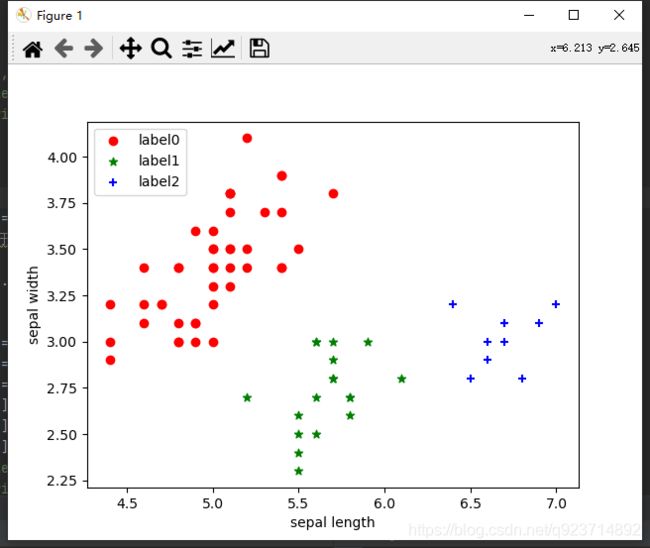
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()