java开发面试:LinkedList底层数据结构分析、和ArrayList的区别是什么、HashMap(底层数据结构哈希表精讲,put方法、扩容机制源码分析、在java版本中的不同、死循环问题)
LinkedList
底层数据结构——双向链表
单向链表
查询/添加/删除时间复杂度
查询:头节点:O(1),一般情况:O(n)
增删:头节点:O(1),一般情况:O(n)
双向链表
查询/添加/删除时间复杂度
查询:头尾节点:O(1),一般情况:O(n),给定节点找前驱节点:O(1)
增删:头尾节点:O(1),一般情况:O(n),给定节点找前驱节点:O(1)
和ArrayList的区别是什么
从四个方面来谈。
- 底层数据结构
- 效率
- 空间
- 线程是否安全
-
底层数据结构上,
ArrayList 是动态数组的数据结构实现
LinkedList 是双向链表的数据结构实现 -
效率上,除了 LinkedList不支持下标查询,ArrayList支持下标查询。其他都差不多。
-
空间上,ArrayList底层是数组,内存连续,节省内存。
LinkedList 是双向链表需要存储数据,和两个指针,更占用内存。 -
线程安全问题,ArrayList和LinkedList都不是线程安全的。
如果需要保证线程安全,有两种方案:- 在方法内使用,局部变量则是线程安全的
- 使用线程安全的ArrayList和LinkedList
Collections.synchronizedList(new ArrayList<>()); Collections.synchronizedList(new LinkedList<>());
HashMap
底层数据结构——哈希表(散列表)
二叉树
在二叉树中,比较常见的二叉树有:
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 红黑树
二叉搜索树/BST树
二叉搜索树(Binary Search Tree,BST)又名二叉查找树,有序二叉树或者排序二叉树,是二叉树中比较常用的一种类型。
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
一般情况下,其插入,查找,删除的时间复杂度都为O(logn)。
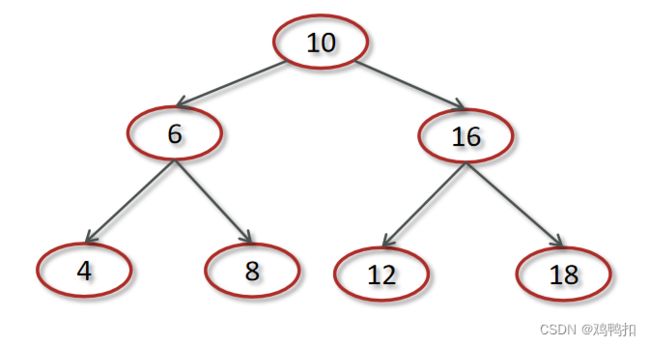
但是,二叉查找树会存在退化成链表的情况,左右子树极度不平衡,此时查找的时间复杂度肯定是O(n)。为此,衍生出了红黑树。
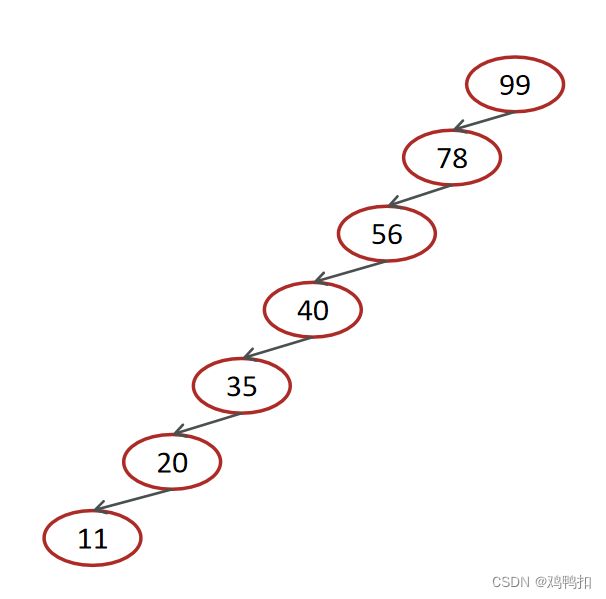
红黑树
红黑树:也是一种自平衡的二叉搜索树(BST),之前叫做平衡二叉B树。
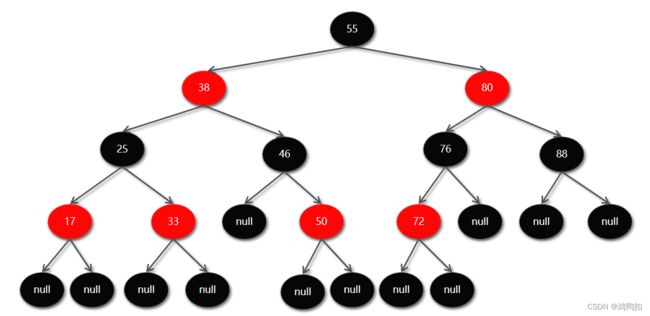
红黑树有五大性质。
性质1:节点要么是红色,要么是黑色
性质2:根节点是黑色
性质3:叶子节点都是黑色的空节点
性质4:红黑树中红色节点的子节点都是黑色
性质5:从任一节点到叶子节点的所有路径都包含相同数目的黑色节点
在添加或删除节点的时候,如果不符合这些性质会发生旋转,以达到所有的性质,由此保障了树的平衡。所以其插入,查找,删除的时间复杂度都为O(logn)。
哈希表(散列表)
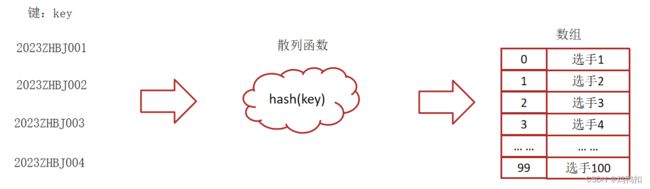
散列表(Hash Table)又名哈希表/Hash表,是根据键(Key)直接访问在内存存储位置值(Value)的数据结构,它是由数组演化而来的,利用了数组支持按照下标进行随机访问数据的特性。
将键(key)映射为数组下标的函数叫做散列函数。
一个理想状态下的散列函数满足以下三点:
散列函数计算得到的散列值必须是大于等于0的正整数,因为hashValue需要作为数组的下标。
如果key1==key2,那么经过hash后得到的哈希值也必相同即:hash(key1) == hash(key2)
如果key1 != key2,那么经过hash后得到的哈希值也必不相同即:hash(key1) != hash(key2)
但实际上,想找一个散列函数能够做到对于不同的key计算得到的散列值都不同几乎是不可能的,即便像著名的MD5,SHA等哈希算法也无法避免这一情况,这就是散列冲突(或者哈希冲突,哈希碰撞,就是指多个key映射到同一个数组下标位置)。
拉链法
在散列表中,数组的每个下标位置我们可以称之为桶(bucket)或者槽(slot),每个桶(槽)会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
即数组那接个链表过来。
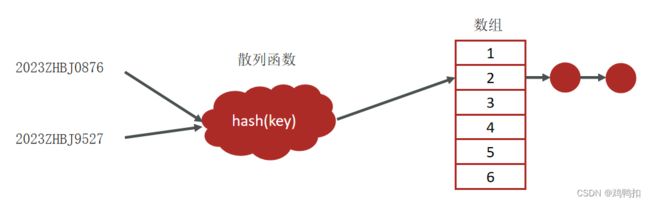
插入:O(1)
查找或删除时:一般基于单链表的拉链法为O(1),单链表退化为链表时为O(n)
所以将拉链法中的链表改造为其他高效的动态数据结构,比如红黑树,保证了查询的时间复杂度是 O(logn),同时,一定程度上防止了DDos攻击。
一定程度上防止了DDos攻击的原因:
攻击者可以通过故意构造冲突,使得散列表中某个位置的链表过长,从而耗尽系统的资源。
而使用红黑树可以避免链表过长的问题,因为红黑树的平衡性保证了树的高度较低,从而减少了搜索的时间复杂度。这可以一定程度上抵御攻击者对散列表的DDoS攻击。
HashMap在java 1.7和1.8中的不同
JDK1.8之前采用的是拉链法。若遇到哈希冲突,则将冲突的值加到链表中即可。
JDK1.8在解决哈希冲突时有了较大的变化,当链表长度大于阈值(默认为8) 时并且数组长度达到64时,将链表转化为红黑树,以减少搜索时间。扩容 resize( ) 时,红黑树拆分成的树的结点数小于等于临界值6个,则退化成链表.
hashmap在1.7情况下的多线程死循环问题
建议直接看如下视频:
https://www.bilibili.com/video/BV1K44y1d7JJ
图解比较清晰,比B站大多数只会文字讲面试回答的视频要好。
其讲的内容也是本篇文章下面一些内容,建议看完,可以互补。
源码分析
成员变量
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //初始容量,默认为1<<4,实际就是16
static final float DEFAULT_LOAD_FACTOR = 0.75f;//加载因子,默认为0.74
transient HashMap.Node<K,V>[] table;//实际存储数据的键值对数组
//因为是懒惰加载,所以在创建HashMap对象时并没有初始化数组
transient int size;//实际存储数据的个数
当实际存储数据的个数(size)==最大容量threshod时,进行扩容。
最大容量threshod=数组长度(table.length)*加载因子(DEFAULT_LOAD_FACTOR)
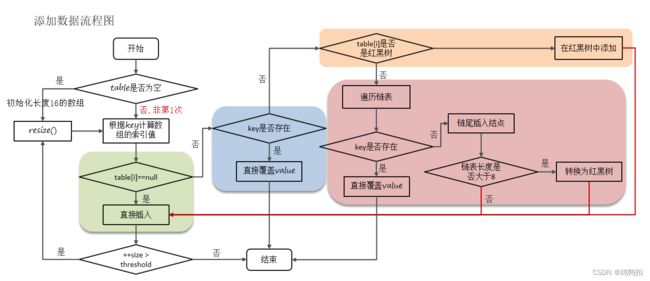
put方法源码分析
- 判断键值对数组table是否为空或为null,否则执行resize()进行扩容(初始化)
- 根据键值key计算hash值得到数组索引
- 判断table[i]==null,条件成立,直接新建节点添加。
- 如果table[i]==null ,不成立,说明该位置有链表或者红黑树。
4.1 判断table[i]的首个元素是否和key一样,如果相同直接覆盖value。
4.2 判断table[i] 是否为treeNode,即table[i] 是否是红黑树,如果是红黑树,则直接在树中插入键值对。
4.3 遍历table[i],链表的尾部插入数据,然后判断链表长度是否大于8,大于8的话把链表转换为红黑树,在红黑树中执行插入操 作,遍历过程中若发现key已经存在直接覆盖value。 - 插入成功后,判断实际存在的键值对数量size是否超多了最大容量threshold(数组长度*0.75),如果超过,进行扩容。
resize()方法源码分析/扩容机制
注意以下流程都是jdk1.8为例。且将旧数组的容量DEFAULT_INITIAL_CAPACITY 简记为oldcap,新数组的容量DEFAULT_INITIAL_CAPACITY 简记为newcap。
- 在添加元素或初始化的时候需要调用resize方法进行扩容,第一次添加数据初始化数组长度为16,以后每次扩容都是达到了扩容阈值threshold(数组长度(table.length) * 0.75)
- 每次扩容的时候,都是之前容量的2倍,即newcap=2*oldcap
- 扩容之后,会新创建一个数组,需要把老数组中的数据挪动到新的数组中
3.1 没有红黑树或链表的节点,使用 e.hash & (newcap - 1) 计算该元素在新数组的索引位置。
3.2 如果是红黑树,走红黑树的添加。
3.3 如果是链表,则需要遍历链表,可能需要拆分链表,判断(e.hash & newcap)是否为0。- 如果为0,说明不需要拆分链表,该元素的位置停留在原始位置
- 如果不为0,说明需要拆分链表,该元素移动到原始位置+oldcap这个位置上
实际上就是数学公式。
如果e.hash&newcap为0,那么其e.hash&(newcap-1)和e.hash&(oldcap-1)一定一样。
如果e.hash&newcap不为0,那么其e.hash&(newcap-1)和e.hash&(oldcap-1)不一样。
在这里就是用e.hash&newcap是否为0代替了判断,以及判断中可能需要的计算(e.hash&(newcap-1)),从而提升了效率。
可以看下这篇博客,举了一个例子:http://t.csdnimg.cn/evyJe
寻址算法
源码如下:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
HashMap计算索引,即得到hash,需要经过以下三个步骤:
- 调用对象的 hashCode()(java中任意对象都有这个方法)
- 再进行调用 hash() 方法进行二次哈希, hashcode值右移16位再异或运算,让哈希分布更为均匀
- 最后 (capacity – 1) & hash 得到索引
如果只有第一步hashCode()得到hash,那么不能保障元素的分布是比较均匀的。
于是我们想到了得到的hashCode再对数组长度取模运算(hashCode%length),但是如果hashCode比较大,取模计算的开销也会很大。那么因为数学上(hashCode%length)和(hashCode&(length-1))是等效的,那么我们就用按位与运算代替了取模运算,这也就是第三步的来源。
即使如此,因为一般情况下length都是int类型,也就是说一般都会小于2^16次方,那么也只会和hashCode的低16位打交道,这样导致按位与运算后出来的hash值依旧散列度不高,即分布不够均匀。因此,我们首先将hashCode右移16位,意味着把hashCode的高位移动到了低位。
然后再用hashCode与右移之后的值进行异或运算,就相当于把高位和低位的特征进行组合,从而增强了hashCode本身的散列度。
至于为什么要用异或运算,用其他位运算也可以结合高位和低位的特征啊。
这是因为以下是位运算的结果。可以看到异或的分布最为均匀,不会1占多数或者0占多数,也就是说高位或低位的影响力差不多。
| 位运算 | 1和1 | 1和0 | 0和0 | 0和1 |
|---|---|---|---|---|
| 与 | 1 | 0 | 0 | 0 |
| 或 | 1 | 1 | 0 | 1 |
| 异或 | 0 | 1 | 0 | 1 |
这也就是第二步的来源。
为何HashMap的数组长度一定是2的次幂?
首先,计算索引时效率更高:如果是 2 的 n 次幂可以使用位与运算代替取模
第二,扩容时重新计算索引效率更高: hash & oldCap == 0 的元素留在原来位置 ,否则新位置 = 旧位置 + oldCap
(所以如果我们初始化HashMap时传入的初始容量不是2的次幂,HashMap会自动调整成2的次幂。)