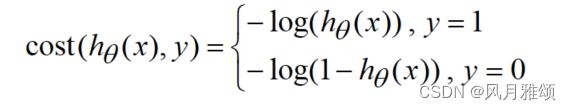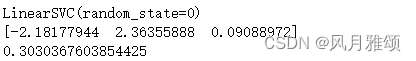机器学习——损失函数
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。
1、简介
损失函数(loss function)又称为误差函数(error function),是衡量模型好坏的标准,用于估量模型的预测值与真实值的不一致程度,是一个非负实值函数。损失函数的一般表示为L(y,f(x)),用以衡量真实值y与预测值f(x)不一致的程度,一般越小越好。
损失函数对模型进行评估,并且为模型参数的优化提供了方向。损失函数的选取依赖于参数的数量、异常值、机器学习算法、梯度下降的效率、导数求取的难易和预测的置信度等。
损失函数与代价函数(cost function)相似,可以互换使用。区别在于,损失函数用于单个训练样本。而代价函数是整个训练数据集的所有样本误差的平均损失。
损失函数有回归损失(regression loss)和分类损失(classification loss)两类。
2、回归损失
2.1 MAE
平均绝对误差(Mean Absolute Error, MAE)又称L1损失,是指预测值与真实值之间平均误差的大小,反映了预测值误差的实际情况,用于评估预测结果和真实数据集的接近程度。其值越小,说明拟合效果越好。
平均绝对误差的表达形式为
![]()
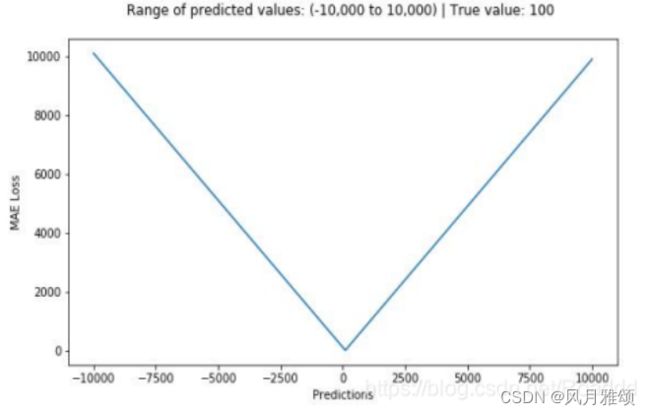
MAE 函数示例,其中,真实目标值为100,预测值为-10 000~10000。预测值(Predictions)为100时,MAE 损失(MAE Loss)达到其最小值。损失范围为[0,![]() ]。
]。
Sklearn提供了mean_absolute_error函数用于求平均绝对误差,格式如下:
sklearn.metrics.mean_absolute_error(y_true, y_pred)【参数说明】
- y_true:真实值。
- y_pred:预测值。
2.2 MSE
均方误差(Mean Squared Error,MSE)又称L2损失,是最常用的回归损失评估指标,反映了观测值与真值偏差的平方之和与观测次数的比值,是预测值与真实值之差的平方之和的平均值。其值越小,说明拟合效果越好。
均方误差的表达形式为
![]()
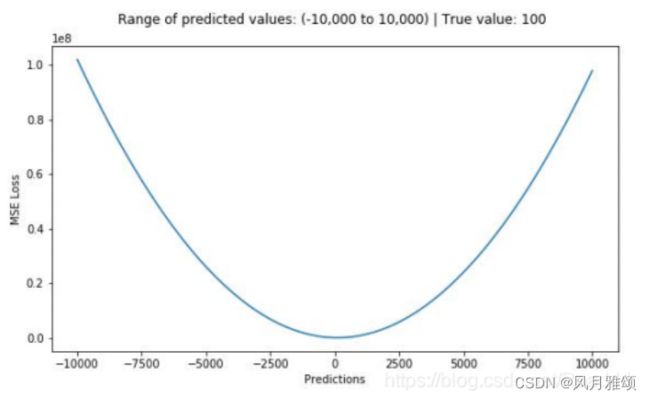
MSE 函数示例,其中,真实目标值为100,预测值为一10 000~10 000。预测值(Predictions)为100时,MSE 损失(MSE Loss)达到其最小值。损失范围为[0,![]() ]。
]。
Sklearn提供了mean_squared_error函数用于求均方误差,格式如下:
sklearn.metrics.mean_squared_error(y_true, y_pred)【参数说明】
- y_true:真实值。
- y_pred:预测值。
2.3 RMSE
RMSE 是根均方误差(Root Mean Square Error),其取值范围为[0,+![]() )。其表达为:
)。其表达为:
![]()
取均方误差的平方根可以使得量纲一致,这对于描述和表示有意义。
2.4 R2分数
分类问题用F1_score进行评价。在回归问题中,相应的评价标准是决定系数(coefficient of determination),又称为![]() 分数,简称
分数,简称![]() 。使用同一算法模型解决不同的问题,由于数据集的量纲不同,MSE,RMSE 等指标不能体现模型的优劣。而
。使用同一算法模型解决不同的问题,由于数据集的量纲不同,MSE,RMSE 等指标不能体现模型的优劣。而![]() 分数的取值范围是[0,1],越接近1,表明模型对数据拟合较好;越接近0,表明模型拟合较差。
分数的取值范围是[0,1],越接近1,表明模型对数据拟合较好;越接近0,表明模型拟合较差。
Sklearn提供了r2_score函数用于表示决定系统,格式如下:
sklearn.metrics.r2_score(y_true, y_pred)回归损失示例:
import numpy as np
from sklearn import metrics
from sklearn.metrics import r2_score
y_true = np.array([1.0,5.0,4.0,3.0,2.0,5.0,-3.0])
y_pred = np.array([1.0,4.5,3.5,5.0,8.0,4.5,1.0])
#mae
print("MAE:", metrics.mean_absolute_error(y_true, y_pred))
#MSE
print('MSE:', metrics.mean_squared_error(y_true, y_pred))
#RMSE
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
#R Squared
print('R Square:', r2_score(y_true, y_pred))【运行结果】
2.5 Huber损失
均方损失(MSE)对于异常点进行较大惩罚,不够健壮。平均绝对损失(MAE)对于较多异常点表现较好,但在y-f(x)=0处不连续可导,不容易优化。
L1损失函数与L2损失函数对比如表所示。
| L1损失函数 | L2损失函数 |
| 健壮 | 不够健壮 |
| 不稳定解 | 稳定解 |
| 可能多个解 | 总是一个解 |
Huber 损失是对MSE 和MAE 缺点的改进。
当|y-f(x)|小于指定的![]() 值时,Huber 损失变为平方损失;
值时,Huber 损失变为平方损失;
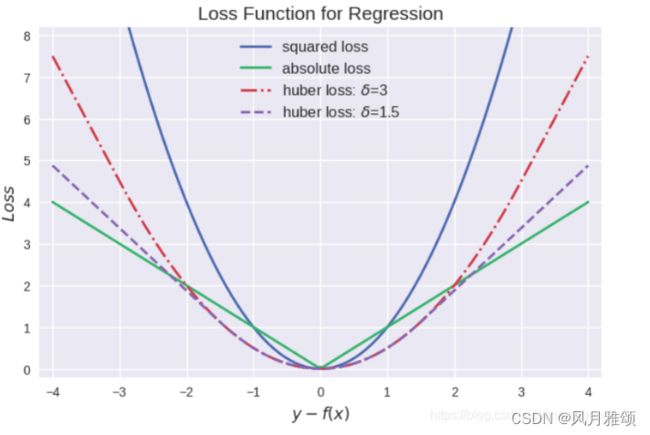
当大于![]() 值时,Huber 损失类似于绝对值损失。回归损失函数对比如图所示。
值时,Huber 损失类似于绝对值损失。回归损失函数对比如图所示。
sklearn.linear_model提供了HuberRegressor函数用于Huber损失,格式如下:
huber = HuberRegressor()示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import HuberRegressor
y_train = np.array([368, 340, 376, 954, 331, 856])
x_train = np.array([1.7, 1.5, 1.3, 5, 1.3, 2.2])
plt.scatter(x_train, y_train, label = 'Train Samples')
x_train = x_train.reshape(-1,1)#reshape(-1,1)转换成1列:
#L2损失函数
lr = LinearRegression()
lr.fit(x_train, y_train)
a = range(1,6)
b = [lr.intercept_ + lr.coef_[0] * i for i in a]#.intercept_截距;.coef_权重
plt.plot(a, b, 'r', label = "Train Samples")
#Huber 损失函数
huber = HuberRegressor()
huber.fit(x_train, y_train)
a = range(1,6)
b = [huber.intercept_ + huber.coef_[0] * i for i in a]
plt.plot(a, b, 'b', label = 'Train Samples')
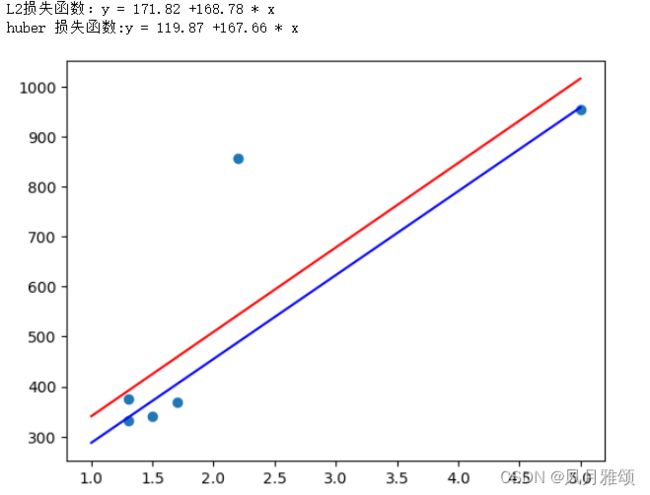
print('L2损失函数:y = {:.2f} +{:.2f} * x'.format(lr.intercept_, lr.coef_[0]))
print("huber 损失函数:y = {:.2f} +{:.2f} * x".format(huber.intercept_, huber.coef_[0]))【运行结果】
3、分类损失
3.1常见损失函数
- 平方损失函数。
- 绝对误差损失函数。
- 0-1损失函数。
- 对数损失函数。
- 铰链损失函数。
3.2 平方损失函数
平方损失(squared loss)函数计算实际值和预测值之差的平方,又称为L2损失函数,一般用在线性回归中,可以理解为最小二乘法。其表达形式为
![]()
相应的成本函数是这些平方误差的平均值(MSE)。
3.3 绝对误差损失函数
绝对误差损失(absolute error loss)函数计算预测值和实际值之间的距离,用在线性回归中。绝对误差损失函数也称为L1损失函数。绝对误差损失函数的表达形式为
![]()
相应的成本函数是这些绝对误差的平均值(MAE)。
3.4 0-1损失函数
0-1损失(zero-one loss)函数当预测标签和真实标签一致时返回0,否则返回1。0-1损失函数的表达形式为
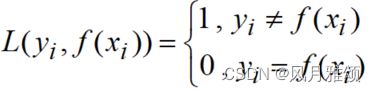
Sklearn 提供了zero_one_loss函数,格式如下:
sklearn.metrics.zero_one_loss(y_true, y_pred, normalize)【参数说明】
- y_true:真实值。
- y_pred:预测值。
- normalize:取值为True,返回平均损失;取值为 False,返回损失之和。
示例:
from sklearn.metrics import zero_one_loss
import numpy as np
#二分类问题
y_pred = [1,2,3,4]
y_true = [2,2,3,4]
print(zero_one_loss(y_true, y_pred))
print(zero_one_loss(y_true, y_pred, normalize = False))
#多分类问题
print(zero_one_loss(np.array([[0,1],[1,1]]), np.ones((2,2))))
print(zero_one_loss(np.array([[0,1],[1,1]]), np.ones((2,2)), normalize = False))3.5 对数损失函数
当预测值和实际值的误差符合高斯分布,使用对数损失(logarithmic loss)函数,其主要应用在逻辑回归中。对数损失函数的数学表达式是如下分段函数:
当y=0时,表示真实值不属于这个类别。
Sklearn提供了log_loss函数,语法如下:
sklearn.metrics.log_loss(y_true,y_pred)示例:
from sklearn.metrics import log_loss
y_true = [0,0,1,1]
y_pred = [[0.9, 0.1], [0.8, 0.2], [0.3, 0.7], [0.01, 0.99]]
print(log_loss(y_true, y_pred))3.6 铰链损失函数
铰链损失函数(hinge Loss)函数用于评价支持向量机。Sklearn 提供了hinge_loss函数,格式如下:
sklearn.metrics.hinge_loss(y_true,y_pred)
示例:
from sklearn import svm
from sklearn.metrics import hinge_loss
x = [[0],[1]]
y = [-1, 1]
est = svm.LinearSVC(random_state = 0)
print(est.fit(x, y))
pred_decision = est.decision_function([[-2], [3], [0.5]])
print(pred_decision)
print(hinge_loss([-1, 1, 1], pred_decision))【运行结果】