机器学习优化器（公式+代码）

随机梯度下降（Stochastic Gradient Descent，SGD）

随机梯度下降（Stochastic Gradient Descent，SGD）是一种常用的优化算法，用于训练机器学习模型。它的主要思想是在每次迭代中，随机选择一个样本来估计梯度，并更新模型参数。相比于传统的梯度下降算法，SGD具有更快的收敛速度和更低的计算成本。但是，SGD也存在一些问题，如随机性和收敛性方面的问题。

import numpy as np

# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]

# 设置超参数
eta = 0.1  # 学习率
n_iterations = 1000  # 迭代次数
m = 100  # 样本数量

# 随机初始化模型参数
theta = np.random.randn(2, 1)

# 使用SGD训练模型
for iteration in range(n_iterations):
    random_index = np.random.randint(m)
    xi = X_b[random_index:random_index+1]
    yi = y[random_index:random_index+1]
    gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
    theta = theta - eta * gradients

# 输出模型参数
print(theta)

Adagrad

Adagrad是一种自适应学习率算法，它可以根据每个参数的历史梯度值来调整学习率，从而加快深度神经网络的训练速度。具体来说，Adagrad算法会为每个参数维护一个历史梯度平方和的累加量，并将其用于调整该参数的学习率。

具体步骤如下：

1. 初始化参数的历史梯度平方和为0。

2. 对于每个迭代步骤，计算参数的梯度。

3. 将参数的历史梯度平方和加上该参数的梯度平方。

4. 计算该参数的学习率为初始学习率除以历史梯度平方和的平方根。

5. 使用学习率来更新参数。

import torch
import torch.nn as nn
import torch.optim as optim

# 定义神经网络
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(10, 5)
        self.fc2 = nn.Linear(5, 1)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# 定义训练数据和标签
data = torch.randn(100, 10)
labels = torch.randn(100, 1)

# 初始化神经网络和Adagrad优化器
net = Net()
optimizer = optim.Adagrad(net.parameters(), lr=0.01)

# 训练神经网络
for i in range(100):
    optimizer.zero_grad()
    output = net(data)
    loss = nn.functional.mse_loss(output, labels)
    loss.backward()
    optimizer.step()

# 输出训练后的参数
print(net.state_dict())

Adadelta

Adadelta是一种优化方法，是Adagrad的改进。Adadelta的分母中采用距离当前时间点比较近的累计项，这可以避免在训练后期，学习率过小。Adadelta的主要思想是根据过去的梯度来调整学习率，以便更好地适应当前的梯度。Adadelta使用了两个累加变量，一个是平方梯度的指数加权平均值，另一个是平方步长的指数加权平均值。

squared_grad = E[g^2]_t
squared_dx = E[delta_x^2]_t-1
g = compute_gradient(params)
delta_x = - RMS[squared_dx] / RMS[squared_grad] * g
params += delta_x

Adam

Adam是一种自适应学习率的优化算法，它结合了Adagrad和RMSprop的优点。Adam使用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。相对于传统的随机梯度下降法，Adam算法在训练深度神经网络时收敛更快，且通常可以获得更好的泛化性能。

import tensorflow as tf

# 定义一个简单的神经网络
model = tf.keras.Sequential([
    tf.keras.layers.Dense(64, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dense(10, activation='softmax')
])

# 编译模型，使用Adam优化器
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 训练模型
model.fit(train_images, train_labels, epochs=5)

AdaMax

AdaMax是一种深度学习优化算法，它是Adam算法的一种变体。与Adam算法不同，AdaMax使用L-infinity范数来计算梯度的指数移动平均值，而不是像Adam算法一样使用L2范数。这使得AdaMax对于具有较大梯度范数的参数更加稳定。

公式如下：

mt = beta1 * mt-1 + (1 - beta1) * gt
vt = max(beta2 * vt-1, abs(gt))
theta = theta - alpha / (1 - beta1) * mt / (vt + epsilon)

示例：

import tensorflow as tf

# 定义损失函数和优化器
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
optimizer = tf.keras.optimizers.Adamax(learning_rate=0.001)

# 训练模型
for epoch in range(num_epochs):
    for x_batch, y_batch in train_dataset:
        with tf.GradientTape() as tape:
            logits = model(x_batch, training=True)
            loss_value = loss_fn(y_batch, logits)
        grads = tape.gradient(loss_value, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

Nadam

Nadam是一种深度学习优化算法，是Adam算法的一种变形形式。与Adam算法相比，Nadam算法在处理梯度时引入了Nesterov动量，可以更好地处理局部最小值问题。以下是Nadam算法的原理和实现步骤：

1. Nadam算法原理： Nadam算法是Adam算法的一种变形形式，它在Adam算法的基础上引入了Nesterov动量。Nadam算法的主要思想是在Adam算法的基础上，使用Nesterov动量来更好地处理局部最小值问题。具体来说，Nadam算法在计算梯度时，使用了Nesterov动量来更好地估计下一步的梯度，并且在更新参数时，使用了Adam算法的更新公式。

2. Nadam算法实现步骤： Nadam算法的实现步骤与Adam算法类似，主要包括以下几个步骤： （1）初始化参数：初始化模型参数和动量参数。 （2）计算梯度：使用反向传播算法计算梯度，并使用Nesterov动量来估计下一步的梯度。 （3）更新参数：使用Adam算法的更新公式来更新参数。 （4）重复步骤2和3，直到达到收敛条件。

   import numpy as np
   
   def nadam(grad_func, x_init, lr=0.001, beta1=0.9, beta2=0.999, eps=1e-8, max_iter=1000):
       # 初始化参数
       x = x_init
       m = np.zeros_like(x)
       v = np.zeros_like(x)
       t = 0
       # 计算梯度
       grad = grad_func(x)
       while t < max_iter:
           t += 1
           # 计算动量参数
           m = beta1 * m + (1 - beta1) * grad
           v = beta2 * v + (1 - beta2) * np.square(grad)
           # 计算修正后的动量参数
           m_hat = m / (1 - np.power(beta1, t))
           v_hat = v / (1 - np.power(beta2, t))
           # 计算Nesterov动量
           nesterov_m = beta1 * m_hat + (1 - beta1) * grad
           # 更新参数
           x -= lr * nesterov_m / (np.sqrt(v_hat) + eps)
           # 计算梯度
           grad = grad_func(x)
       return x

Momentum

Momentum是一种优化算法，用于加速深度学习模型的训练。它基于梯度下降算法，通过积累之前梯度的指数加权平均数来更新权重，从而加速模型的收敛速度。Momentum算法的主要思想是在梯度下降的基础上，加入了动量的概念，使得在参数更新时，不仅仅考虑当前的梯度，还考虑之前的梯度对当前参数的影响。这样可以使得参数更新的方向更加稳定，避免在参数更新时出现震荡的情况。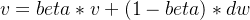 

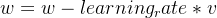
RMSprop

RMSprop是一种优化算法，用于训练神经网络。它是一种自适应学习率方法，可以根据梯度的大小自动调整每个参数的学习率。RMSprop采用了指数加权移动平均(exponentially weighted moving average)来计算梯度平方的移动平均值，并将其除以学习率。这有助于解决AdaGrad算法中学习率过快下降的问题。RMSProp比AdaGrad只多了一个超参数，其作用类似于动量(momentum)，其值通常置为0.9。

import numpy as np

def rmsprop(parameters, gradients, cache, learning_rate, decay_rate):
    """
    :param parameters: 神经网络的参数
    :param gradients: 梯度
    :param cache: RMSprop缓存
    :param learning_rate: 学习率
    :param decay_rate: 衰减率
    :return: 更新后的参数和缓存
    """
    eps = 1e-8
    for i in range(len(parameters)):
        cache[i] = decay_rate * cache[i] + (1 - decay_rate) * gradients[i] ** 2
        parameters[i] -= learning_rate * gradients[i] / (np.sqrt(cache[i]) + eps)
    return parameters, cache

总结一下，优化器是深度学习中的一种算法，用于调整模型的参数以最小化损失函数。

在训练神经网络时，我们需要通过反向传播算法计算损失函数对于每个参数的梯度，然后使用优化器来更新这些参数。优化器的作用是通过调整学习率、动量等参数，使得模型能够更快地收敛并且达到更好的效果。常用的优化器有SGD，Adam，Adagrad，RMSprop，Momentum。