HIT-2022spr-形式语言自动机期末复习

HIT-2022spr-形式语言自动机期末复习

HIT-王春宇老师-网课网址

DFA/NFA/RegularExpression

正则表达式是一种表示正则语言的方法，ε若为正则表达式，则表示{ε}这个语言，而不是空语言。

注意+是并运算，而不是两个串的连接。

正则语言的运算↑

1. FA->RegExp

2. RegExp->FA

3. 封闭性（）

正则语言在所有运算下都是封闭的

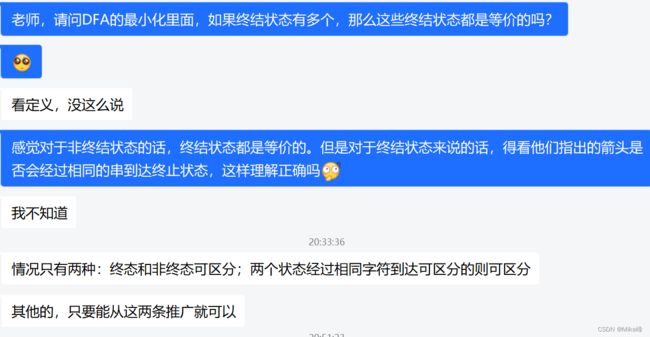
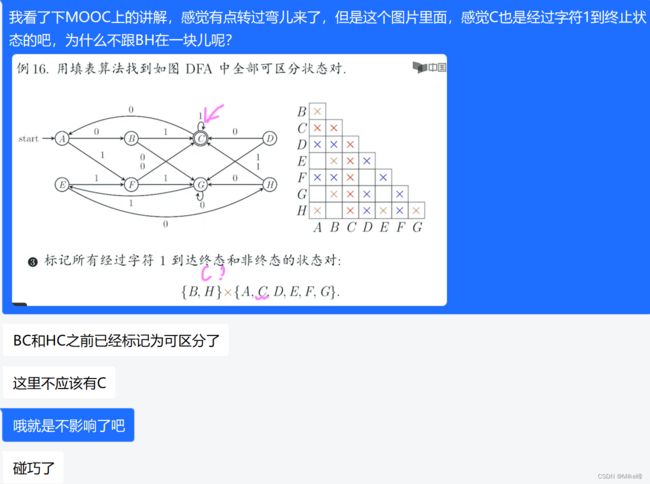
4. DFA最小化

关于终态是否等价的解释以及对于算法的规定的强调：

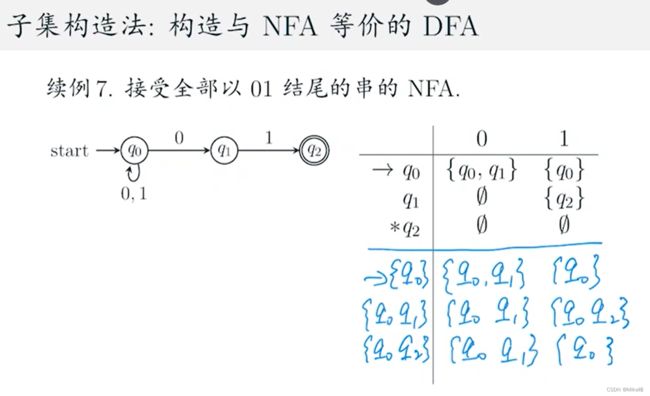
5. NFA转化成DFA(子集构造法)

6. ε-NFA转化为DFA

注意左侧的都是计算的ε-闭包，也就是说下面左面一列手写的{q0}实际上是q0的一个ε-闭包，手写的第一行第二个{q0}也是q0的闭包，也就是要求两次闭包。

PDA

1. PDA的定义

PDA通过 ε-NFA 加上 栈 的方式定义
ε-NFA：就是具有空转移以及不确定的能力

不确定性的例子：

（注意转移函数的因变量是状态的集合）

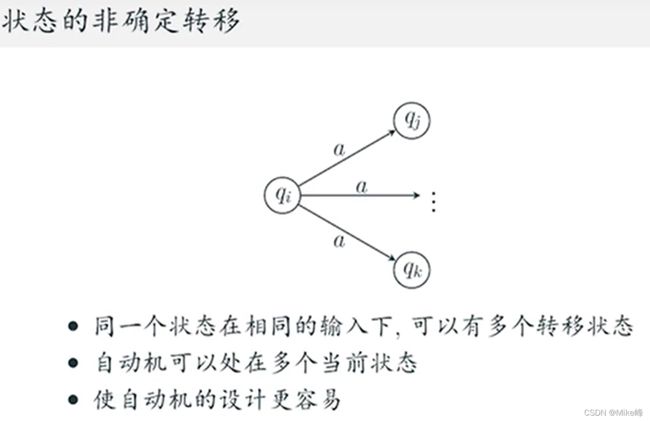
例如这个读了0可以跳转到不同位置：

2. DPDA的定义

将PDA的ε转移能力保留，但是去掉它的非确定性能力(对于最后的ε,只能说有路就要走)，就变成了DPDA。

这种语言无法接受$w{w}^r$类型的串串儿，因为DPDA不具有不确定性，无法判定到哪是$w$和$w^r$的交界处，但是DPDA可以接受$wc{w}^r$的语言。

3. PDA的栈

这里面的栈，push可以是一个字符串，但是pop的必须是一个字符。
每次输入带的读头读入一个字符，并向后移入一个单元格。此时会进行状态的修改，对于符号栈的读写头先pop栈顶的**一个字符**，然后push一个**字符串**.

4. 关于PDA题目的思路

一般来说就是硬干，但是加上空转移考虑就简单些，空转移的妙用可以使画的PDA看起来更清晰易懂。

两种PDA: (需要注意: 两种PDA都需要读完串儿才能结束)

注意：这两种PDA是等价的！！！，而DPDA才会出现终态比空栈多接受前缀语言的情况！！！

1. 接受空栈
   这种PDA无法接受前缀语言（可是终态可以）
   接受空栈的PDA最终栈是需要 $Z_0|ϵ$ 进行清空栈的操作的，在读完串儿之前是不能将$Z_0$进行弹出的。
2. 终止状态
   终止状态的PDA不需要考虑栈的情况，最终即使是栈没有清空（不管栈怎么样）只要到了终止状态就会结束。

CFG

1. 记牢CFG的形式定义

$G=(V,T,P,S)$
其中：
$V$为变元的有穷集/非终结符
$T$为终结符集合
$P$为产生式的有穷集合
$S$为初始符号
其中$S\in V$

2. PDA转CFG

PDA:
$P_{PDA}=(Q,\Sigma ,\Gamma ,\delta ,q_0,Z_0,\varphi )$

构造的CFG:
$G=(V,T,P,S)$
$\delta (q,a,X)的集合包含:(p,Y_1{Y}_2...Y_n)$

也就是说在q的状态下读取字符a，弹出栈顶符号X，就会压入栈中一个字符串$Y_1{Y}_2...Y_n$

思想：在栈中一个个弹出栈符号等价于一个个读入输入串。
也就是：为了从栈中完全弹出某一个栈符号，需要输入带上消耗掉一部分的输入串。
消耗掉的这部分输入串与栈中弹出的同栈中弹出的栈符号是一种对应关系。
如果将栈符号看成一个变元的话，相当于栈符号的变元可以派生出来被消耗掉的输入带上的输入串。
利用这样的方式来表示PDA弹空栈的一个文法。
文法的变元就对应了PDA的栈符号。but,弹出相同的栈符号，如果前后状态不同的话，读入的符号也有可能不同，所以在栈符号的前后加上相应的状态加以区分。

注意：带方括号的是变元，也就是非终止符，要是终止符还得像图片里面的a那个单独的明确的符号。

其实个人理解，能这样表示很大一个原因在于，PDA弹栈每次只能弹一个字符

这样，我们将p弹出栈顶X到达q状态的一个步骤表示写成一个变元$[pXq]$
举个小例子：

列式的依据就是要把栈中的元素全部弹空到达某一个状态（因此在列式的时候，并不知道箭头左侧q弹完z，也就是全部弹空栈中元素之后会到哪（以(1)中的第一个式子为例））

3. CFG转PDA

很容易理解：
例如：
解法:

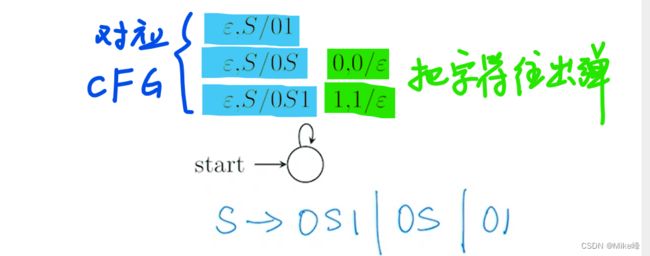
注意是空栈的接收方式，注意S会被弹出，因为只要S生成终结符串（如01），那么S就没了

4. CFL封闭性

上下文无关语言的封闭性：

CFL在并、连接、闭包、正闭包、代换(一个符号/串对应一个语言)、同态(一个符号/串对应另一个语言中的符号)、逆同态、反转
注意CFL对交、补、差运算均不封闭。但是正则语言与CFL的交为CFL。

5. 关于CFG题目的思路

(1)一种挺好的思想，我暂且称作杂交法。如何构造$a^i{b}^j$的语言，使得$j<i<2j$?
方法：
构造一个D=aaHb|ε这个串，是前面是后面的二倍，再将这个串串外面套上一堆abS=aSb|D。这样就是1倍2倍之间的了。

6. CFG化简

化简原因：
1, 有些变元是本身就无法生成的，若是放在箭头左边整一个新的产生式就多余了
2, 有的产生式不产生全部是终结符的式子
3, 有的产生ε也是多余的
化简的方法：

关于ε-产生式的化简
方法：找出箭头左边到底哪个是可空的，例如A为空，则然后在各个式子里面将空带入|将A保留（俩操作都需要），A若是本身能生成ε，那么把ε也删掉，注意那种隐蔽的A生成B，结果B可空的情况，这个时候A、B都是可空的。
目的在于要将原来的语言仅仅去掉一个空字符串，其余保留。
例如2019第七题：

Let L be the language generated by the grammar G below
S->AB|BBB
A->Bb|ε
B->aB|A
(1).消除空产生式
(2).消除单元产生式
(3).转换到CNF

这个题里面注意AB都是可空，所以在第一问的时候要把AB都进行ε的带入|保留A(或B) 的操作

消除单元产生式
先找到单元对如[A,B]，然后进行B（在箭头左侧，要复制的是B箭头右侧的东西）到A（箭头右侧）的复制，然后将箭头右侧的A删掉(***而不是替换，因为有的时候没有要交换的地方)
确定单元对的方法：

消除无用符号


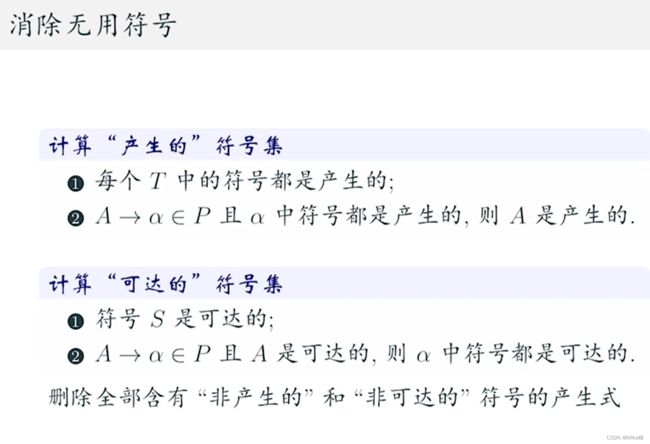
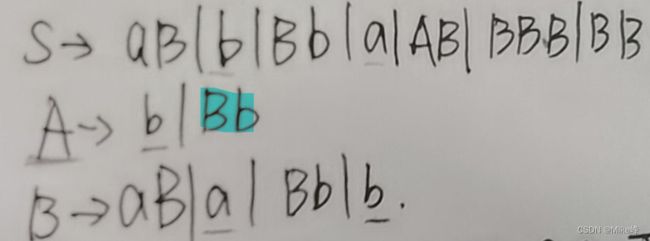
注意这个Bb也是产生的，不一定需要有一个式子Bb专门生成一个东东就判定，只需要根据B和b都是产生的就可以得到Bb是产生的。
注意：ε也是终结符

7. 化成乔姆斯基范式CNF格里巴赫范式GNF

GNF：相对于有线性文法的区别就是右线性文法里面，箭头右侧的$\alpha$只能是零个或一个变元，而GNF里面的$\alpha$可以是零个或者多个变元的串。

基本的带入方法：

代入代入代入！！！
后面那两个特殊情况完成之后也需要代入！！！

特殊情况：

间接左递归要化成直接左递归之后才能代入！！！
例题：

8. 语法分析树

对于一个CFL可以有多个CFG，每个CFG在表示某个串的时候可能会有多种语法分析树（也就是多种派生方式）

Turing Machine

图灵机的定义：

我们要求的图灵机是不允许空转移的。
而且由于我们的基本图灵机的每个移动都是确定的，因此我们研究的图灵机是 ”确定的图灵机“
可是这种图灵机并不是Q x Σ的每个子集都是有对应的Q x Σ x L/R的，以下面的状态转移表为例：

需要注意的细节与区分对比

(1)

要求画NFA，不能画ε-NFA。如果跟你说要画有穷状态自动机，也就是FA，那么啥都可以（就是NFA、ε-NFA、DFA都可以）。

(2)几种语言/自动机的对比

1.语言

上下文无关语言CFL对应的自动机是PDA也就是下推自动机(但是空栈PDA要少接受一种前缀语言)，对应的文法是上下文无关文法CFG
确定的上下文无关语言DCFL对应的自动机是确定的下推自动机DPDA（注意是终态方式接受的）
DCFL无法识别L(wwr),因此DCFL真包含于CFL
正则语言RegularLanguage对应的是DFA，而DFA、NFA、ε-NFA、正则表达式在接受语言的意义上来看是等价的
图灵机接受的语言为递归可枚举语言Recursively enumerable language

Regular Language感觉没给形式定义，但是给了正则表达式的语法：

CFG的定义，是一个四元组：

2.自动机

DFA是一个5元组：

NFA是一个五元组，与DFA的转移函数有所不同:

ε-NFA转移函数多了一个读入ε的功能

PDA为七元组，多了一个栈符号集以及栈底符号：

DPDA为七元组，但是与PDA并不等价

图灵机是7元组：
总结起来，可以发现，FA都是基础性的5元组，而其他的自动机则是在FA的五元组基础上加上各自特色的两个元素组成七元组

(3)区分两个PumpingLemma

正则语言的：

xyz, xy限制大小, y不空, 泵y
例子：

CFG的：

uvwxy, 限制vwx, vx不空, 泵vx
也就是谁不空泵谁，但是大小小于N的限制这两引理还是有区别的

(4)区分文法/表达式与语言

正则文法/正则表达式 -> 正则语言
上下文无关文法 -> 上下文无关语言

Problem Review

Problem 4

1.Construct a Turing machine that accepts L = { w ∈ {a, b}* | w has an equal number of a’s and b’s}.
答案：

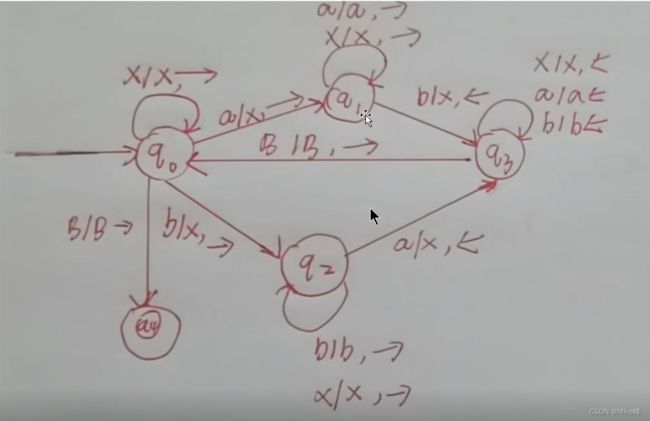
就是开头分情况要敢写，构造图灵机的过程更像一个从头到尾过一遍的过程，当然还要考虑最初始的那个状态直接跳到终止状态的的情况。

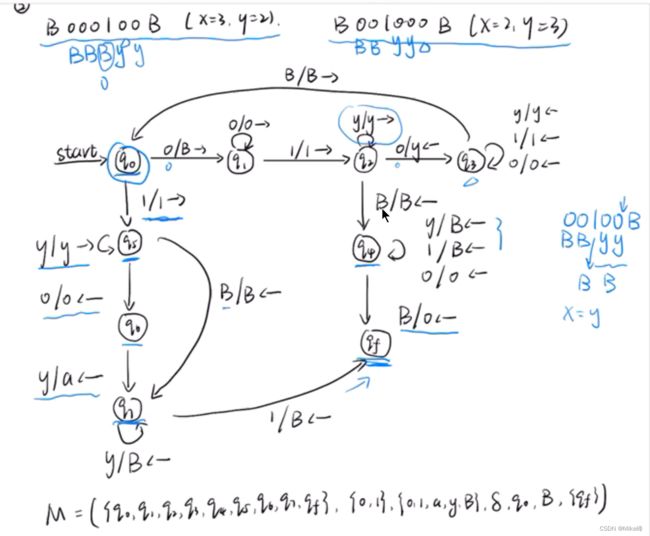
2.Let x and y are positive numbers. Please design a Turing Machine (diagram) to compute x – y of x and y). You should explain the notation of x and y. Hint : you may get the notation as simple as you can.
注意这道题需要考虑结果为负数的情况！

3.Use the CFL pumping lemma to show that the following language is not context free
$a^i{b}^j{c}^k|i<j<k$
注：CFL的泵引理如图

设$a^N{b}^{N+1}{c}^{N+2}$即可证明
4.If L1 and L2 be two CFL’s. Is it necessarily true that L1 − L2 is also a CFL? Prove your answer.
这里面问题类型是CFL的闭包
这道题实际上答案是并不构成闭包
首先应该知道一些知识：ww并不是CFL而非ww的语言却是（全集是{0,1}*）
所以这么一看差运算并不能使CFL满足运算封闭
另外$0^N{1}^{N^2}$也不是CFL

另外一个感受是要看看孙大烈的problem和PPT（当然wcy网课最好也看）

5.Show that the regular languages are closed under the following operations: min(L) = { w | w is in L, but no proper prefix of w is in L }.
这里面要求证明的是正则语言的封闭性
也就是说，我们只要构造出来对应的FA就可以了
这个方法就是将终态之后的箭头都指向一个死状态（而且是非终止状态）

6.Prove. For every context-free language L, the language $L‘=\{0^{|w|}|w\in L\}$ is also context-free.
这里利用了CFL同态的封闭性：

需要学习的知识点：

1. 右线性文法和DFA的关系：DFA可以用右线性文法进行表示，方法就是把DFA中的状态当作变元，每次造访完一个状态就产生一个读完的字符，这个字符右侧的变元是新到达的状态
2. DPDA
3. 文法的歧义性
4. GNF：见前面