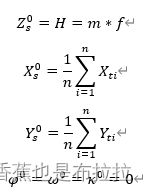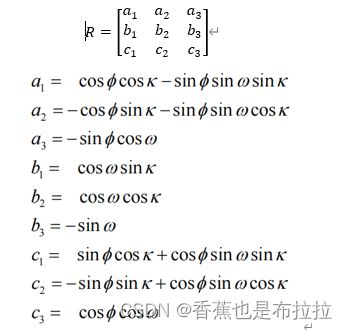利用C++实现单片空间后方交汇
总流程
代码实现具体流程图如下:
数据处理与class对象创建
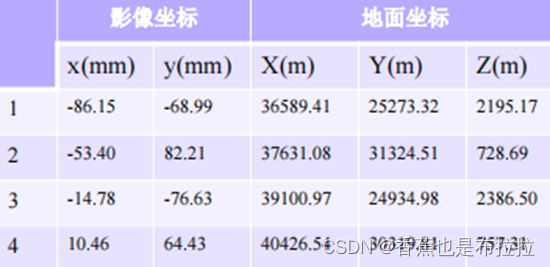
提供数据如下:
四个控制点与像点如图所示,焦距f = 153.24 mm,比例尺m = 50000。在编程过程中,我们采用三个对象(class)进行处理,分别为 imagePoint,terrainPoint, Resection。前两个类代表像点与地面点,Resection类代表后方交汇过程,包括变量与函数,具体定义如下:
class imagePoint // 像点,提供数据为毫米,注意单位换算
{
public:
double x;
double y;
imagePoint(double _x, double _y) :x(_x), y(_y) {}
};
class terrainPoint // 地面点,提供数据为米
{
public:
double x;
double y;
double z;
terrainPoint(double _x, double _y, double _z) :x(_x), y(_y), z(_z) {}
};
class Resection // 后方交汇
{
public:
// 变量部分
double m = 50000; // 比例尺m=50000
double f = 153.24 / 1000; // 焦距f=153.24mm,换算成米
double x0, y0 = 0; // 内方位元素
double phi = 0; // 对应希腊字母fai,三个对应外方位元素的角元素
double w = 0;
double k = 0; // 在竖直摄影情况下,外方位角元素为小角时,可以近似用phi = w = k = 0 求解各个系数
double Xs = 0, Ys = 0, Zs = 0; // 线元素
double m0 = 0; // 单位权中误差
vector imagePoints; // 存储像点
vector terrainPoints; // 存储地面点
int numberP = 0; // 控制点数量
Matrix3d R = Matrix3d::Zero(3,3); // 旋转矩阵
VectorXd L;
MatrixXd A;
VectorXd X;
VectorXd M;
// 函数部分
int PointRead(string path_img, string path_ter); // 读取文件,判断像点数是否等于控制点数,并存储到容器中, 并返回控制点数量
void GetInitialValue(vector terrainPoints, double m, double f, int numberP); // 获取Xs,Ys,Zs,phi,w,k的初值
Matrix3d GetRotateMat(double phi, double w, double k); // 获取旋转矩阵
void GetAL(vector imagePoints, vector terrainPoints, double f, int numberP, Matrix3d R); //得到矩阵A与向量L
bool GetX(MatrixXd A, VectorXd L, int numberP); // 得到改正值x,并判断是否满足结束条件
}; 数据读取
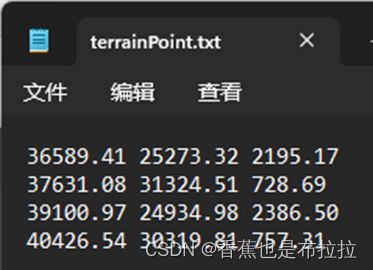
通过 Resection::Pointread( ) 函数实现,将点的坐标按照如下格式存储在txt文件中,输入像点与控制点文件路径,将点读入上面对象中,并返回点数。点坐标格式如下
外方位元素初始化
参考《摄影测量学(第三版)》P63,我们可以得到竖直航空摄影外方位元素初始值确定方法如下:
在代码中,通过 Resection::GetInitialValue( )函数实现,我们通过输入地面点坐标,比例尺,焦距与控制点个数四个变量,可以得到外方位元素初值,并直接赋值在class中。
计算旋转矩阵
参考《摄影测量学(第三版)》P44,我们可以得到矩阵相乘计算公式。
在代码中通过 Resection::GetRotateMat( )函数实现,我们通过输入外方位元素的三个角元素,得到旋转矩阵,并赋值在class中。
计算A与L
参考《摄影测量学(第三版)》P62,对于每一个控制点,其对应A与L计算方式如下:
其中,l代表像点坐标观测值减去利用控制点坐标计算得到的近似值。
在代码中,通过函数 Resection::GetAL( )实现,输入地面点与像点,焦距,点数与旋转矩阵等变量,得到矩阵A与向量L,并直接赋值在class中。
求解X与精度
参考《摄影测量学(第三版)》P62,得到平差公式:
在代码中通过函数 Resection::GetX( )实现,通过输入矩阵A与矩阵L以及点数变量,得到X与各种精度,并直接赋值在class中。函数返回布尔值,当满足结束条件时返回true,其余时返回false。
循环求解
路径选择自己的路径,点的txt文档中数据格式按照上面选取
int main()
{
Resection hyh;
hyh.numberP = hyh.PointRead("C:/Users/86151/Desktop/resection_hyh/imagePoint.txt", "C:/Users/86151/Desktop/resection_hyh/terrainPoint.txt"); // 读取文件
hyh.GetInitialValue(hyh.terrainPoints, hyh.m, hyh.f, hyh.numberP); // 获取初值
int ciridx = 0; // 循环索引,代表循环次数
bool judge = false; // 判断循环是否结束
while (1)
{
if (ciridx == 100)
{
cout << "循环迭代超过100次,我们认为不收敛,停止循环" << endl;
return 0;
}
hyh.R = hyh.GetRotateMat(hyh.phi, hyh.w, hyh.k); // 获取旋转矩阵,class里的矩阵也会发生变化
hyh.GetAL(hyh.imagePoints, hyh.terrainPoints, hyh.f, hyh.numberP, hyh.R); // 得到矩阵A与矩阵L,并复制到class中
judge = hyh.GetX(hyh.A, hyh.L, hyh.numberP); // 得到结果,并计算精度,并将改正值作为下一次循环的初值,计算存储在class中
ciridx++; // 循环次数增加
if (judge == true)
{
cout << "结果满足要求,停止循环,输出结果" << endl;
break;
}
}
cout << fixed << setprecision(5) << "循环迭代了:" << ciridx << "次,结果如下" << endl;
cout << "\tXs=" << hyh.Xs << "\tYs=" << hyh.Ys << "\tZs=" << hyh.Zs << endl;
cout << "\tphi=" << hyh.phi << "\tw=" << hyh.w << "\tk=" << hyh.k << endl;
cout << endl;
cout << "精度分别为:" << endl;
cout << "\tmXs=" << hyh.M(0) << "\tmYs=" << hyh.M(1) << "\tmZs=" << hyh.M(2) << endl;
cout << "\tmphi=" << hyh.M(3) << "\tmw=" << hyh.M(4) << "\tmk=" << hyh.M(5) << endl;
cout << endl;
cout << "单位全中误差m0为:" << hyh.m0 << endl;
cout << endl;
cout << "旋转矩阵R为:" << endl;
cout << hyh.R << endl;
cout << endl;
cout << defaultfloat << "最后一次平差的改正值分别为:" << endl;
cout << setw(10) << left << "\tdXs=" << hyh.X(0) << setw(10) << left << "\tdYs=" << hyh.X(1) << setw(10) << left << "\tdZs=" << hyh.X(2) << endl;
cout << setw(10) << left << "\tdphi=" << hyh.X(3) << setw(10) << left << "\tdw=" << hyh.X(4) << setw(10) << left << "\tdk=" << hyh.X(5) << endl;
return 0;
}总代码
/*
* 空间后方交汇实现
* 参考文献:《摄影测量学(第三版)》 P63
*/
#include
#include
#include
#include
#include
using namespace Eigen;
using namespace std;
#define Restrict1 1e-3
#define Restrict2 1e-6
class imagePoint // 像点,提供数据为毫米,注意单位换算
{
public:
double x;
double y;
imagePoint(double _x, double _y) :x(_x), y(_y) {}
};
class terrainPoint // 地面点,提供数据为米
{
public:
double x;
double y;
double z;
terrainPoint(double _x, double _y, double _z) :x(_x), y(_y), z(_z) {}
};
class Resection // 后方交汇
{
public:
// 变量部分
double m = 50000; // 比例尺m=50000
double f = 153.24 / 1000; // 焦距f=153.24mm,换算成米
double x0, y0 = 0; // 内方位元素
double phi = 0; // 对应希腊字母fai,三个对应外方位元素的角元素
double w = 0;
double k = 0; // 在竖直摄影情况下,外方位角元素为小角时,可以近似用phi = w = k = 0 求解各个系数
double Xs = 0, Ys = 0, Zs = 0; // 线元素
double m0 = 0; // 单位权中误差
vector imagePoints; // 存储像点
vector terrainPoints; // 存储地面点
int numberP = 0; // 控制点数量
Matrix3d R = Matrix3d::Zero(3,3); // 旋转矩阵
VectorXd L;
MatrixXd A;
VectorXd X;
VectorXd M;
// 函数部分
int PointRead(string path_img, string path_ter); // 读取文件,判断像点数是否等于控制点数,并存储到容器中, 并返回控制点数量
void GetInitialValue(vector terrainPoints, double m, double f, int numberP); // 获取Xs,Ys,Zs,phi,w,k的初值
Matrix3d GetRotateMat(double phi, double w, double k); // 获取旋转矩阵
void GetAL(vector imagePoints, vector terrainPoints, double f, int numberP, Matrix3d R); //得到矩阵A与向量L
bool GetX(MatrixXd A, VectorXd L, int numberP); // 得到改正值x,并判断是否满足结束条件
};
int main()
{
Resection hyh;
hyh.numberP = hyh.PointRead("C:/Users/86151/Desktop/resection_hyh/imagePoint.txt", "C:/Users/86151/Desktop/resection_hyh/terrainPoint.txt"); // 读取文件
hyh.GetInitialValue(hyh.terrainPoints, hyh.m, hyh.f, hyh.numberP); // 获取初值
int ciridx = 0; // 循环索引,代表循环次数
bool judge = false; // 判断循环是否结束
while (1)
{
if (ciridx == 100)
{
cout << "循环迭代超过100次,我们认为不收敛,停止循环" << endl;
return 0;
}
hyh.R = hyh.GetRotateMat(hyh.phi, hyh.w, hyh.k); // 获取旋转矩阵,class里的矩阵也会发生变化
hyh.GetAL(hyh.imagePoints, hyh.terrainPoints, hyh.f, hyh.numberP, hyh.R); // 得到矩阵A与矩阵L,并复制到class中
judge = hyh.GetX(hyh.A, hyh.L, hyh.numberP); // 得到结果,并计算精度,并将改正值作为下一次循环的初值,计算存储在class中
ciridx++; // 循环次数增加
if (judge == true)
{
cout << "结果满足要求,停止循环,输出结果" << endl;
break;
}
}
cout << fixed << setprecision(5) << "循环迭代了:" << ciridx << "次,结果如下" << endl;
cout << "\tXs=" << hyh.Xs << "\tYs=" << hyh.Ys << "\tZs=" << hyh.Zs << endl;
cout << "\tphi=" << hyh.phi << "\tw=" << hyh.w << "\tk=" << hyh.k << endl;
cout << endl;
cout << "精度分别为:" << endl;
cout << "\tmXs=" << hyh.M(0) << "\tmYs=" << hyh.M(1) << "\tmZs=" << hyh.M(2) << endl;
cout << "\tmphi=" << hyh.M(3) << "\tmw=" << hyh.M(4) << "\tmk=" << hyh.M(5) << endl;
cout << endl;
cout << "单位全中误差m0为:" << hyh.m0 << endl;
cout << endl;
cout << "旋转矩阵R为:" << endl;
cout << hyh.R << endl;
cout << endl;
cout << defaultfloat << "最后一次平差的改正值分别为:" << endl;
cout << setw(10) << left << "\tdXs=" << hyh.X(0) << setw(10) << left << "\tdYs=" << hyh.X(1) << setw(10) << left << "\tdZs=" << hyh.X(2) << endl;
cout << setw(10) << left << "\tdphi=" << hyh.X(3) << setw(10) << left << "\tdw=" << hyh.X(4) << setw(10) << left << "\tdk=" << hyh.X(5) << endl;
return 0;
}
int Resection::PointRead(string path_img, string path_ter)
{
this->numberP = 0;
// 打开文件
ifstream img(path_img);
ifstream ter(path_ter);
assert(img.is_open() && ter.is_open()); // 确保两个文件都能够打开
double img_x, img_y; // 两个点的坐标
double ter_x, ter_y, ter_z;
while (img >> img_x >> img_y && ter >> ter_x >> ter_y >> ter_z)
{
img_x /= 1000; img_y /= 1000; // 单位换算,随情况变化
this->imagePoints.push_back(imagePoint(img_x, img_y));
this->terrainPoints.push_back(terrainPoint(ter_x, ter_y, ter_z));
this->numberP++;
}
return this->numberP;
}
void Resection::GetInitialValue(vector terrainPoints, double m, double f, int numberP)
{
this->Zs = m * f;
this->Xs = 0; this->Ys = 0;
for (int i = 0; i < numberP; i++)
{
this->Xs += terrainPoints[i].x;
this->Ys += terrainPoints[i].y;
}
this->Xs /= numberP; this->Ys /= numberP;
this->phi = 0; this->w = 0; this->k = 0; // 参考《摄影测量学(第三版)》P61
}
Matrix3d Resection::GetRotateMat(double phi, double w, double k)
{
this->R = Matrix3d::Zero(3, 3);
this->R(0, 0) = cos(phi) * cos(k) - sin(phi) * sin(w) * sin(k);
this->R(0, 1) = -cos(phi) * sin(k) - sin(phi) * sin(w) * cos(k);
this->R(0, 2) = -sin(phi) * cos(w);
this->R(1, 0) = cos(w) * sin(k);
this->R(1, 1) = cos(w) * cos(k);
this->R(1, 2) = -sin(w);
this->R(2, 0) = sin(phi) * cos(k) + cos(phi) * sin(w) * sin(k);
this->R(2, 1) = -sin(phi) * sin(k) + cos(phi) * sin(w) * cos(k);
this->R(2, 2) = cos(phi) * cos(w);
return this->R;
}
void Resection::GetAL(vector imagePoints, vector terrainPoints, double f, int numberP, Matrix3d R)
{
int index = 0;
this->A = MatrixXd::Zero(2 * numberP, 6);
this->L = VectorXd::Zero(2 * numberP);
for (int i = 0; i < numberP; i++)
{
// 对于每一个点,计算其各个值
double Xbar = R(0, 0) * (terrainPoints[i].x - this->Xs) + R(1, 0) * (terrainPoints[i].y - this->Ys) + R(2, 0) * (terrainPoints[i].z - this->Zs);
double Ybar = R(0, 1) * (terrainPoints[i].x - this->Xs) + R(1, 1) * (terrainPoints[i].y - this->Ys) + R(2, 1) * (terrainPoints[i].z - this->Zs);
double Zbar = R(0, 2) * (terrainPoints[i].x - this->Xs) + R(1, 2) * (terrainPoints[i].y - this->Ys) + R(2, 2) * (terrainPoints[i].z - this->Zs);
this->L(index) = imagePoints[i].x + f * Xbar / Zbar;
this->A(index, 0) = (R(0, 0) * f + R(0, 2) * (imagePoints[i].x - this->x0)) / Zbar;
this->A(index, 1) = (R(1, 0) * f + R(1, 2) * (imagePoints[i].x - this->x0)) / Zbar;
this->A(index, 2) = (R(2, 0) * f + R(2, 2) * (imagePoints[i].x - this->x0)) / Zbar;
this->A(index, 3) = (imagePoints[i].y - this->y0) * sin(this->w) - ((imagePoints[i].x - this->x0) / f * ((imagePoints[i].x - this->x0) * cos(this->k) - (imagePoints[i].y - this->y0) * sin(this->k)) + f * cos(this->k)) * cos(this->w);
this->A(index, 4) = -f * sin(this->k) - (imagePoints[i].x - this->x0) / f * ((imagePoints[i].x - this->x0) * sin(this->k) + (imagePoints[i].y - this->y0) * cos(this->k));
this->A(index, 5) = imagePoints[i].y - this->y0;
index++; //对于每一个点,有两行,这一步代表进入第二行
this->L(index) = imagePoints[i].y + f * Ybar / Zbar;
this->A(index, 0) = (R(0, 1) * f + R(0, 2) * (imagePoints[i].y - this->y0)) / Zbar;
this->A(index, 1) = (R(1, 1) * f + R(1, 2) * (imagePoints[i].y - this->y0)) / Zbar;
this->A(index, 2) = (R(2, 1) * f + R(2, 2) * (imagePoints[i].y - this->y0)) / Zbar;
this->A(index, 3) = -(imagePoints[i].x - this->x0) * sin(this->w) - ((imagePoints[i].y - this->y0) / f * ((imagePoints[i].x - this->x0) * cos(this->k) - (imagePoints[i].y - this->y0) * sin(this->k)) - f * sin(this->k)) * cos(this->w);
this->A(index, 4) = -f * cos(this->k) - (imagePoints[i].y - this->y0) / f * ((imagePoints[i].x - this->x0) * sin(this->k) + (imagePoints[i].y - this->y0) * cos(this->k));
this->A(index, 5) = -(imagePoints[i].x - this->x0);
index++; // 索引继续变化,进入下一个点
}
}
bool Resection::GetX(MatrixXd A, VectorXd L, int numberP)
{
VectorXd V = VectorXd::Zero(2 * numberP);
double m0 = 0;
this->X = VectorXd::Zero(6); // 对矩阵进行初始化
this->M = VectorXd::Zero(6);
MatrixXd Q = MatrixXd::Zero(6, 6);
Q = (A.transpose() * A).inverse();
this->X = Q * A.transpose() * L;
V = A * this->X - L;
for (int i = 0; i < numberP; i++)
{
m0 += V(i) * V(i); // 加上vv
}
m0 = sqrt(m0 / (2 * double(numberP) - 6)); // 得到单位权中误差
for (int i = 0; i < 6; i++)
{
this->M(i) = sqrt(Q(i, i)) * m0;
}
this->m0 = m0;
// 将值变为改正值
this->Xs += this->X(0);
this->Ys += this->X(1);
this->Zs += this->X(2);
this->phi += this->X(3);
this->w += this->X(4);
this->k += this->X(5);
// 判断循环是否结束
if (X(0) < Restrict1 && X(1) < Restrict1 && X(2) < Restrict1 && X(3) < Restrict2 && X(4) < Restrict2 && X(5) < Restrict2)
{
return true;
}
else
{
return false;
}
}