整数规划-分支定界法
分支定界法
- 分支定界法由来
- 分支定界法原理
- 分支定界法思想
- 疑惑or改进?
分支定界法由来
谨以此博客作为学习期间的记录
在生活中,整数规划(IP)或者混合整数规划(MIP)往往要比单纯的线性规划(LP)应用更为广泛。生产计划、库存规划等,都有着变量或部分变量为整数的要求。那么对于这些特殊限制(变量为整数),该如何高效求解呢?
在某些特定的条件下,线性规划的最优解为整数解,如下:
m i n c T x s . t . { A x ≥ b x ≥ 0 \begin{align*} min \quad & \mathbf{c}^T \mathbf{x} \\ s.t. \quad & \begin{cases} \mathbf{Ax} \geq \mathbf{b} \\ \mathbf{x} \geq \mathbf{0} \end{cases} \\ \end{align*} mins.t.cTx{Ax≥bx≥0
其中,
- c \mathbf{c} c 是包含目标函数系数的列向量;
- x \mathbf{x} x是决策变量的列向量;
- A \mathbf{A} A是包含约束条件系数的矩阵;
- b \mathbf{b} b是包含约束条件右侧常数的列向量。
在上面的问题中,如果 A A A为幺模矩阵,那么即使不限定x为整数,最终得出的最优解也一定为整数解。
链接: 幺模矩阵-整数解特性
但是在大部分的规划问题中,A都并不满足幺模矩阵,单纯形法可以解决线性规划,但是并不能保证所得出的最优解为整数解,因此就需要一种单独针对整数变量求解的方法。
链接: 单纯形法原理
分支定界法原理
以一个实例介绍分支定界法的流程,实例参考《运筹优化常用模型、算法及案例实战——Python+Java实现》
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x ∈ Z n (整数限制) \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ \mathbf{x} \in \mathbb{Z}^n \quad \text{(整数限制)} \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x∈Zn(整数限制)
可行域绘制如下:
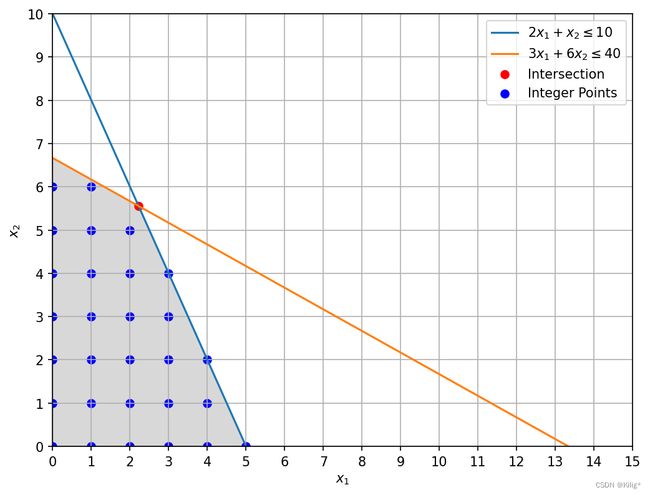
首先忽略 x x x为整数的限制,直接使用单纯形法进行求解。
子问题1:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0
最终解得到
Optimal Objective Value: 1055.5555555555554
x1 = 2.222
x2 = 5.556
将其向下取证,可以得到一个整数解
Optimal Objective Value: 950
x1 = 2
x2 = 5
那么根据求解结果,可以得到结论:最终的目标函数最优值将会介于[950,1055.56)之间。因为在max问题中,即使去掉了整数限制得到的最优值也只有1055.56,如果添加约束最优值只会更低,所以1055.56为目标函数值上界。而目前我们得到整数可行解的目标函数值为950,如果后续求到的解质量非常差,我们也可以把950当为问题的最优解,如果后续有更高质量的解,我们可以将更高质量的解作为最优解。根据当前解得情况,得到根节点。
UB = 1055.56 ,x1 = 2.222,x2 = 5.556
LB = 950,x1 = 2,x2 = 5
由于 x 2 x_2 x2的小数部分更大,为0.556。接下来以 x 2 x_2 x2将原问题进行划分为 x 2 ≤ 5 , x 2 ≥ 6 x_2 \leq 5,x_2\geq 6 x2≤5,x2≥6两部分
子问题2:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≤ 5 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \leq 5 \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≤5
求解得到
Optimal Objective Value: 1000.0
x1 = 2.5
x2 = 5.0
子问题3:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≥ 6 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \geq 6 \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≥6
求解得到
Optimal Objective Value: 1033.3333333333333
x1 = 1.333
x2 = 6.0
由于求解得到的都不是整数解,所以下界(LB)无需更新。而子问题2的当前解小于当前上界,故上界更新。子问题3的当前解小于当前上界,故上界更新。
更新求解树
UB = 1055.56 ,x1 = 2.222,x2 = 5.556
LB = 950,x1 = 2,x2 = 5
UB = 1000.0,x1 = 2.5,x2 = 5.0
LB = 950,x1 = 2,x2 = 5
UB = 1033.33,x1 = 1.333,x2 = 6.0
LB = 950,x1 = 2,x2 = 5
可行域划分如下

由于子问题3的上界大于子问题2的上界。那么可以假设子问题3具有更大的潜力,因此优先从子问题3开始搜索。
由于子问题3中 x 1 x_1 x1的小数部分更大,为0.333。接下来以 x 1 x_1 x1将原问题进行划分为 x 1 ≤ 1 , x 2 ≥ 2 x_1 \leq 1,x_2\geq 2 x1≤1,x2≥2两部分
子问题4:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≥ 6 x 1 ≤ 1 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \geq 6 \\ x_1 \leq 1 \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≥6x1≤1
求解得到
Optimal Objective Value: 1025.0
x1 = 1.0
x2 = 6.167
子问题5:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≥ 6 x 1 ≥ 2 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \geq 6 \\ x_1 \geq 2 \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≥6x1≥2
求解得到
Infeasible or unbounded model
子问题5不可行。
由于求解得到的都不是整数解,所以下界(LB)无需更新。而子问题4的当前解小于当前上界,故上界更新。
更新求解树
UB = 1055.56 ,x1 = 2.222,x2 = 5.556
LB = 950,x1 = 2,x2 = 5
UB = 1000.0,x1 = 2.5,x2 = 5.0
LB = 950,x1 = 2,x2 = 5
UB = 1033.33,x1 = 1.333,x2 = 6.0
LB = 950,x1 = 2,x2 = 5
UB = 1025.0,x1 = 1.0,x2 = 6.167
LB = 950,x1 = 2,x2 = 5
只能从子问题4开始搜索了,继续划分为 x 2 ≤ 6 , x 2 ≥ 7 x_2 \leq 6,x_2 \geq 7 x2≤6,x2≥7
子问题6:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≥ 6 x 1 ≤ 1 x 2 ≤ 6 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \geq 6 \\ x_1 \leq 1\\ x_2 \leq 6 \\ \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≥6x1≤1x2≤6
求解得到
Optimal Objective Value: 1000.0
x1 = 1.0
x2 = 6.0
子问题7:
m a x z = 100 x 1 + 150 x 2 s . t . { 2 x 1 + x 2 ≤ 10 3 x 1 + 6 x 2 ≤ 40 x 1 , x 2 ≥ 0 x 2 ≥ 6 x 1 ≤ 1 x 2 ≥ 7 \begin{align*} max \quad &z = 100x_1 + 150x_2 \\ s.t. \quad & \begin{cases} 2x_1+x_2 \leq 10 \\ 3x_1+6x_2 \leq 40 \\ x_1,x_2 \geq 0\\ x_2 \geq 6 \\ x_1 \leq 1\\ x_2 \geq 7 \\ \end{cases} \\ \end{align*} maxs.t.z=100x1+150x2⎩ ⎨ ⎧2x1+x2≤103x1+6x2≤40x1,x2≥0x2≥6x1≤1x2≥7
求解得到
Infeasible or unbounded model
模型无解。
由于子问题6得出了整数解,且整数解大于下界,因此上界下界同时更新。
更新之后的求解树如下:
UB = 1055.56 ,x1 = 2.222,x2 = 5.556
LB = 950,x1 = 2,x2 = 5
UB = 1000.0,x1 = 2.5,x2 = 5.0
LB = 950,x1 = 2,x2 = 5
UB = 1033.33,x1 = 1.333,x2 = 6.0
LB = 950,x1 = 2,x2 = 5
UB = 1025.0,x1 = 1.0,x2 = 6.167
LB = 950,x1 = 2,x2 = 5
UB = 1000.0,x1 = 1.0,x2 = 6.0
LB =1000.0,x1 = 1.0,x2 = 6.0
此时子问题6的上界等于下界,算法收敛,退出。
最优解如下:
Optimal Objective Value: 1000.0
x1 = 1.0
x2 = 6.0
那么,还有一个问题。就这样结束了吗?子问题2还没有进行搜索,就可以确定子问题6的解为原问题最优解了吗?
答: 子问题2无需再搜索了,子问题2当前UB为1000,继续往下搜索,增加约束,UB只会越来越低,因此子问题2的孩子节点不可能再有解>1000的情况,因此可以确定子问题6得出的解即为最优解。
分支定界法思想
分支定界法的核心思想有以下几部分
- 对可行域的划分,根据当前非整数解划分解空间
- 剪枝策略
疑惑or改进?
在子问题中,如果将求解得到的非整数解向下取整,若可行,同样可以更新下界。这样上界和下界同时更新,模型可以更快收敛。为什么没有这样做呢?
上述用到的代码链接