python实现图像的几何变换——冈萨雷斯数字图像处理
1、 实现图像的平移。
原理:
图像的平移是一种基本的图像处理操作,它将图像中的每个像素沿着指定的方向和距离移动,以创建一个新的平移后的图像。平移的原理很简单,通常涉及到以下几个步骤:
-
确定平移的距离和方向:首先,确定您希望将图像沿着哪个方向移动以及移动多远。这可以通过定义一个平移向量来实现,该向量包含了水平和垂直方向上的移动距离。
-
创建一个新的图像:为了执行平移操作,您需要创建一个与原始图像相同大小的新图像,通常称为目标图像。这个目标图像将用于存储平移后的图像。
-
遍历原始图像的像素:对于原始图像中的每个像素,将其从原始图像中取出。
-
计算新的像素位置:对于每个取出的像素,根据平移向量的值计算其在目标图像中的新位置。通常,新位置的计算方法如下:
新X坐标 = 原X坐标 + 水平平移距离
新Y坐标 = 原Y坐标 + 垂直平移距离 -
将像素放置到目标图像中:将每个像素放置到目标图像的新位置上。如果新位置超出了目标图像的边界,可以选择丢弃该像素或采用某种插值方法来填充。
重复步骤3至步骤5:重复以上步骤,直到遍历了原始图像的所有像素。
完成平移操作:完成后,目标图像就包含了原始图像沿指定方向平移后的图像。
在这里,我们采用OpenCV的warpAffine函数来解决图像平移,cv2.warpAffine 是 OpenCV(Open Source Computer Vision Library)中的一个函数,用于执行仿射变换(Affine Transformation)操作。仿射变换是一种线性变换,它可以用来实现图像的平移、旋转、缩放、剪切等操作。该函数的主要作用是将输入图像应用一个仿射变换矩阵,从而生成一个经过变换的输出图像。通常,可以使用这个函数来实现图像的平移、旋转、缩放和剪切等操作,而不需要手动编写复杂的像素级操作。
以下是 cv2.warpAffine 函数的一般用法:
cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])
src:输入图像。
M:仿射变换矩阵,用于指定要执行的变换操作。
dsize:输出图像的大小。
dst(可选):输出图像。如果未提供,则函数会创建一个新的图像。
flags(可选):插值方法的标志,用于确定如何处理像素之间的插值。
borderMode(可选):图像边界像素的处理方式,通常用于变换后的图像可能超出原始图像边界的情况。
borderValue(可选):用于边界填充的像素值。
编写代码,输出如下图所示的结果:

如果(x,y)方向的平移量分别为(t_x, t_y),则变换矩阵

可以用类型为np.float32的numpy数组来表示它,并将其作为参数传给cv2.warpAffine函数完成几何变换。上图中

代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena_gray_512.tif")
rows,cols,channel=img.shape
affineShrink = np.array([[1,0,100],[0,1,50]],np.float32)
shrinkTwoTimes = cv2.warpAffine(img, affineShrink, (cols, rows), borderValue=10)
plt.subplot(121),plt.imshow(img,'gray'),plt.title("original")
plt.subplot(122),plt.imshow(shrinkTwoTimes,'gray'),plt.title("translation")
plt.show()
cv2.waitKey(0)
cv2.destroyAllWindows()
结果展示
2、实现图像的旋转
原理
图像旋转是数字图像处理中的一项基本操作,它的原理可以分为几个关键步骤:
**定义旋转中心:**通常旋转是围绕图像的某一点进行的。这个点可以是图像的中心,也可以是任意一点。
旋转变换:在二维空间中,旋转可以通过旋转矩阵来实现。对于一个给定的旋转角度θ,旋转矩阵是这样的:

这个矩阵可以用来计算图像中每个像素旋转后的新位置。
像素映射:在旋转图像时,原始图像中的像素需要映射到新的位置。这通常涉及插值算法,如最近邻插值、双线性插值或三次样条插值,以确定新位置的像素值。
处理边界问题:旋转后,图像可能会超出原始图像的边界。这可能需要对图像进行裁剪或填充。
反走样:由于旋转可能导致像素不再对齐,因此可能需要进行反走样处理以减少锯齿效应。
但是在OpenCV 允许在任意地方进行旋转,这里旋转矩阵的形式应该修改为

为了构建这个旋转矩阵,OpenCV 提供了一个函数:cv2.getRotationMatrix2D。
编写代码,输出如下图所示的结果:
提示:
可以先用函数cv2.getRotationMatrix2D得到变换矩阵,该函数的参数包括:旋转中心坐标、旋转角度等,所以利用该函数可以实现围绕任意中心的旋转;旋转角度为正表示逆时针旋转。之后将得到的变换矩阵作为参数传给cv2.warpAffine函数完成几何变换。上图中旋转中心为图像中心,旋转角度为45°。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread('lena_gray_512.tif',0)
rows,cols=img.shape
# 这里的第一个参数为旋转中心,第二个为旋转角度,第三个为旋转后的缩放因子
# 可以通过设置旋转中心,缩放因子,以及窗口大小来防止旋转后超出边界的问题
M=cv2.getRotationMatrix2D((cols/2,rows/2),45,1)
# 第三个参数是输出图像的尺寸中心
dst=cv2.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img,'gray'),plt.title("original")
plt.subplot(122),plt.imshow(dst,'gray'),plt.title("rotation")
plt.show()
cv2.destroyAllWindows()
结果展示
3、 实现图像的缩放
原理
图像缩放是数字图像处理中的一项重要技术,它涉及改变图像的尺寸,包括放大和缩小。主要流程如下
**定义缩放比例:**首先确定缩放的比例。这个比例可以是均匀的(横向和纵向相同)或不均匀的(横向和纵向不同)。
**计算新像素位置:**根据缩放比例,为原始图像中的每个像素计算在缩放后图像中的新位置。如果是放大图像,新图像中的许多像素位置将没有直接对应的原始像素;如果是缩小图像,一些原始像素将不会在新图像中有对应位置。
**像素插值:**由于缩放过程中新像素位置可能并不对应原始图像中的确切像素,因此需要通过插值算法来确定这些新位置的像素值。常见的插值方法包括:
**最近邻插值:**将新像素的值设置为最接近的原始像素值。这种方法简单快速,但可能导致图像走样。
双线性插值:考虑最接近的四个像素,通过线性插值计算新像素值。这种方法在图像质量和计算复杂度之间提供了一个较好的平衡。
**双三次插值:**考虑最接近的16个像素,使用三次插值算法计算新像素值。这种方法可以提供更高质量的结果,但计算更为复杂。
**处理边界问题:**在缩放过程中,新图像的尺寸可能与原始图像不完全相符,特别是在不均匀缩放的情况下。这可能需要对图像进行裁剪或填充。
**质量控制:**图像缩放可能会引入各种失真,如锯齿效应或模糊。因此,可能需要采用附加的图像处理技术来优化结果,如锐化处理或反走样技术。
实现下图显示的结果
提示
用函数cv2.resize对图像进行8倍放大,参数分别为cv2.INTER_NEAREST、cv2.INTER_LINEAR和cv2.INTER_CUBIC时代表选择最近邻插值法、双线性插值法、三次样条插值法。
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
img=cv.imread("jellybeans.png")
img= cv.cvtColor(img,cv.COLOR_RGB2GRAY)
print(img.shape)
x, y = img.shape[0:2]
near = cv.resize(img,(0,0), fx=8, fy=8,interpolation=cv.INTER_NEAREST)
linear= cv.resize(img, (0,0), fx=8, fy=8,interpolation=cv.INTER_LINEAR)
cubic=cv.resize(img, (0,0), fx=8, fy=8,interpolation=cv.INTER_CUBIC)
plt.subplot(221),plt.imshow(img,'gray'),plt.title("original")
plt.subplot(222),plt.imshow(near,'gray'),plt.title("nearest")
plt.subplot(223),plt.imshow(linear,'gray'),plt.title("linear")
plt.subplot(224),plt.imshow(cubic,'gray'),plt.title("cubic")
plt.show()
结果展示
import cv2
import numpy as np
import matplotlib.pyplot as plt
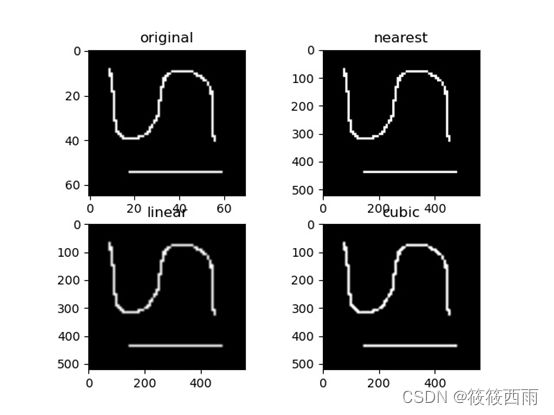
img=cv2.imread("binarysmall.png")
img=cv2.cvtColor(img,cv2.COLOR_RGV2GRAY)
print(img.shape)
x,y=img.shape[0:2]
near=cv2.resize(img,(0,0),fx=8,fy=8,interpolation=cv2.INTER_NEAREST)
linear=cv2.resize(img,(0,0),fx=8,fy=8,interpolation=cv2.INTER_LINEAR)
cubic=cv2.resize(img,(0,0),fx=8,fy=8,interpolation=cv2.INTER_CUBIC)
plt.subplot(221),plt.imshow(img,"gray"),plt.title("original")
plt.subplot(222),plt.imshow(near,"gray"),plt.title("nearst")
plt.subplot(223),plt.imshow(linear,"gray"),plt.title("linear")
plt.subplot(224),plt.imshow(cubic,"gray"),plt.title("cubic")
plt.show()
结果展示
结果分析
INTER_NEAREST - 最近邻插值
根据名字也知道,这是插入的数值采用与原图像最近的那个点的数值,这种方法比较简单,但是人为痕迹有点重。
插值后的边缘效果:由于是以最近的点作为新的插入点,因此边缘不会出现缓慢的渐慢过度区域,这也导致放大的图像容易出现锯齿的现象
INTER_LINEAR - 线性插值

比如插值点为(x,y),这个像素是由围着他的4个点的像素决定的,
先求得:
f(x,0)=f(0,0)+x[f(1,0)-f(0,0)]
f(x,1)=f(0,1)+x[f(1,1)-f(0,1)]
在对求得值做一次线性插值:
f(x,y)=f(x,0)+y[f(x,1)-f(x,0)]
即可。这个准确的说是双线性
插值后的边缘效果:可以有效避免出现锯齿的现象
INTER_CUBIC –三次样条插值
基本的原理跟线性插值类似,都是做完一个方向再做另一个,不过他是用4*4的像素来计算的,但是在求权的时候不是线性的,而是逼近sin(x)/x:

插值后的边缘效果:可以有效避免出现锯齿的现象
总的来说,最近邻插值会出现锯齿现象,导致图片变形,感觉不太好。