【数据结构入门精讲 | 第八篇】一文讲清全部排序算法（2）

在上一篇文章中我们介绍了冒泡排序、快速排序等算法，这一篇我们接着对排序算法的学习。

归并排序

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

• 归并排序的时间复杂度始终为O(nlogn)，但需要额外的空间来存储临时数组。空间复杂度为O(n)

代码

#include 

// 合并两个有序数组
void merge(int arr[], int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
    int L[n1], R[n2];

    // 将元素复制到临时数组L和R中
    for (int i = 0; i < n1; i++) {
        L[i] = arr[left + i];
    }
    for (int j = 0; j < n2; j++) {
        R[j] = arr[mid + 1 + j];
    }

    // 合并临时数组L和R到arr
    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // 将剩余的元素复制到arr中
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// 归并排序函数
void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;

        // 递归地对左右两个子数组进行排序
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);

        // 合并两个有序数组
        merge(arr, left, mid, right);
    }
}

// 测试归并排序算法
int main() {
    int arr[] = {5, 2, 9, 4, 7, 6, 1, 3, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    mergeSort(arr, 0, n - 1);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序的时间复杂度为O(nlogn)，空间复杂度为O(1)

堆排序的特点：可以左子树大右子树小，也可以左子树小右子树大；当父节点比孩子节点都大时，称为大根堆；相反的，称为小根堆

举个例子：如何对33 29 44 37 21进行堆排序呢？
先按层次写为
     33
  29    44
37  21


并且编号
         33(0)
    29(1)    44(2)
37(3)  21(4)


接着把n/2-1对应的编号找出来（可以向下取整）
即5/2-1等于1
1对应29，所以对29进行处理
29 37 21三者，将37与29替换
得到
         33(0)
    37(1)    44(2)
29(3)  21(4)


接着将指针减一，即此时对编号为0的进行处理
得到
         44(0)
    37(1)    33(2)
29(3)  21(4)

如何在这个堆中插入66呢？
         44(0)
    37(1)    33(2)
29(3)  21(4)
先把66放在最后的节点
         44(0)
    37(1)      33(2)
29(3)  21(4)  66
由于这个树本来就是排序好的，因此现在只需要排序66以及它的祖先节点，即66 33 44


那么如何删去一个节点呢？
把最后一个节点放到该删去的节点上
比如要删掉44，就把66替换44
         66(0)
    37(1)      33(2)
29(3)  21(4)
之后再进行排序即可

---

堆中还有两个概念
小根堆：树中父亲都比孩子小的堆。
大根堆：树中父亲都比孩子大的堆。

如何构成小根堆、大根堆呢？

如何将46 79 56 38 40 84构成小根堆
先层次遍历
得到
      46
   79    56
 38 40  84
接着观察后两层，38、79、40中38最小，所以38和79互换


      46
   38    56
 79 40  84
 后两层没有大小关系之后，将上面两层进行比较
 38、46、56中38小，所以38与46互换
 
      38
   46    56
 79 40  84
互换完成后再观察一遍发现46、40、79中40最小，所以40与46互换
      38
   40    56
 79 46  84
 这样就得到了小根堆
 大根堆的排序也是类似的

例题：

插入5，2，7，3，4，1，6使之成为最小堆，则层次遍历完再进行处理

解法：
先层次遍历
       5
     2  7
   3 4 1 6
由于7、1、6不是小根堆
所以变为
       5
     2  1
   3 4 7 6
由于5、1、2不是小根堆
所以变为
       1
     2  5
   3 4 7 6
此时前序遍历的结果就是1 2 3 4 5 7 6

代码

#include 

// 交换两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 调整堆，使其满足堆的性质
void heapify(int arr[], int n, int i) {
    int largest = i;         // 初始化根节点为最大值
    int left = 2 * i + 1;    // 左子节点位置
    int right = 2 * i + 2;   // 右子节点位置

    // 如果左子节点比根节点大，则更新最大值位置
    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }

    // 如果右子节点比最大值位置对应的节点值大，则更新最大值位置
    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    // 如果最大值位置不是根节点，则进行交换，并递归调整子堆
    if (largest != i) {
        swap(&arr[i], &arr[largest]);
        heapify(arr, n, largest);
    }
}

// 堆排序函数
void heapSort(int arr[], int n) {
    // 建堆，从最后一个非叶子节点开始调整，直到根节点
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // 逐个将堆顶元素（最大值）放到已排序部分的末尾，并调整堆
    for (int i = n - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);   // 将堆顶元素与最后一个元素交换
        heapify(arr, i, 0);       // 调整堆
    }
}

// 测试堆排序算法
int main() {
    int arr[] = {5, 2, 9, 4, 7, 6, 1, 3, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    heapSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

选择排序

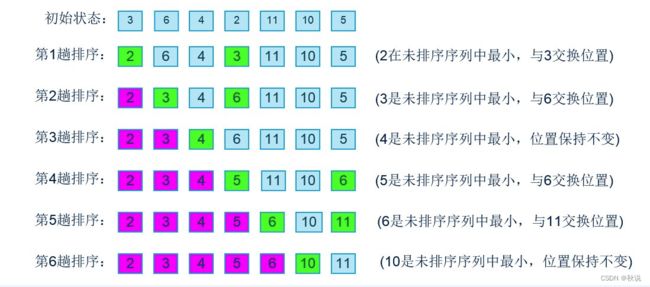
选择排序是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

代码

#include 

// 交换两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 选择排序函数
void selectionSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int min_index = i;

        // 找到未排序部分的最小元素索引
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }

        // 将最小元素与未排序部分的第一个元素交换位置
        swap(&arr[min_index], &arr[i]);
    }
}

// 测试选择排序算法
int main() {
    int arr[] = {5, 2, 9, 4, 7, 6, 1, 3, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    selectionSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

计数排序

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法，而且当O(k)＞O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n))，如归并排序，堆排序）

基本步骤：

1.找到待排序数组中的最大值max和最小值min，确定计数数组的长度为(max - min + 1)。
2.创建一个计数数组count，长度为max - min + 1，并将所有元素初始化为0。
3.遍历待排序数组，统计每个元素出现的次数，将对应计数数组的元素加1。
4.对计数数组进行累加操作，使得每个元素表示的是小于等于当前元素的元素总数。
5.创建一个临时数组output，长度与待排序数组相同。
6.从待排序数组末尾开始遍历，将每个元素放到output数组中的正确位置上，同时将计数数组中对应元素的值减1。
7.将output数组复制回原始数组，完成排序过程。

计数排序的时间复杂度为O(n+k)，其中n是待排序数组的长度，k是待排序元素的取值范围大小。需要注意的是，计数排序是一种稳定的排序算法，但是它的空间复杂度较高，取决于元素的取值范围。

代码

#include 
#include 

// 计算数组中的最大值
int getMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }
    return max;
}

// 计数排序函数
void countingSort(int arr[], int n) {
    int max = getMax(arr, n);
    int* count = (int*)calloc(max + 1, sizeof(int));  // 申请计数数组，初始化为0
    for (int i = 0; i < n; i++) {
        count[arr[i]]++;   // 统计每个元素出现的次数
    }
    for (int i = 1; i <= max; i++) {
        count[i] += count[i - 1];   // 累加计数数组，得到每个元素在排序后序列中的位置
    }
    int* output = (int*)malloc(n * sizeof(int));   // 申请临时输出数组
    for (int i = n - 1; i >= 0; i--) {
        output[count[arr[i]] - 1] = arr[i];   // 将元素放到对应位置
        count[arr[i]]--;   // 将计数数组中对应元素的值减1
    }
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];   // 将临时输出数组复制回原数组
    }
    free(count);   // 释放计数数组所占用的空间
    free(output);  // 释放临时输出数组所占用的空间
}

// 测试计数排序算法
int main() {
    int arr[] = {5, 2, 9, 4, 7, 6, 1, 3, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    countingSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

基数排序

基数排序是非比较型整数排序算法,其原理是将整数按位分割进行排序。基数排序适用于大范围数据排序,打破了计数排序的限制。

基本步骤：

找到待排序数组中最大元素max的位数d，即max的十进制位数。
从最低位开始，对待排序数组中的每一位进行排序，直到最高位。
对于每一位，创建10个桶，分别用来存储该位上为0~9的元素。
将待排序数组中的元素按照当前位的值放入对应的桶中。
依次将每个桶中的元素收集起来，得到一个新的待排序数组。
重复步骤4~5，直到所有位都被排序完成。

代码

#include 

// 获取数字 num 的第 d 位数字
int getDigit(int num, int d) {
    int divisor = 1;
    for (int i = 0; i < d; i++) {
        divisor *= 10;
    }
    return (num / divisor) % 10;
}

// 基数排序函数
void radixSort(int arr[], int n) {
    // 找到最大值
    int maxVal = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > maxVal) {
            maxVal = arr[i];
        }
    }

    // 计算位数
    int digit = 0;
    while (maxVal > 0) {
        maxVal /= 10;
        digit++;
    }

    // 创建 10 个桶
    int bucket[10][n];
    int count[10] = {0};

    // 按位进行分配和收集
    for (int d = 0; d < digit; d++) {
        // 分配
        for (int i = 0; i < n; i++) {
            int num = arr[i];
            int index = getDigit(num, d);
            bucket[index][count[index]] = num;
            count[index]++;
        }

        // 收集
        int k = 0;
        for (int i = 0; i < 10; i++) {
            for (int j = 0; j < count[i]; j++) {
                arr[k] = bucket[i][j];
                k++;
            }
            count[i] = 0;  // 清空计数器
        }
    }
}

// 测试基数排序算法
int main() {
    int arr[] = {53, 3, 542, 748, 14, 214, 154, 63, 616};
    int n = sizeof(arr) / sizeof(arr[0]);

    radixSort(arr, n);

    printf("Sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");

    return 0;
}

排序总结

冒泡排序、起泡排序	O(n^2)	比较次数：n*(n-1)/2	稳定	空间O(1)
插入排序	最优（有序）O(n) 最坏（逆序）O(n^2)		稳定	空间O(1)
希尔排序	O(nlong)~O(n^2)		不稳定	空间O(1)
快速排序	平均、最好O(nlong) 最坏O(n^2)		不稳定	空间O(logn)
桶排序	O(n)		稳定	空间O(n)
归并排序	O(nlogn)	归并趟数的数量级：O(logn)	稳定	空间O(n)
堆排序	O(nlogn)		不稳定	空间O(1)
选择排序	O(n^2)	比较次数：O(n^2) 移动次数：O(N)	不稳定	空间O(1)
计数排序	O(n)		稳定
基数排序	O(n)		稳定	空间O(n)

至此，排序算法的相关知识点就以及介绍完毕了，接下来我们将进行排序算法知识点的相关练习。