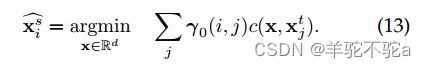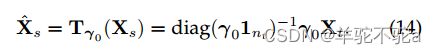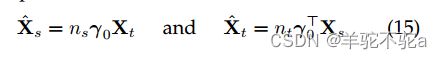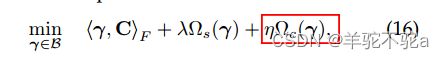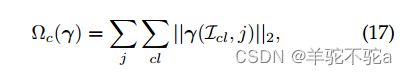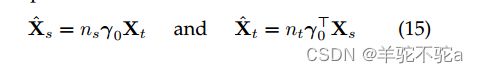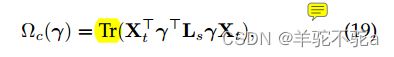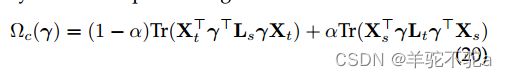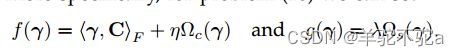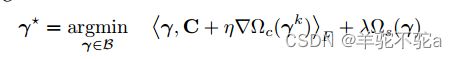【最优传输论文笔记一】Optimal Transport for Domain Adaptation

前言

在本文中，提出了一个正则化的无监督最优传输模型来执行源域和目标域的表示对齐。学习了一个匹配两个概率密度函数（PDF）的传输计划，它约束源域中同一类的标记样本在传输过程中保持接近。这样，我们同时利用源中的标记样本和在两个域中观察到的分布。

1.introduce

一些理论工作强调了域的数据概率分布函数之间的散度所起的作用。因此文章提出了符合最少努力原则的源数据转换，即相对于转换成本或度量的影响最小。从这个意义上说，自适应问题归结为:i)找到匹配源和目标分布的输入数据的转换，然后ii)从转换后的源样本中学习一个新的分类器。这个过程如图1所示。在本文中，我们提倡一种基于最优传输的解决方案来寻找这种转换。并引入了一种新的无监督域适应框架，包括基于经验观察的最优运输学习。此外，我们提出了几个正则化术语，它们既可以编码源域中包含的类信息，也可以促进邻域结构的保存。提出了一种求解正则化最优运输优化问题的有效算法。最后，通过在最优传输优化问题中进行简单而优雅的修改，该框架也可以很容易地扩展到目标域中可用标签很少的半监督情况。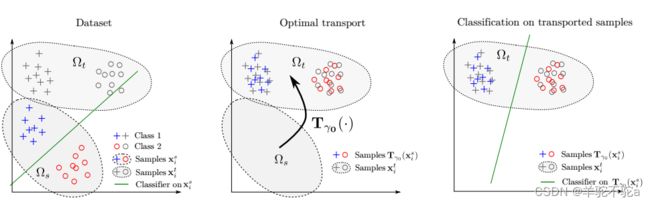

Domain adaptation：域适应策略可以大致分为两类，这取决于它们是否假设目标域(半监督DA)中存在少量标签(无监督DA)。

其中半监督自适应主要方法：使用源样本和变换后的目标样本之间的内积来搜索在两个域中都有区别的投影。学习投影，其中目标域的标记样本落在源数据上训练的大边缘分类器的正确一侧。一些基于成对约束下共同特征提取的工作也被引入作为领域自适应策略。

无监督领域自适应：可以考虑样本重新加权、为两个域找到共同的特征表示。例如：匹配特征空间中的域的均值、通过域的相关性对齐域或通过使用成对约束来执行自适应。

文中的方法为源域中的每个样本定义了局部变换，可以视为一个图匹配问题。每个源样本都必须在边际分布保持的约束下映射到目标样本上。

2.最优传输和应用领域适应

大多数域自适应方法通常会做出以下两个假设中的至少一个:

类不平衡:两个域的标签分布是不同的，但样本关于标签的条件分布是相同的;

协变量移位:标签相对于数据的条件分布是相等的，或等效的。然而，两个域的数据分布应该是不同的。为了使适应技术有效，这种差异需要很小。

在实际应用程序中，源域和目标域之间发生的漂移通常意味着边际分布和条件分布的变化。

在我们的工作中，我们假设域漂移是由于输入空间T: Ωs→Ωt的一个未知的，可能是非线性的变换。我们假设转换保留了条件分布，即:.这意味着变换保留了标签信息，贝叶斯决策函数通过方程联系起来。

3.正则离散最优传输

基于OT的样本映射:源样本的变换可以方便地表示为对目标样本的以下重心映射:

其中是给定的源样本，是其对应的图像。当代价函数是squared 距离时，这个重心对应一个加权平均值，样本被映射到目标样本的凸包中。因此，对于所有源样本，这种重心映射可以表示为:

当边缘µs和µt是均匀的时，可以很容易地将重心映射导出为线性表达式:

4.用于领域自适应的类正则化

在本节中，我们探讨了在运输过程中保留标签信息和样本邻域的正则化术语。最后，我们讨论了半监督的情况，并表明目标域中的标签信息可以有效地包含在所提出的模型中。

4.1使用分类标签正则化运输

我们的目标是惩罚将具有不同标签的源样本匹配到相同目标样本的耦合。为此，我们建议在正则化最优运输中添加一个新的术语，从而导致以下优化问题：

其中η≥0且是一个基于类的正则化项。 

 在这项工作中，我们提出并研究了正则化子的两种选择。第一种是基于群稀疏性，并促进概率耦合γ0，其中给定的目标样本从具有相同标签的源样本接收质量。第二种是基于图拉普拉斯正则化，并在源传输样本中促进了局部光滑和类规则的结构。

4.1.1具有群稀疏性的正则化

在本文中，我们保留了基本问题的凸性，并使用凸群套索正则化子。这个正则化子定义为

 

 其中||·||2表示范数，包含中与类的源域样本相关的行的索引。因此，是一个向量，包含与类相关的的第j列的系数。由于的第j列与第j个目标样本相关，该正则化子将在目标样本中引入所需的稀疏表示。

理想情况下，使用该正则化子，我们期望与每组标签相对应的质量是源域和目标域的唯一匹配样本。因此，为了使域自适应问题具有相关的解决方案，期望在源分布和目标分布中都保留标签的分布。因此，我们需要。

 4.1.2拉普拉斯正则化

该正则化术语旨在在传输过程中保留数据结构（用图近似)。直观地说，我们希望源域中的相似样本在运输后也相似。因此，通过方程将传输的源样本表示为，其中线性依赖于传输矩阵。现在，给定源域中样本的正对称相似性矩阵Ss，我们的正则化项定义为:

 其中是编码源样本对之间相似性的矩阵的系数。为了进一步保留类结构，我们可以稀疏不同类的样本的相似性。因此，在实践中，如果，则我们强制。

当边际分布是均匀的时，上述方程可以被简化。在这种情况下，可以根据等式

来计算传输的源样本。因此归结为

Tr：对角线元素之和 称为矩阵的迹

其中是图的拉普拉斯算子。因此正则化子是二次型w.r.t。即将式子（18）中的相似度矩阵换成图拉普拉斯矩阵。||·||二次型用式子（15）替换。

正则化项（18）或（19）是基于传输的源样本来定义的。当相似性信息在目标样本中也可用时，例如，通过相似性矩阵，我们可以利用这一知识和形式的对称拉普拉斯正则化

与矩阵不同，相似性矩阵不能根据类结构稀疏化，因为标签通常不可用于目标域。  

用于图像之间的直方图自适应。然而，作者关注的是位移，而不是保留传输样本的类结构。

 4.2半监督域自适应的正则化

在半监督域自适应中，目标域中几乎没有可用的标记样本。同样，这样一个重要的信息可以通过一个新的正则化项来利用，该正则化项将被集成到原始的最优传输公式中。该正则化项被设计为使得目标域中的样本应该仅与源域中具有相同标签的样本匹配。可以表示为：

 

其中M是代价矩阵，当（或j是具有未知标签的样本）时，，否则为+∞。这个术语的优点是不含参数。它可以归结为通过向不期望的匹配添加无限成本来改变方程（8）中定义的原始成本函数C。例如，可以通过使用目标样本属于类的概率置信度来设计这种正则化的平滑版本。但我们在这项工作中并没有探讨后一种选择。同样值得注意的是，方程（20）中的拉普拉斯策略也可以通过矩阵的定义来利用目标域中的这些类标签。

 5.半监督域自适应的正则化

在这项工作中，我们的目标是一种更具可扩展性的算法。为此，我们考虑了一种基于条件梯度算法[7]的泛化的方法，称为广义条件梯度（GCG）。GCG算法的框架解决了组合函数的约束最小化的一般情况，定义为

 

其中f（·）是一个可微且可能是非凸函数；g（·）是一个凸的，可能不可微的函数；B表示的任何凸子集和紧子集。如算法1所示，除了搜索方向部分（第3行）外，GCG算法的所有步骤与用于CG的步骤完全相同。不同之处在于，GCG只线性化了复合目标函数的f（·）部分，而不是整个目标函数。更具体地说，对于问题（16），我们可以设置

 

现在假设是可微的，算法1的步骤3归结为 

 

总结

在本文中，描述了一种基于最优传输的新框架来解决无监督领域自适应问题。我们提出了两种正则化方案来在运输计划的估计过程中对源域中的类结构进行编码，从而强化了同一类的样本必须经历类似变换。并将这种OT正则化框架扩展到半监督域自适应情况，即目标域中几乎没有标签可用的情况。

关于计算方面，建议使用条件梯度算法的修改版本，即广义条件梯度分裂，这使该方法能够扩展到真实世界的数据集。最后，我们将所提出的方法应用于合成数据集和现实世界数据集。结果表明，最优运输领域自适应方案往往优于竞争的最先进的方法。