层次分析法
层次分析法主要用于解决评价类问题(例如选择哪种方案最好，哪位运动员或者员工表现的更优秀)
先用一道引出层次分析法的例题：小明同学高考填完志愿后，小明想出去旅游。在查阅了网上的攻略后，他初步选择了苏杭、北戴河和桂林三地之一作为目标景点。请你确定评价指标体系、形成评价体系来为小明同学选择最佳的方案。
对于评价类问题，我们首先应该想到以下三个问题：
（1）我们评价的目标是什么？
为小明同学选择最佳的旅游景点
（2）我们为了达到这个目标有哪几种可选的方案？
三种，分别是去苏杭、去北戴河和去桂林
（3）评价的准则或者说指标是什么?（我们根据什么东西来评价好坏)
题目没给相关数据支撑，需要我们确定一般而言，前两个问题的答案是显而易见的，第三个问题的答案需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合，从中筛选出最合适的指标。网上优先选择知网（或者万方、百度学术、谷歌学术等平台)搜索相关的文献
在写论文的时候如果引用专家的文章会显得很专业哦。
假如我们查询了资料后选择了以下五个指标：
景点景色
旅游花费
居住环境
饮食情况
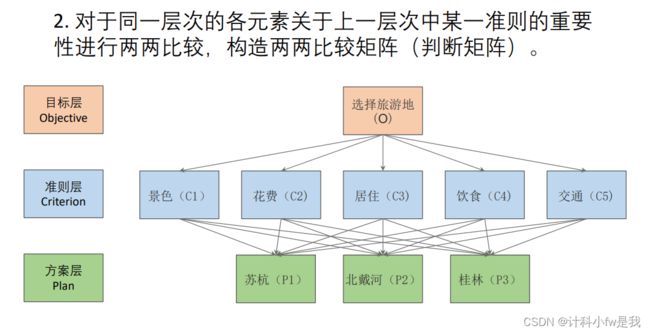
交通便利程度我们对小明怎么提问才能帮他合理的做决定呢？有这样一张表格：
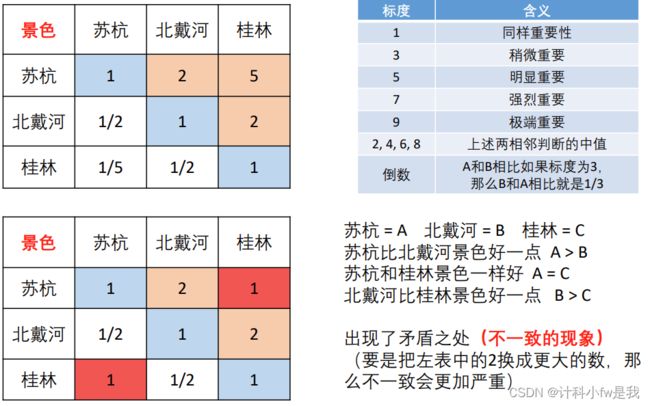
有的同学会说直接让小明填好这张表不就好了？不不不，这样往往比较片面，如果明天再让他填一次，大概率就不一样了，引用这样一段话：
在确定影响某因素的诸因子在该因素中所占的比重时，遇到的主要困难
是这些比重常常不易定量化。此外，当影响某因素的因子较多时，直接
考虑各因子对该因素有多大程度的影响时，常常会因考虑不周全、顾此
失彼而使决策者提出与他实际认为的重要性程度不相一致的数据，甚至
有可能提出一组隐含矛盾的数据。
——选自司守奎老师的《数学建模算法与应用》我们的问题是一次性考虑这五个指标之间的关系，往往考虑不周，解决方法就是两个两个指标进行比较，最终根据两两比较的结果来推算出权重
基本思想：
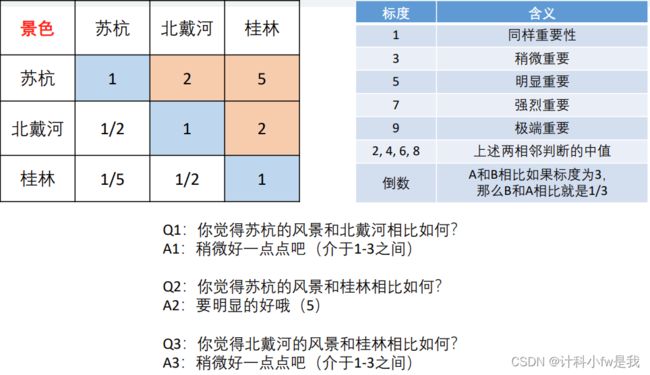
如果用1-9表示重要程度，请你两两比较上述这五个指标对于选择最终的旅游景点的重要性。
就这样，小明回答了C(5,2)次，填好了上面这张表，实际情况下没有小明帮我们回答，具体我们等后面再说。
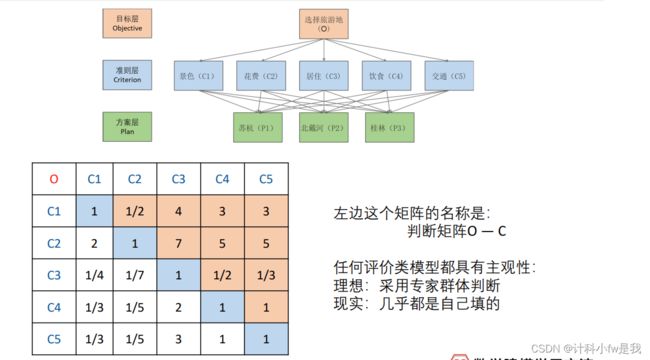
上面这个表是一个5x5的方阵，我们记为A，对应的元素为aij。
(1)aij表示的意思是，与指标j相比，i的重要程度
(2)当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1
(3)aij>0且满足aijxaji=1，我们称满足这一条件的矩阵为正互反矩阵
实际上，上面这个矩阵就是层次分析法中的判断矩阵，得到了判断矩阵，就可以计算出权重了，稍后再进行介绍
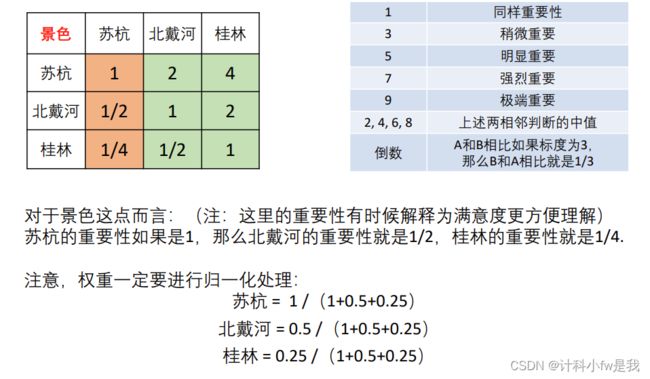
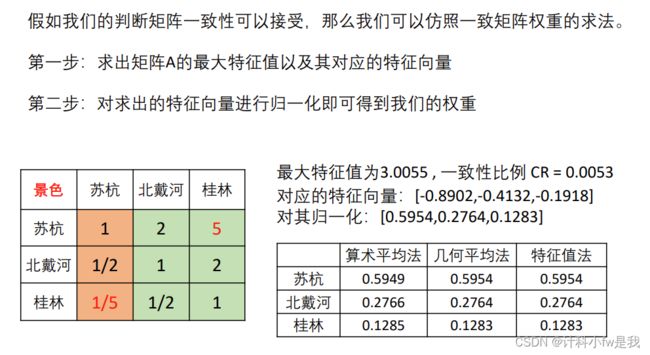
那如何计算苏杭、北戴河与桂林在景色方面的权重(得分)呢？
首先填写判断矩阵
但有一个可能出问题的地方： 
一致矩阵
若矩阵中每个元素ij>0且满足ijxaji=1 ，则我们称该矩阵为正互反矩阵。
在层次分析法中，我们构造的判断矩阵均是正互反矩阵。
若正互反矩阵满足aijxajk=aik，则我们称其为一致矩阵。注意：在使用判断矩阵求权重之前，必须对其进行一致性检验
一致性检验
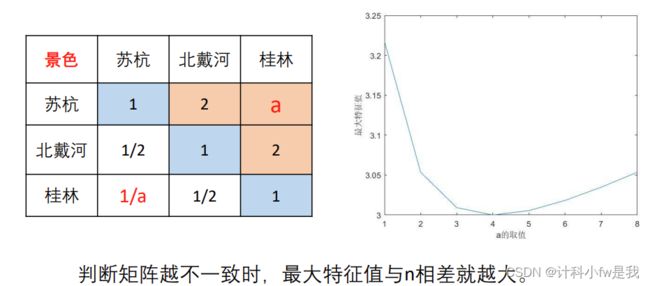
原理：检验我们构造的判断矩阵和一致矩阵是否有太大的差别
因为还没学线代，所以证明过程就略过去了
若正互反矩阵(判断矩阵)满足aijxajk=aik，则我们称其为一致矩阵
一致性检验的步骤
至于平均一致性指标RI是怎么计算来的？
计算一致矩阵的权重
先从简单的开始
我们发现是不一样的，所以我们要求出平均值
方法一：算术平均法求权重
方法二：几何平均法求权重
方法三：特征值法求权重
权重填入表中：
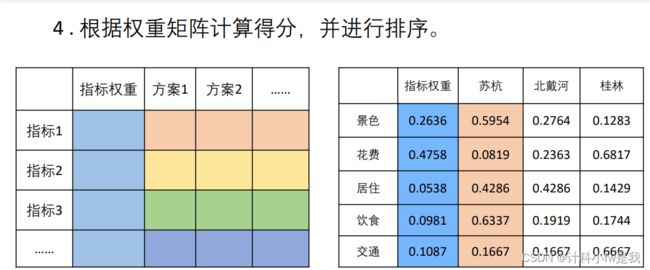
算出得分：
类似的，我们可以得到另外两个的得分，这里可以用EXCEL计算减轻工作量，要点是要用F4锁定单元格
层次分析法(AHP)的主要特点是通过建立递阶层次结构，把人类的判断转化到若干因素两两之间重要度的比较上，从而把难于量化的定性判断转化为可操作得到重要度的上面
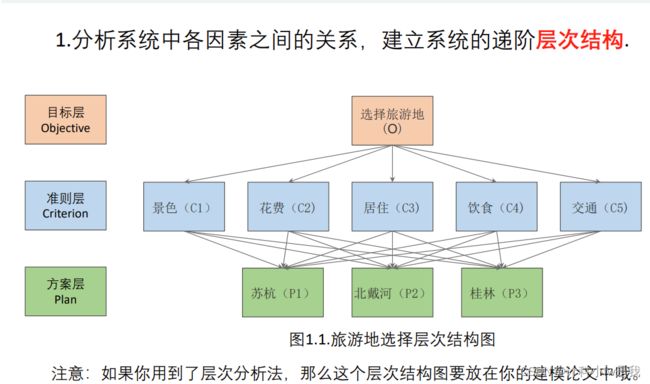
层次分析法的步骤
第一步：
我们可以使用SmartArt生成，也可以使用专业软件：亿图图示
第二步： 
第三步：
如果CR大于0.10，这时候我们需要对矩阵进行调整，往一致矩阵上调整，一致矩阵各行成倍数关系
第四步：
层次分析法也有局限性：
评价的决策层不能太多，否则n会大。判断矩阵和一致矩阵差异可能会很大
还有就是如果决策层指标数据已知，我们怎么来更好的评价呢？
下次进行代码实现！