树状数组及其LeetCode应用详解

本博文所有的代码均可在
https://github.com/Hongze-Wang
中找到，欢迎star。

树状数组又称二叉索引树(Binary Indexed Tree)，以其发明者又命名为Fenwick树，最早由Peter.M.Fenwick以A New Data Structure for Cumulative Frequence Tables作为论文题目发表在期刊Software Practice and Experience(目前SCI 三区)。如题，是用来计算数据压缩时的累计频率(cumulative frequency)的计算问题，现在常用于高效计算数列的前缀和，区间和。-百度百科。

树状数组

树状数组即二叉索引树，是使用数组模拟树形结构的一种数据结构，可用于计算前缀和和区间和(元素全为1时可用来计数)。采用数组而不是直接建树来解决问题是由于某些特定问题比如区间求和完全可以不建树就能解决，这样实现简单，复杂度低。这点上和Trie树有异曲同工之妙。

树状数组可以解决区间上的求和以及更新问题，应用广泛。

凡是树状数组能解决的问题，用线段树也能够解决，但树状数组的系数要少很多，因此实现比较简单。当然一些复杂区间问题还是得用线段树，树状数组功能有限。

时间复杂度上，修改和查询都是O(logn)，比传统数组在求和时要快很多，而且容易实现。

树状数组(二叉索引树)

二叉树的结构可以使用下图来表示，相较于传统的树型图，这里为了说明做了对齐。

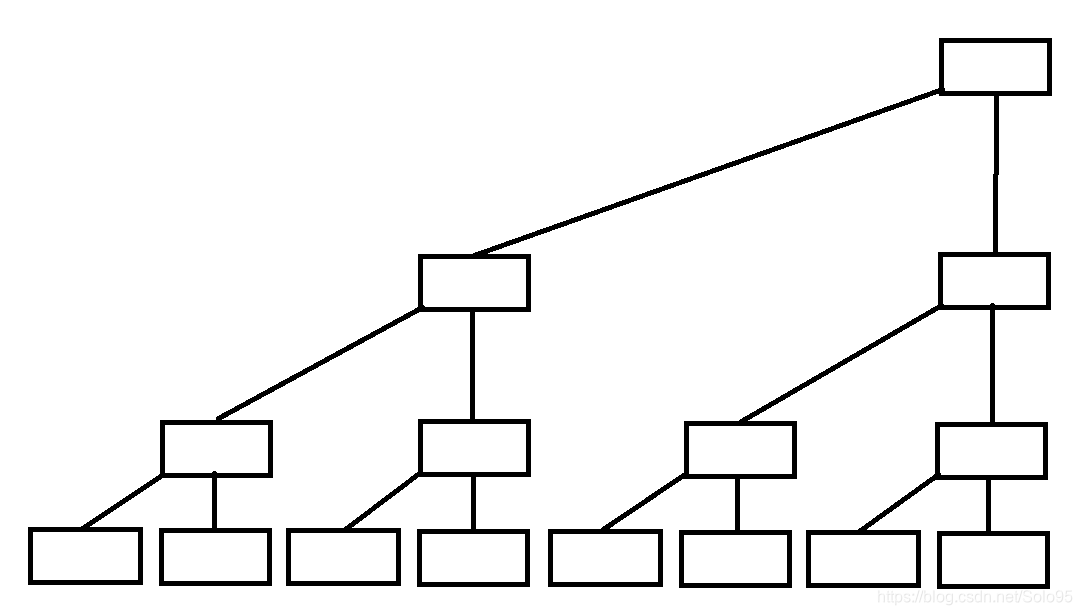
假设叶子结点全部来自一个数组，如果在所有父亲结点存储其直接后代节点的和，那么所有的父亲结点都存储了数组某个区间和，根节点储存了整个数组的和。

理论上如上所述。实际实现时，为了能用数组存储并且实现额外的功能，采用如下的形式来存储：

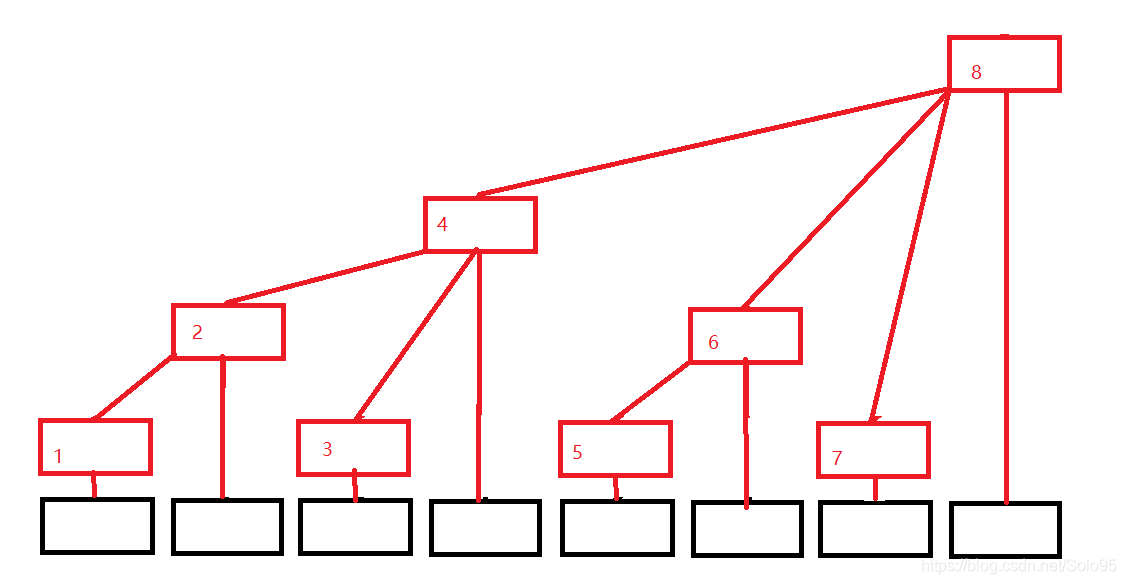
即多叉树，一部分节点存数组的一个元素值，另一部分数组存区间和。

叶子节点(黑色)代表原始数组A，非叶节点(红色)代表树状数组B，那么B可以由A的值按如下方式进行构造。

B[1] = A[1]
B[2] = A[1] + A[2]
B[3] = A[3]
B[4] = A[1] + A[2] + A[3] + A[4]
B[5] = A[5]
B[6] = A[5] + A[6]
B[7] = A[7]
B[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]

如果索引从1开始，那么奇数位置存数组原值，偶数位置存区间和。可以类推，如果索引从0开始，那么偶数位置存数组原值，奇数位置存区间和。实际实现都是从1开始，舍弃掉0的空间，我觉得可能是为了和树的概念对齐，因为树的根节点为1号节点。这篇博文默认索引从1开始。

可以归纳出如下规律：
$B[i]=A[i-2^k+1]+A[i-2^k+2]+...+A[i]$
编程可用循环实现。

其中k表示从i的二进制表示下最低位到最高位连续0的长度(或者说1左移k位等于i)，如果i为奇数(即最低位直接就是1了)，则为0，此时$B[i]=A[i]$。

区间求和如何实现：
$SU{M}_i=B[i]+B[i-2^{k_1}]+B[(i-2^{k_1})-2^{k_2}]+...$
编程可以使用循环实现。

循环一个必要步骤是计算$2^k$，不难得到$2^k=i\&(i\oplus (i-1))$，i异或i-1从得到低位开始的第一个1之间全为0的mask，与运算直接得到了2右移k位的结果。

而$i\oplus (i-1)=-i$，因为负数采用补码存储，等价于原码取反后加1，等价于i和i-1异或。

那么$2^k=i\&(-i)$，这个运算有专门的称呼lowbit。

树状数组建立模板C++代码

int n;
int b[1005];

int lowbit(int x) {
	return x&(-x);
}

void update(int i, int k) {
	while(i < n) {
	    b[i] += k;
	    i += lowbit(i);
	}
}

int getSum(int i) {
	int res = 0;
	while(i > 0) {
		res += b[i];
		i -= lowbit(i);
	}
	return res
}

例题：面试题 10.10. Rank from Stream LCCI

class StreamRank {
private:
    const static int SIZE = 5e4+10;
    int tree[SIZE];

    int lowbit(int x) {
        return x&(-x);
    }
public:
    StreamRank() {
        memset(tree, 0, sizeof(tree));
    }
    
    void track(int x) {
        for(int i=x+1; i<SIZE; i += lowbit(i)) {
            tree[i] += 1;
        }
    }
    
    int getRankOfNumber(int x) {
        int res = 0;
        for(int i=x+1; i>0; i -= lowbit(i)) {
            res += tree[i];
        }
        return res;
    }
};

/**
 * Your StreamRank object will be instantiated and called as such:
 * StreamRank* obj = new StreamRank();
 * obj->track(x);
 * int param_2 = obj->getRankOfNumber(x);
 */

参考

树状数组详解