matlab学习笔记（七）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、 LTI系统的响应

matlab中有专门用于求解连续系统冲激响应和阶跃响应， 并绘制其时域波形的函数impulse( ) 和step( )。如果系统输入为f(t)，冲激响应为h(t)，系统的零状态响应为y(t)，则有：y(t)=h(t)*f(t) 。
lsim( )函数很容易就能对上述微分方程所描述的系统的响应进行仿真，求出系统在任意激励信号作用下的响应。lsim( )函数不仅能够求出连续系统在指定的任意时间范围内系统响应的数值解，而且还能同时绘制出系统响应的时域波形图。

impulse( ) 函数

impulse( )将绘制出由向量a和b所表示的连续系统在指定时间范围内的单位冲激响应h(t)的时域波形图，并能求出指定时间范围内冲激响应的数值解。

impulse(b,a)    			@绘出由向量a和b所定义的连续系统的冲激响应的时域波形。
impulse(b,a ,t0)        	@ 绘出由向量a和b所定义的连续系统在0 ~ t0时间范围内冲激响应的时域波形。
impulse(b,a,t1:p:t2)      	@绘出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的时域波形。
y=impulse(b,a,t1:p:t2);   	@求出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的数值解，但不绘出其相应波形。

step( )函数

step( b,a)					@绘出由向量a和b所定义的连续系统的冲激响应的时域波形。
step(b,a,t0)				@ 绘出由向量a和b所定义的连续系统在0 ~ t0时间范围内冲激响应的时域波形。
step(b,a,t1:p:t2)			@绘出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的时域波形。
y=step(b,a,t1:p:t2) 		@求出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的数值解，但不绘出其相应波形。

lsim( )函数

据系统有无初始状态，lsim( )函数分为以下两种调用格式：

系统无初态时

lsim(b,a,x,t)  @绘出由向量a和b所定义的连续系统在输入为x和t所定义的信号
y=lsim(b,a,x,t) @不绘制出系统的零状态响应曲线，而只是求出与向量t定义的时间范围相一致的系统零状态响应的数值解。

系统有初始状态时

lsim(A,B,C,D,e,t,X0)	@绘出由系数矩阵A,B,C,D所定义的连续时间系统在输入为e和t所定义的信号
[Y,X]= lsim(A,B,C,D,e,t,X0) 	@不绘出全响应波形，而只是求出与向量t定义的时间范围相一致的系统输出向量Y的全响应以及状态变量X的数值解。

二、使用步骤

案例一：若某连续系统的输入为f(t)，输出为y(t)，系统的微分方程为：
q1.求该系统的单位冲激响应h(t)及其单位阶跃响应g(t)。
q2.若f(t)=e^-2t ε (t) ，求出系统的零状态响应y(t)
a1.

a=[1  5  6];b=[3  2];
subplot(2,1,1), impulse(b,a,4)
subplot(2,1,2), step(b,a,4)

输出结果：

q2.

a=[1  5  6];b=[3  2];
p1=0.01;              %定义取样时间间隔为0.01
t1=0:p1:4;            %定义时间范围
x1=exp(-2*t1);       %定义输入信号
lsim(b,a,x1,t1),       %对取样间隔为0.01时系统响应进行仿真
hold on;               %保持图形窗口以便能在同一窗口中绘制多条曲线
p2=0.5;               %定义取样间隔为0.5
t2=0:p2:4;            %定义时间范围
x2=exp(-2*t2);       %定义输入信号
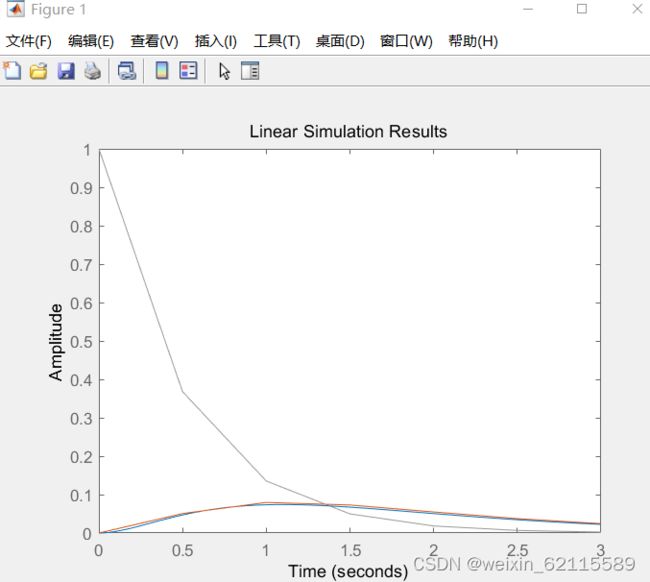
lsim(b,a,x2,t2), hold off   %对取样间隔为0.5时系统响应进行仿真并解除保持

运行结果：

题目：已知描述系统的微分方程和激励信号f(t) 分别如下，试用解析方法求系统的单位冲激响应h(t)和零状态响应r(t)绘制波形。

A1：

a=[1  4  4];b=[1  3];
subplot(2,1,1),impulse(b,a,4)
subplot(2,1,2),step(b,a,4)

a=[1  4  4];b=[1  3];
t1=0:0.01:5;
ut=stepfun(t1,0);
x1=exp(-t1).*ut;
lsim(b,a,x1,t1),
hold on;
t2=0:0.5:5;
ut=stepfun(t2,0);
x2=exp(-t2).*ut;
lsim(b,a,x2,t2),
hold off;

运行结果：

A2：

a=[1  2  26];b=[0 1 0];
subplot(2,1,1),impulse(b,a,5)
subplot(2,1,2),step(b,a,5)

运行结果：

a=[1  2  26];b=[0 1 0];
t1=0:0.01:3;
ut=stepfun(t1,0);
x1=ut;
lsim(b,a,x1,t1),
hold on;
t2=0:0.5:3;
ut=stepfun(t2,0);
x2=ut;
lsim(b,a,x2,t2),
hold off;

运行结果：

A3

a=[1  4  3];b=1;
subplot(2,1,1),impulse(b,a,5)
subplot(2,1,2),step(b,a,5)

a=[1  4  3];b=1;
t1=0:0.01:3;
ut=stepfun(t1,0);
x1=exp(-2*t1).*ut;
lsim(b,a,x1,t1),
hold on;
t2=0:0.5:3;
ut=stepfun(t2,0);
x2=exp(-2*t2).*ut;
lsim(b,a,x2,t2),
hold off;