物理光学-4.光的偏振
物理光学-4.光的偏振
- 1.自然光和偏振光
-
- 1.1自然光
- 1.2偏振光
- 1.3偏振光的合成与分解
- 2.偏振光的起偏与检偏
-
- 2.1偏振片的起偏
- 2.2偏振片的检偏
- 2.3马吕斯定律
- 3.反射和折射时光的偏振
-
- 3.1反射和折射时光的偏振态的变换
- 3.2布儒斯特定律
- 4.双折射起偏振法
-
- 4.1晶体的双折射现象
- 4.2寻常光与非常光
- 4.3双折射现象的理论解释
- 4.4波片
1.自然光和偏振光
1.1自然光
无限多个振幅相等、振动方向任意、彼此之间没有固定相位关系的光振动的组合,叫做自然光。
1.2偏振光
偏振是对横波而言的,光矢量E偏向于某些方向,相对于传播方向成非轴对称分布的光称为偏振光。
-
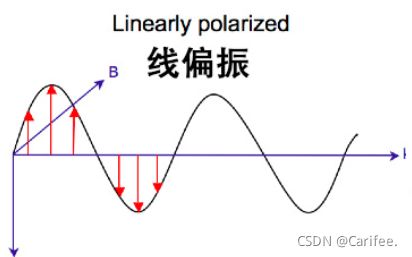
线偏振光
在垂直于传播方向的平面内,光矢量E的振动只限于某一固定方向的光成为线偏振光。光振动方向与传播方向所确定的平面叫做振动面。线偏振光沿传播方向各处的光振动始终处于振动面内,所以线偏振光又叫做平面偏振光。
-
部分偏振光
线偏振光与自然光混合后,成为一种全新的偏振状态,这种光虽然具有各个方向的光振动,当时各个方向上的光振动的振幅并不相等,这种光叫做部分偏振光。在晴朗的日子里,蔚蓝色天空所散射的日光多半是部分偏振光。 -
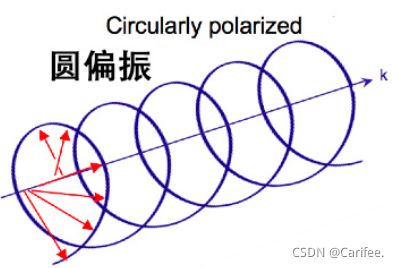
椭圆偏振光和圆偏振光
光矢量E在沿光的传播方向前进的同时,还绕着传播方向以一定的角速度旋转。如果光矢量E的大小不断改变,使其矢端的轨迹在垂直于传播方向的平面内的投影是一个椭圆,这样的偏振光就叫做椭圆偏振光;如果绕传播方向旋转的光矢量E的大小保持不变,则其矢端的轨迹在垂直于传播方向的平面内的投影是一个圆,这样的偏振光则被称为圆偏振光,其时空结构与椭圆偏振光的时空结构类似。根据光矢量E旋转方向的不同,椭圆偏振光和圆偏振光又有左旋光和右旋光之分。
1.3偏振光的合成与分解
根据振动的合成与分解规律,任何一个线偏振光都可以分解为两个同相或反相的垂直线偏振光,反过来,这两个垂直的线偏振光也可以合成一个线偏振光。
自然光可以分解为两个垂直、等幅、无固定相位的线偏振光,每个线偏振光的强度为自然光强度的一半。但是由于这两个垂直的线偏振光之间无固定的相位关系,由同频率的垂直振动的合成规律可知,他们不可能合成为一个线偏振光。
部分偏振光可以分解为两个垂直、不等幅、无固定相位关系的线偏振光,这两个垂直的线偏振光也不能合称为一个线偏振光。
光的偏振状态可以用图示表示,箭头表示光的传播方向,短线表示平行于纸面的光振动,点表示垂直于纸面的光振动。

2.偏振光的起偏与检偏
将自然光变成偏振光的过程成为起偏,所用的光学器件成为起偏器;检验某束光是否是偏振光的过程叫做检偏所用的光学器件叫做检偏器。
2.1偏振片的起偏
某些晶体对不同方向的光振动具有选择吸收的特性,它能吸收某一方向的光振动,而只让与这一方向垂直的光振动通过,晶体的这种特性叫做二向色性,例如,天然的电气石晶体以及液晶就具有二向色性。但是因为天然晶体尺寸小,成本高,所以更常用的是人工的偏振片(polaroid)。
2.2偏振片的检偏
偏振片既可以当起偏器,也可以当检偏器。
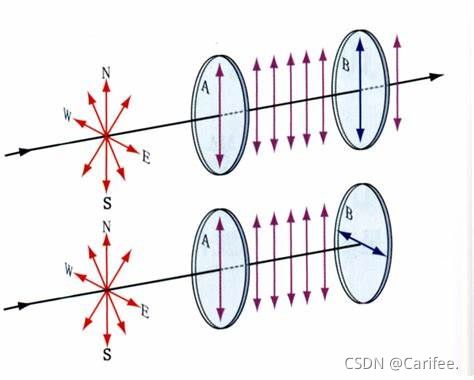
一片偏振片即可以充当检偏器,线偏振光:旋转偏振片,光强会从极大到极小,再从极小到极大,两次最强,两次消光;圆偏振光:旋转偏振片,光强恒为入射光强度的一半,看不到明暗强弱的变化。等等。
2.3马吕斯定律
线偏振光透过检偏器以后,光强度会有什么变化?法国工程师马吕斯率先研究了这一内容。
马吕斯定律: 强度为 I 0 I_{0} I0的线偏振光垂直入射到检偏器上,透过线偏振光的强度为: I = I 0 c o s 2 θ I=I_{0}cos^2\theta I=I0cos2θ
式中,θ为透射线偏振光与入射线偏振光的光振动方向之间的夹角。
3.反射和折射时光的偏振
3.1反射和折射时光的偏振态的变换
大量实验事实表明,反射和折射时,不仅光的传播方向会发生改变,光的偏振态也要发生改变。在反射时,垂直于入射面的振动大于平行于入射面的振动,成为部分偏振光;平行于入射面的振动大于垂直于入射面的振动,成为部分偏振光。那么反射光是否有可能变成完全偏振光呢?英国物理学家布儒斯特的研究结果指出,在一定条件下,反射光可以变成线偏振光。
3.2布儒斯特定律
布儒斯特发现,对于给定的两种各向同性介质,反射光的偏振化程度取决于入射角i。
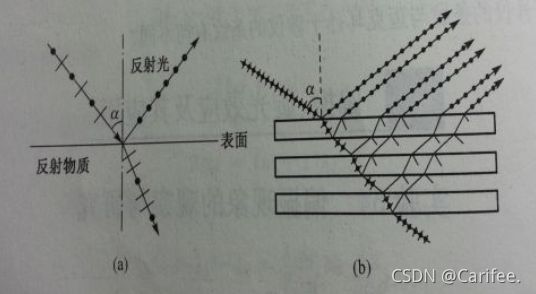 > 当一束光从折射率为 n 1 n_{1} n1的介质射向折射率为 n 2 n_{2} n2的介质时,若入射角i等于某一定值 i b i_{b} ib,则反射光为振动方向垂直于入射面的线偏振光,该定值 i b i_{b} ib满足:
> 当一束光从折射率为 n 1 n_{1} n1的介质射向折射率为 n 2 n_{2} n2的介质时,若入射角i等于某一定值 i b i_{b} ib,则反射光为振动方向垂直于入射面的线偏振光,该定值 i b i_{b} ib满足:
t a n i b = n 2 n 1 tani_{b}={n_{2}\over n_{1}} tanib=n1n2
这就是布儒斯特定律, i b i_{b} ib成为布儒斯特角,也叫起偏角。此时折射角为γ, i b + γ = π 2 i_{b}+\gamma={\pi\over 2} ib+γ=2π
布儒斯特定律具有很多应用价值,比如将光变为完全偏振光,或者用来测量介质的折射率等。
此时,反射光为线偏振光,折射光为部分偏振光,但是,反射光的光强仅为原光强的7%,折射光的光强却占原光强的93%。为了提高反射光的光强和折射光的偏振化程度,可以将很多平行平板堆叠起来,当平行平板的数量非常多时,反射光 的光强就会大大提高,折射光也会变成完全偏振光。如上图中(b)所示。
4.双折射起偏振法
4.1晶体的双折射现象
我们知道,介质可以分为各向同性介质和各向异性介质,其中各向异性介质的折射率n因光的传播方向和光矢量的振动方向不同而具有不同数值,各向同性介质的折射率n则对各个方向都是相同的。
正常情况下,折射现象的第二种介质为各向同性介质时,折射光线只有一条;但是当第二种介质为各向异性介质时,折射光线会分为两条,这种现象就叫做**双折射现象。**常见的双折射现象有方解石晶体的双折射现象,比如你把方解石晶体放在一张写有字的纸面上时,将会看到每个字都成双像。
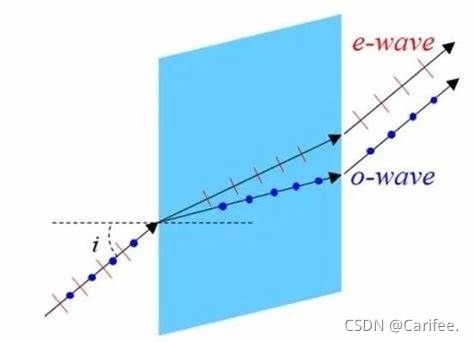
4.2寻常光与非常光
- 寻常光与非常光
双折射现象的两条折射光中,有一条服从折射定律(折射角为 γ o \gamma_{o} γo),称为寻常光(o光),折射率 n o n_{o} no是一个确定的常数,与入射角i的变化无关。
n 0 = s i n i s i n γ o n_{0}={sini\over{sin\gamma_{o}}} n0=sinγosini
而另一条不符合折射定律的折射光叫做非常光,简称e光。
n e ( i ) = s i n i s i n γ e n_{e}(i)={sini\over{sin\gamma_{e}}} ne(i)=sinγesini - 光轴
晶体中不发生折射现象的特殊方向成为光轴,天然方解石晶体是每个表面都是锐角为78°、钝角为102°的平行六面体,有八个顶角,其中一个顶角为三个钝角102°的交点,称为钝隅。 过钝隅且与钝隅的三条棱边成等角的直线方向,即为方解石晶体的光轴,当方解石晶体的各棱长度相等时,两个相对钝隅的连线即为光轴。
应该指出的是,光轴并不限于某一特殊的直线,而是代表晶体内某一特定的方向,过晶体内任意点所做的平行于此方向的直线都是晶体的光轴。
只有一个光轴方向的晶体叫做单轴晶体,如方解石、石英、红宝石等;而有两个光轴方向的晶体叫做双轴晶体,例如云母、硫磺、蓝宝石。
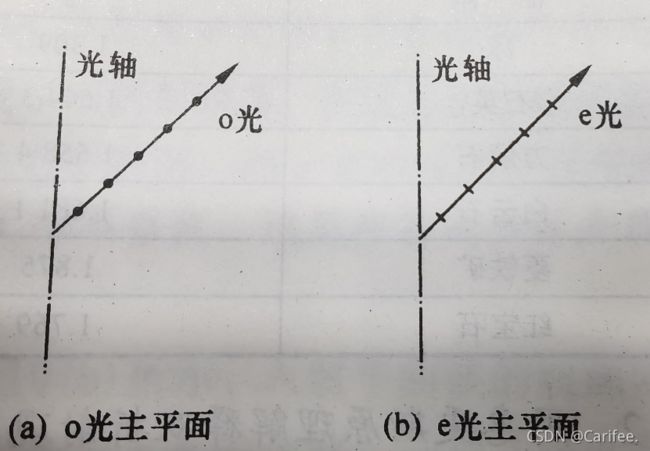
在晶体中,某条光线与晶体光轴所构成的平面叫做该光线的主平面。o光和e光各有一个主平面,分别叫做o光主平面和e光主平面。
- o光和e光的偏振态
实验表明,o光和e光都是线偏振光,o光光矢量的振动方向垂直于o光主平面,而e光光矢量的振动方向就在e光主平面内。由于o光恒在入射面内,而e光一般不在入射面内,所以o光主平面与e光主平面一般并不重合,二者之间存在一微小夹角。这就是说,一般情况下,o光和e光光矢量的振动方向近似垂直。在特殊情况下,即当光轴在入射面内时,o光和e光的主平面都与入射面重合。在这种情况下,o光和e光光矢量的振动方向严格垂直。
4.3双折射现象的理论解释
仅用惠更斯原理对光的双折射现象进行定性的说明。理论表明,o光在晶体中沿各个方向的传播方向都相同,所以在晶体中o光波面上任一点P所发出的子波波面为球面;而e光沿不同方向的传播速率不相同,故e光波面上任一点P在晶体中所发出的子波波面是以晶体光轴为轴线的旋转椭球面,如下图所示,沿光轴方向,o光和e光的传播速率相同,两波面在此相切;在垂直于光轴方向上,o光和e光的速率之差最大。用 v o v_{o} vo表示o光在晶体中传播的速率, v e v_{e} ve表示e光在晶体中传播的速率。有一类晶体, v o > v e v_{o}>v_{e} vo>ve,称为正晶体;另一类晶体, v e > v o v_{e}>v_{o} ve>vo,称为负晶体。
4.4波片
光轴平行于表面的晶体薄片叫做波片,铂片通常是用方解石或石英等单轴晶体按需要的厚度切割而成的。
当平行光垂直入射到波片上时,波片中o光和e光均沿原方向传播,但二者的传播速度不同( v o ≠ v e v_{o}\not=v_{e} vo=ve),所以在经过厚度为d的波片后,o光和e光之间就产生了一定的光程差,这一光程差为
δ = ( n o − n e ) d \delta = (n_{o}-n_{e})d δ=(no−ne)d
与之相应的相位差为:
Δ Ψ = 2 π λ ( n o − n e ) d \Delta\Psi ={2\pi\over\lambda} (n_{o}-n_{e})d ΔΨ=λ2π(no−ne)d
由此可见,只要控制波片厚度d,就可以使o光和e光之间产生所期望的光程差(或相位差)。根据光程差的不同,常见的波片又可以分为四分之一波片、半波片、全波片等。
之后便可以使用一个偏振片和一个波片产生椭圆偏振光和圆偏振光。
