备战秋招-数据结构
序言
逐渐进入五月份,距离秋招估计也还有4个月左右。我的目标是前端工程师,虽然可以用Vue做一些东西,但是基础还是不牢固。在看了多篇面经后,大致确定如何补齐自己的短板。
学习方法
1.了解理论
2.实现(Java)
思维导图(来源于知乎)
目录
- 序言
- 学习方法
-
- 1.了解理论
- 2.实现(Java)
- 思维导图(来源于知乎)
- 一、线性表
-
- (一) 链表
-
- 1.单链表
- 2.经典问题-链表双指针
- 3.双链表
- 4.总结
- 5.练习题(LeetCode)
- (二) 栈和队列
-
- 0.前置知识
- 1.队列的实现
- 3.循环队列
- 4.广度优先搜索
- 5.栈的实现
- 6.深度优先搜索DFS
- 二、树
-
- (一) 二叉树
-
- 1.二叉树的基本结构
- 2.实现
- 3.遍历树结构
-
- ①前序遍历
- ②中序遍历
- ③后序遍历
- 三、LeetCode-HOT100刷题
-
- 1.多数元素
- 2.合并二叉树
- 3.翻转二叉树
- 4.二叉树的最大深度
- 5.反转链表
- 6.只出现一次的数字
- 7.合并两个有序链表
一、线性表
(一) 链表
参考资料
1.单链表
单链表的构成很简单,就是一个值,一个指向下一个节点的指针。

它的缺点也很明确,就是查找任意一个节点都要从头开始,那么这是非常令人不能接受的。不过它也有优点,也就是增删改查比较简单。
代码部分也很简单,以下为代码(基本实现,不含异常处理):
package singlyList;
import java.security.PublicKey;
class ListNode{
int val; //每个节点都有一个值。
ListNode next; //每一个节点都指向下一个节点
ListNode(int x){
this.val = x;
}
}
class mylist{
ListNode head; //定义头节点
int length; //定义链表长度
public void init(int x) { //初始化头节点
head=new ListNode(x);
length=1;
}
public void addNode(int x) { //增加操作
ListNode Node = null; //记录节点
if(length == 1) { //链表长度为1,即只有头节点。
ListNode a =new ListNode(x);
head.next = a;
length++;
}
else {
Node = head;
for(int i=0;i<length;i++) { //找到末尾节点
if(Node.next!=null) {
Node=Node.next; //找到没有后继节点的节点
}
else {
break;
}
}
Node.next = new ListNode(x); //给最后一个节点添加后继
length++;
}
}
public void insertNode(int x,int index) { //插入操作
ListNode nod = head; //头节点标记
ListNode a = null; //前节点记录
ListNode in = new ListNode(x); //插入节点初始化
for(int i=1;i<index;i++) { //找到前置节点
if(i == index-1) { //记录前置节点
a = nod.next;
}
nod=nod.next;
}
in.next = nod.next; //当前节点后继节点为前置节点的后继节点
a.next=in; //前置节点的后继为插入的节点
}
public int retrieve(int index) { //检索操作
ListNode a = head;
if(length<index) { //如果索引超出长度,返回-1
return -1;
}
else {
for(int i=0;i<index;i++) { //找到索引对应位置的节点
a = a.next;
}
return a.val;
}
}
public void del(int index) { //删除操作
ListNode a = head; //记录头节点
ListNode b = null; //记录目标前节点
for(int i=0;i<index;i++) {
if(i==index-1) {
b=a; //记录前节点
}
a = a.next;
}
if(a.next != null) {//如果目标节点有后继节点,则将目标前节点的next指向目标的后节点
b.next=a.next;
}
b.next=null;
}
}
2.经典问题-链表双指针
在链表中分为,循环链表和非循环链表,如何区分他们呢即可以采用两种方法,最原生的就是双指针,设计一个快指针,一个慢指针,类似龟兔赛跑,它们如果在一个循环中跑,快指针终究会追到慢指针,由此我们可以判断链表是否是循环链表。
代码:
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
if(head != null){
ListNode nod = head;
ListNode Snod = head;
int count=0;
while(nod.next!=null){
if(count%2==0 || count == 0){
nod = nod.next;
count++;
}
else{
nod = nod.next;
Snod = Snod.next;
count++;
}
if(nod == Snod){
return true;
}
}
}
return false;
}
}
对于该类问题Leetcode给出了一个模板:
// Initialize slow & fast pointers
ListNode slow = head;
ListNode fast = head;
/**
* Change this condition to fit specific problem.
* Attention: remember to avoid null-pointer error
**/
while (slow != null && fast != null && fast.next != null) {
slow = slow.next; // move slow pointer one step each time
fast = fast.next.next; // move fast pointer two steps each time
if (slow == fast) { // change this condition to fit specific problem
return true;
}
}
return false; // change return value to fit specific problem
3.双链表
双链表除了有后继还要指明前驱。

实际的实现并不难.
节点结构如下:
class ListNode{
int val;
ListNode pre;//前驱
ListNode next;//后继
ListNode(int x){
this.val = x;
}
}
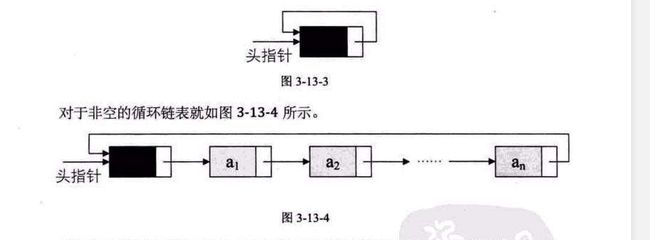
在双链表中,我们如果将最后一个节点的后继设为头节点,将头节点的前驱设为最后一个节点。
我们就会得到一个循环链表。
4.总结
单链表和双链表的表现在许多操作中是相似的。
它们都无法在常量时间内随机访问数据。
它们都能够在 O(1) 时间内在给定结点之后或列表开头添加一个新结点。
它们都能够在 O(1) 时间内删除第一个结点。
但是删除给定结点(包括最后一个结点)时略有不同。
1.在单链表中,它无法获取给定结点的前一个结点,因此在删除给定结点之前我们必须花费 O(N) 时间来找出前一结点。
2.在双链表中,这会更容易,因为我们可以使用“prev”引用字段获取前一个结点。因此我们可以在 O(1) 时间内删除给定结点。
5.练习题(LeetCode)
参考资料以及习题
(二) 栈和队列
在这一段将学习如何实现栈和队列。
之所以放在一起是因为他们是很相似的。
队列是先入先出
栈是先入后出
在此,应用LeetCode的动态图进行解释
队列:
栈:
0.前置知识
在正式开始实现前,我们需要知道Java中如何实现动态数组。
Java.util.ArrayList类是一个动态数组类型,ArrayList对象既有数组的特征,也有链表的特征。可以随时从链表中添加或删除一个元素。ArrayList实现了List接口。
///定义一个动态数组
ArrayList<Integer> a = new ArrayList<Integer>();
1.队列的实现
class MyQueue {
// 存储元素
private List<Integer> data;
// 指示起始位置的指针
private int p_start;
public MyQueue() {
data = new ArrayList<Integer>();
p_start = 0;
}
/** 在队列中插入元素。如果操作成功,则返回true。 */
public boolean enQueue(int x) {
data.add(x);
return true;
};
/** 从队列中删除元素。如果操作成功,则返回true。 */
public boolean deQueue() {
if (isEmpty() == true) {
return false;
}
p_start++;
return true;
}
/** 从队列中获取前面的项。 */
public int Front() {
return data.get(p_start);
}
/** 检查队列是否为空。 */
public boolean isEmpty() {
return p_start >= data.size();
}
};
这是最简单的实现,但是弊端很明显,就是我们的队列只能无限增长,如果之前的值弹出后,会留下空的空间,这导致空间被浪费了,所以我们引入了循环队列。
3.循环队列
具体来说,我们可以使用固定大小的数组和两个指针来指示起始位置和结束位置。
class MyCircularQueue {
private int[] data;
private int head;
private int tail;
private int size;
/** 在此处初始化数据结构。将队列的大小设置为k。 */
public MyCircularQueue(int k) {
data = new int[k];
head = -1;
tail = -1;
size = k;
}
/** 在循环队列中插入元素。如果操作成功,则返回true。 */
public boolean enQueue(int value) {
if (isFull() == true) {
return false;
}
if (isEmpty() == true) {
head = 0;
}
tail = (tail + 1) % size;
data[tail] = value;
return true;
}
/** 从循环队列中删除元素。如果操作成功,则返回true */
public boolean deQueue() {
if (isEmpty() == true) {
return false;
}
if (head == tail) {
head = -1;
tail = -1;
return true;
}
head = (head + 1) % size;
return true;
}
/** 从队列中获取前面的项 */
public int Front() {
if (isEmpty() == true) {
return -1;
}
return data[head];
}
/** 从队列中获取最后一项 */
public int Rear() {
if (isEmpty() == true) {
return -1;
}
return data[tail];
}
/** 检查循环队列是否为空 */
public boolean isEmpty() {
return head == -1;
}
/** 检查循环队列是否已满 */
public boolean isFull() {
return ((tail + 1) % size) == head;
}
}
4.广度优先搜索
广度优先搜索(BFS)的一个常见应用是找出从根结点到目标结点的最短路径。
理解:
模板:
/**
* 返回根节点和目标节点之间最短路径的长度
*/
int BFS(Node root, Node target) {
Queue<Node> queue; // 存储等待处理的所有节点
Set<Node> used; // 存储所有使用的节点
int step = 0; // 从根节点到当前节点所需的步骤数
// 初始化
add root to queue;
add root to used;
// BFS
while (queue is not empty) {
step = step + 1;
// 迭代已经在队列中的节点
int size = queue.size();
for (int i = 0; i < size; ++i) {
Node cur = the first node in queue;
return step if cur is target;
for (Node next : the neighbors of cur) {
if (next is not in used) {
add next to queue;
add next to used;
}
}
remove the first node from queue;
}
}
return -1; // 从根到目标没有路径
}
5.栈的实现
// "static void main" must be defined in a public class.
public class Main {
public static void main(String[] args) {
// 1. Initialize a stack.
Stack<Integer> s = new Stack<>();
// 2. Push new element.
s.push(5);
s.push(13);
s.push(8);
s.push(6);
// 3. Check if stack is empty.
if (s.empty() == true) {
System.out.println("Stack is empty!");
return;
}
// 4. Pop an element.
s.pop();
// 5. Get the top element.
System.out.println("The top element is: " + s.peek());
// 6. Get the size of the stack.
System.out.println("The size is: " + s.size());
}
}
6.深度优先搜索DFS
/*
* Return true if there is a path from cur to target.
*/
boolean DFS(Node cur, Node target, Set<Node> visited) {
return true if cur is target;
for (next : each neighbor of cur) {
if (next is not in visited) {
add next to visted;
return true if DFS(next, target, visited) == true;
}
}
return false;
}
二、树
(一) 二叉树
1.二叉树的基本结构
二叉树是一种更为典型的树状结构。如它名字所描述的那样,二叉树是每个节点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
在添加子树时往往需要通过数值大小来添加,即:
比上级树节点值小的,放到左子树
比上级树节点值大的,放到右子树
2.实现
在实现这一部分中,你需要知道如何创建一个栈。
节点代码如下:
class treenode{
int val;
treenode left;
treenode right;
treenode(){}
treenode(int x){
this.val=x;
this.left=null;
this.right=null;
}
treenode(int x,treenode left,treenode right){
this.left=left;
this.val=x;
this.right=right;
}
}
树代码如下:
public class BinaryTree {
treenode root;
public void init(int x) {
root = new treenode(x);
}
public void insertnode(int x) {
treenode nod=root;
Stack<treenode> stack = new Stack<>();
while(nod!=null) {
stack.push(nod);
if(x<=nod.val) {
nod = nod.left;
}
else if(x>nod.val) {
nod = nod.right;
}
}
if(!stack.isEmpty()) {
nod= stack.pop();
if(x>nod.val) {
nod.right=new treenode(x);
}
else {
nod.left=new treenode(x);
}
}else {
if(x>root.val) {
root.right=new treenode(x);
}
else {
root.left=new treenode(x);
}
}
}
}
3.遍历树结构
在这一部分中,你要知道树的遍历方法,以及他们的特点。
它们的遍历顺序如下:
前序遍历:根节点-左子树-右子树
中序遍历:左子树-根节点-右子树
后序遍历:右子树-左子树-根节点
通常来说,后序遍历的结果和前序遍历的结果相反。
①前序遍历
public List<Integer> PreorderTraversal(){
treenode nod=root;
List<Integer> a = new ArrayList<>();
Stack<treenode> stack = new Stack<>();
while(nod != null || !stack.isEmpty()) {
while(nod!=null) {
stack.push(nod);
a.add(nod.val);
nod = nod.left;
}
nod = stack.pop().right;
}
return a;
}
②中序遍历
public List<Integer> InorderTraversal(){
List<Integer> a = new ArrayList<>();
Stack<treenode> stack = new Stack<>();
treenode nod = root;
while(nod !=null || !stack.isEmpty()) {
while(nod!=null) {
stack.push(nod);
nod=nod.left;
}
nod = stack.pop();
a.add(nod.val);
nod = nod.right;
}
return a;
}
③后序遍历
public List<Integer> PostorderTraversal(){
List<Integer> a = PreorderTraversal();
Collections.reverse(a);
return a;
}
三、LeetCode-HOT100刷题
https://leetcode-cn.com/problemset/all/?listId=2cktkvj
1.多数元素
题干:
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
解题:
方法一:数组排序,选中位数
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length/2];
}
}
方法二:摩尔投票法(本质相互抵消,相同+1,不同-1,最后留下来的就是众数,或者合格的数)
class Solution {
public int majorityElement(int[] nums) {
int res=0;
int count=0;
for(int i=0;i<nums.length;i++){
if(count==0){
res = nums[i];
count++;
}else{
if(res==nums[i]){count++;}
else{count--;}
}
}
return res;
}
}
2.合并二叉树
解题方法(递归分治):
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1 == null){
return root2;
}
if(root2==null){
return root1;
}
TreeNode root = new TreeNode(root1.val+root2.val); //新的根结点
root.left = mergeTrees(root1.left,root2.left); //左边合并
root.right = mergeTrees(root1.right,root2.right); //右边合并
return root; //返回新节点
}
}
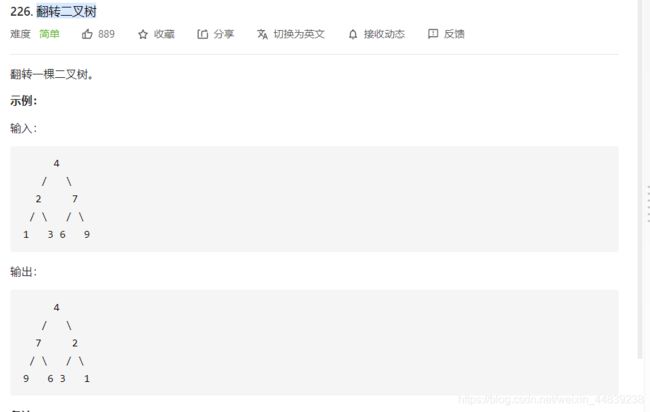
3.翻转二叉树
解题方法:(递归,分治)
分析问题发现细分后,其实也就是取出左节点,取出右节点,然后替换原来的左右节点。
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null){
return null;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right=left;
return root;
}
}
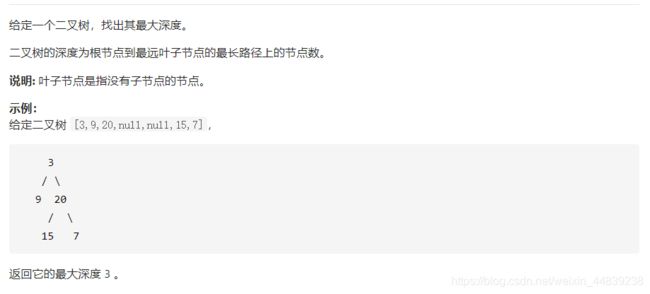
4.二叉树的最大深度
解题方法:(分治,递归)
本题细化后,实质就是比较两边谁的节点多,当找到为null的节点开始返回值0,之后每一次判断左边的值和右边的值谁大,并且给较大值+1,加的是本层的深度。
class Solution {
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
if(left > right){
return left+1;
}else{
return right+1;
}
}
}
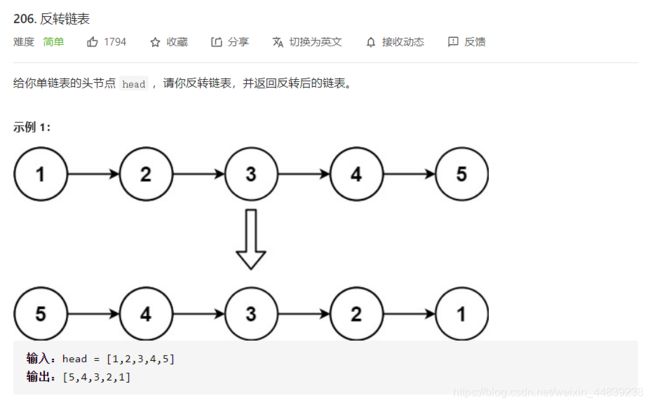
5.反转链表
方法一:(栈解法)
因为本题反转链表实际就是,后入先出的问题。所以我认为栈解法是最好的。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode node = null; //定义指针
Stack<ListNode> sk = new Stack<ListNode>(); //定义栈
while(head!=null){ //将所有节点放入栈
sk.push(head);
head= head.next;
}
head = sk.pop(); //新的头节点是最后一个入栈的节点
head.next = sk.pop(); //头节点下一个指向倒数第二个节点
node = head.next; //指向第二个新节点
while(!sk.isEmpty()){ //如果栈不为空
node.next = sk.pop(); //指向下一个节点
node = node.next; //指针移动
}
node.next = null; //将最后一个节点,即原来的头节点的下一个节点置空
return head;
}
}
方法二:(递归,分治)
通过上面的解法,可以分析出来,本题其实,就是找到新的头节点,然后反转指针的过程,所以递归也是好的解法。
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode newhead = reverseList(head.next); //找到新的头
head.next.next = head; //将当前节点的下一个节点指向自己
head.next = null; //指针置空,防止循环链表
return newhead;
}
}
6.只出现一次的数字
题干
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
输入: [2,2,1]
输出: 1
解题
class Solution {
public int singleNumber(int[] nums) {
int a = 0;
for(int numse:nums){
a = numse^a;
}
return a;
}
}
使用的是异或法。
异或(两个相应bit位相同,则结果为0,否则为1)
也就是用0和元素比较,如果出现第二次则会改变会0,
只有出现过一次的数字会被保留到最后。
7.合并两个有序链表
题干

解题思路:
本题其实可以划分最小问题,使用递归解决。
即判断值,小的值作为当前节点,剩下的值继续递归。
具体代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1==null && l2==null){
return l1;
}else if(l1==null){
return l2;
}else if(l2==null){
return l1;
}
ListNode myroot;
if(l1.val <l2.val){
myroot= l1;
}else{
myroot= l2;
}
if(l1.val <l2.val){
l1.next = mergeTwoLists(l1.next,l2);
}else{
l2.next = mergeTwoLists(l1,l2.next);
}
return myroot;
}
}