论文笔记_Fundamental Performance Limits and Scaling of a CMOS Passive Double-Balanced Mixer

Fundamental Performance Limits and Scaling of a CMOS Passive Double-Balanced Mixer

时间：2008年6月
作者：Krenar Komoni, Sameer Sonkusale, Geoff Dawe

省流

本文仿真了350nm-32nm工艺制程下，FET-Quad无源双平衡混频器的变频增益、1dB压缩点、SSB噪声系数3个参数，并提出FOM参数（类似品质因数，定义见公式12）来综合考量这3个参数。最终得到图5。

研究意义：

1. 工艺制程的缩小会带来FET-Quad混频器性能的提升，但是性能的提升有极限
2. 可以在工程设计过程中，参照图5选择满足自己性能需求的混频器的工艺制程

---

摘要

本文研究了双平衡无源混合器的基本性能和尺寸极限。对无源双平衡混频器的分析将展示晶体管栅长(L_G)的缩小对其性能指标的直接影响。我们根据变频增益(G_C)、1-dB压缩点(P_1-dB)和SSB噪声系数(NF)来分析性能。我们将展示，随着CMOS工艺技术的发展，双平衡无源混频器结构将变得更加有利，并进一步提升性能。我们通过对CMOS从350nm至32nm工艺设计的混频器的仿真和建模结果验证了这一点。我们引入了混频器的品质因数(FOM_MIXER)来比较性能和工艺尺寸。电路设计人员和系统架构师可以使用这篇论文来找到一个满足他们对混频器需求的合适制程。

---

In this paper, fundamental performance limits and scaling of a double-balanced passive mixer are examined. Analysis of the passive double-balanced mixer will show how its performance metrics are directly affected by the down-scaling of the transistor gate length, L_G. We analyze the performance in terms of conversion gain (G_C), 1-dB compression point (P1-dB) which we derive, and SSB Noise Figure (NF). We will show that as CMOS process technology evolves, the double-balanced passive mixer architecture will become more favorable and yield improved performance. This is verified through simulation and modeling results for mixers designed in CMOS 350nm to 32nm technology. We introduce a mixer’s figure-of-merit (FOM_MIXER) to compare performance with technology scaling. Circuit designers and System architects can use this paper to find a suitable process technology that will meet their specifications.

Introduction

FET-Quad 双平衡无源混频器的性能极限在哪里？

1990年早期，双极性晶体管渐渐被性能更好的CMOS管替代，尤其是模拟无线收发机的元件。这带来了一个新问题，CMOS技术可以带我们往前再走多远？

在CMOS技术中，最常用的两种混频器结构是：有源双平衡混频器，或吉尔伯特混频器；无源双平衡混频器，或FET-Quad混频器。
无源混频器的优势有：

• 不需要偏置的直流电流
• 没有静息功耗
• 具有更高的线性度
• 可以在电压域对信号进行整流

无源混频器的缺点：（可以随工艺制程的下降而改善）

• 噪声系数高
• 带宽有限
• 变频损耗大

通过变频增益(G_C)、1-dB压缩点(P_1-dB)和SSB噪声系数(NF)来分析混频器的基本性能极限

虽然没有明说，但是作者的意思应该是：无源混频器优点很突出，劣势能改善，所以无源混频器是趋势。并在后文只介绍了无源双平衡混频器（FET-Quad）

无源双平衡混频器（FET-Quad Mixer）

对无源双混频器（FET-Quad Mixer）进行了简介

无源双平衡混频器，也被称为FET-Quad混频器

• 双平衡结构有助于提高 RF-IF 和 LO-IF 的隔离度
• RF 和 LO 端口通过巴伦产生差分信号（在如图所示的模型中，巴伦认为是理想的）

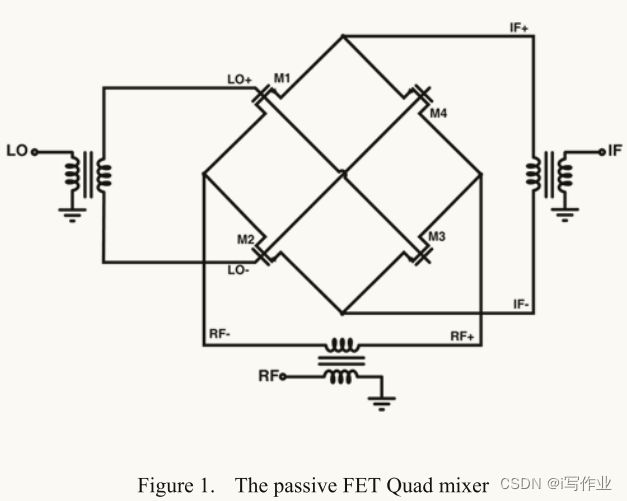
采用CMOS技术的双平衡无源混频器如图1所示：

FET-Quad混频器主要通过4个CMOS管（视作开关）不断的打开关闭来完成。RF信号从漏极输入，IF信号通过源极输出。LO信号从栅极输入，通过调制CMOS管的阻值来在电压域混合RF和LO信号。理想情况下希望LO信号的加入可以在CMOS管栅极的阈值电压附近变化。如图2，采用理想方波进行输入，对应的可以控制CMOS管的导通和关闭（即开关），图2(b)是分析单晶体管混频器的变频损耗模型。

该过程会产生所需的 ${\omega }_{RF}\pm {\omega }_{LO}$ 成分，还有各阶谐波相互混合的杂散 $m{\omega }_{RF}\pm n{\omega }_{LO}$，理想情况下可以通过带通滤波器滤除所有杂散。

对FET-Quad Mixer的分析

分析分为2部分：

1. 介绍单管的非平衡无源混频器，这会帮助分析和建模无源双平衡混频器
2. 对无源双平衡混频器进行分析和建模

对比混频器的如下性能：变频增益、IIP3、1dB压缩点、噪声系数；并在最后引入FOM来综合对比这些性能

由于本文是分析混频器的基本性能极限，所以假设LO信号是理想的方波信号

变频增益

理想的方波信号：
$$v_{LO,square}=\frac{1}{2}+\frac{2}{\pi }\left[sin({\omega }_{LO}t)+\frac{sin(3{\omega }_{LO}t)}{3}+\frac{sin(5{\omega }_{LO}t)}{5}+\cdots \right]\text{\hspace{1em}(1)}$$
假设RF信号为 $cos({\omega }_{RF}t)$，其与理想方波本振相乘（理想单管无源混频）得到的电压最大值为 $1/\pi$，即其理想变频增益为 $20{\log }_{10}(1/\pi )=-9.943dB$。

无源单管混频器最终变频增益的结果由2部分组成：

1. 将混频器视为LTI¹系统，即 not switching
2. 将混频器是为LPTV²系统，即 switching

以下内容参考图2、图3

1.Not Switching - LTI System

为了便于计算，做出如下假设：

• 忽略$R_S,R_D$，因为其远小于$r_{ds}$（on-resistance）

• 假定$Z_{OFF}$的阻抗受线性栅-漏极和栅-源电容的支配

• 在低频低频率情况下，漏极电容和源极电容的非线性可以忽略不计

得到$R_{ON},Z_{OFF}$

$$R_{ON}=r_{ds}=\frac{L_g}{{\mu }_n{C}_{OX}W((V_g-g_c\cdot v_{RF})-V_{th}-V_{ds})}\text{\hspace{1em}(2)}$$

$$Z_{OFF}=\frac{1}{j{\omega }_{RF}(C_{GS(V_{G}S=0)}||C_{GD(VGS=0)})}\text{\hspace{1em}(3)}$$

根据图2(b)，当开关闭合时变频增益为：
$$g_c=\frac{|Z_L|}{|Z_L+R_{ON}||Z_{OFF}|}\text{\hspace{1em}(4)}$$
当开关打开时，变频增益为公式(5)，其变频增益非常接近于0
g c = ∣ Z L Z L + Z O F F ∣ (5) g_c=\left|\frac{Z_L}{Z_L+Z_{OFF}}\right| \tag{5} gc​= ​ZL​+ZOFF​ZL​​ ​(5)
2.Switching - LPTV System

晶体管受理想方波调制不断开关（Switching），其变频增益为：
$$g_c=\frac{1}{\pi }\left(\frac{Z_L}{Z_L+R_{ON}||Z_{OFF}}\right)\text{\hspace{1em}(6)}$$

图1分析的晶体管模型，也适用于FET-Quad的每一个晶体管。将FET-Quad的晶体管替换为图1的模型后，得到图4。在ON-OFF电容均为线性的前提下，得到最终的变频增益方程为(7)
$$G_C=10{\log }_{10}\left(\frac{2}{\pi }\left(\frac{Z_L}{Z_L+R_{ON}||Z_{OFF}}\right)-\frac{2}{\pi }\left(\frac{Z_L}{Z_L+Z_{OFF}}\right)\right)\text{\hspace{1em}(7)}$$
可以看到此模型下FET-Quad的变频增益已经很接近理想值$2/\pi$了

工艺制程的下降会导致 $L_g$、${\mu }_0$、$C_{OX}$、$W$ 发生变化，并带来显著影响：

• $L_g$ 下降，$R_{ON}$ 也会下降，从而改善无源混频器的变频增益
• 通过增加 $W$ 的宽度，也可以减小 $R_{ON}$；但是其固有电容随 $W$ 增加而成比例增加，导致 $Z_{OFF}$ 减小，进而导致混频器工作带宽受限，在[15]³中具体讨论了栅长对截止频率的影响

IF端口的镜频和谐波频率也会对其变频增益带来负面影响，但是本篇文章忽略掉了

1dB压缩点和IIP3

公式(2)表示，$R_{ON}$ 的值与输入电压成比例，（$g_c\cdot v_{RF}$ 越接近 $V_g-V_{th}-V_{ds}$，$R_{ON}$ 越大）；由于 $R_{ON}$ 的非线性性，输出信号 $v_{IF}=g_c\cdot v_{RF}$ 会产生压缩，并最终导致1dB压缩点的出现。

利用多项式拟合该非线性性，得到公式(8)
$$v_{IF}=c_0+c_1{v}_{RF}+c_2{v}_{RF}^2+c_3{v}_{RF}^3+\cdots \text{\hspace{1em}(8)}$$
将 $v_{IF}=g_c\cdot v_{RF}$ 表示为幂级数形式，并求解出了系数后，得到了公式(9)
$$|c_1/c_3|=\frac{Z_L\left(Z_{OFF}-\frac{L_g}{{\mu }_n{C}_{OX}W(V_g-V_{th}-V_{ds})}\right){\left(Z_L+\frac{L_g}{{\mu }_n{C}_{OX}W(V_g-V_{th}-V_{ds})}\right)}^2}{-\frac{L_g}{{\mu }_n{C}_{OX}W(V_g-V_{th}-V_{ds})}\cdot {\left(\frac{Z_L}{V_g-V_{th}-V_{ds}}\right)}^2(Z_L+Z_{OFF})}\text{\hspace{1em}(9)}$$
由(8)、(9)可以计算出1dB压缩点，如公式(10)所示：
P 1 d B = 10 log ⁡ 10 ( 1000 ⋅ ( 0.145 ∣ c 1 / c 3 ∣ / 2 ) 2 4 Z S ) d B m (10) P_{1dB}=10\log_{10}\left( \frac{1000\cdot\left(\sqrt{0.145|c_1/c_3|}/\sqrt2\right)^2}{4Z_S} \right)dBm \tag{10} P1dB​=10log10​ ​4ZS​1000⋅(0.145∣c1​/c3​∣ ​/2 ​)2​ ​dBm(10)

噪声系数

忽略正弦LO导致的ON-OFF状态混叠带来的噪声。其输出电压的噪声谱密度为 $v_n^2=8k{T}_0/g_{ds}$，其最终的噪声系数为如公式(11)所示：
$$\begin{array}{rl}F=& \frac{1}{g_c^2}+\frac{F_{MIX}}{g_c^2\cdot k{T}_0{R}_s}=\frac{1}{g_c^2}+\frac{8k{T}_0/g_{ds}}{g_c^2\cdot k{T}_0{R}_s}\\ \Rightarrow & SSBNF=10{\log }_{10}\left(\frac{1}{g_c^2}+\frac{2}{g_c^2\cdot g_{ds}\cdot R_s}\right)\end{array}\text{\hspace{1em}(11)}$$

测量与仿真结果

仿真得到的变频增益、1dB压缩点、噪声系数如图5所示。其仿真采用Cadence Spectre-RF软件，依次采用130nm-65nm工艺制程的高精度高频晶体管模型，并与其它论文结果进行了对比。本文还实测了一个130nm工艺的混频器，也在图5中标出来了。

定义 $FOM$ 来综合考量混频器的变频增益、1dB压缩点、噪声系数等指标，得到公式(12)
$$FO{M}_{MIXER}(dBm/Hz)=G_c-SSBNF+P_{1dB}-P_{CONSUMED}\text{\hspace{1em}(12)}$$
虽然无源混频器没有用使用直流电源，但是却采用了LO的能量，于是添加了 $P_{COMSUMED}=V_{DD}{I}_{DC}+P_{LO}$

---

AI解析

文章概述

本文研究了CMOS无源双平衡混频器的基本性能限制和扩展。通过分析单晶体管无源混频器的模型，进一步分析了双平衡混频器的性能。研究发现，随着CMOS工艺技术的发展和MOSFET器件的门长减小，FET-Quad混频器的性能参数接近其理想的基本限制。该研究为比较不同技术的混频器性能提供了必要的工具。

研究背景

本篇文章的研究背景是关于CMOS无源双平衡混频器的基本性能和尺寸的极限的研究。文章介绍了CMOS技术在无线收发器的模拟组件中取代双极性晶体管的趋势，并探讨了随着CMOS工艺尺寸缩小，无源双平衡混频器的性能指标如转换增益、1-dB压缩点和噪声系数等如何受到影响。研究表明，随着CMOS工艺技术的发展，无源双平衡混频器的架构将变得更加有利，并能够提供更好的性能。这一结论通过在CMOS 350nm到32nm工艺下设计的混频器的模拟和建模结果得到验证。文章还引入了混频器的性能评估指标（FOM_MIXER），以比较不同工艺尺寸下的性能。这篇论文可以帮助电路设计师和系统架构师找到适合其规格要求的工艺技术。

研究思路

本研究的研究问题是关于CMOS无源双平衡混频器的基本性能和尺寸的极限。研究通过分析无源双平衡混频器的性能指标，如变频增益、1-dB压缩点和SSB噪声系数，来探讨晶体管栅长的缩小对其性能的直接影响。研究还通过模拟和建模结果验证了随着CMOS工艺技术的发展，无源双平衡混频器架构将变得更有利并能进一步提高性能。此外，研究引入了混频器的性能评估指标（FOM_MIXER），用于比较不同工艺尺寸下的性能表现。通过本研究，电路设计师和系统架构师可以找到适合其规格要求的工艺技术。

研究的思路主要包括以下几个方面：

1. 首先，研究回顾了CMOS技术在无线收发器的模拟组件中取代双极性晶体管的发展历程，并介绍了CMOS无源双平衡混频器和有源双平衡混频器的优劣势。
2. 接着，研究分析了无源双平衡混频器的基本工作原理，包括使用CMOS技术构建的FET-Quad混频器的结构和工作方式。
3. 研究对无源双平衡混频器的性能进行了详细分析，包括电压转换增益、1-dB压缩点、IIP3和噪声系数等指标。通过建立模型和方程式，研究得出了这些性能指标与CMOS工艺尺寸缩放之间的关系。
4. 最后，研究引入了一个新的性能评估指标（FOM），综合考虑了转换增益、IIP3、1-dB压缩点和噪声系数等参数。这个指标可以帮助电路设计师和系统架构师选择适合其要求的工艺技术。
5. 通过以上研究思路和方法，本研究解决了关于CMOS无源双平衡混频器的性能极限和尺寸缩放的研究问题，并为电路设计师和系统架构师提供了选择合适工艺技术的参考依据。

研究结果

这篇文章主要研究了CMOS被动双平衡混频器的基本性能和尺寸极限。文章通过分析被动双平衡混频器的性能指标，如转换增益、1-dB压缩点和单边带噪声系数，展示了这些指标如何受到晶体管栅长缩放的直接影响。文章还介绍了一种混频器的性能评估指标（FOM_MIXER），用于比较不同工艺尺寸的性能。

文章通过理论分析、仿真和实测验证了模型的准确性。作者还通过在CMOS 350nm到32nm工艺下设计的混频器进行仿真和建模，验证了随着CMOS工艺技术的发展，被动双平衡混频器的架构将变得更有优势并具有改进的性能。

至于实验的假设论证，文章没有明确提到具体的实验，而是通过理论分析、仿真和建模来验证模型的准确性。因此，文章没有提供实验假设的论证结果。

研究结论与讨论

1、研究结论：本文的研究结论是随着CMOS工艺技术的发展和晶体管栅长的缩小，双平衡无源混频器的性能参数将达到理想的极限。通过模拟和建模结果验证了这一结论，并引入了混频器的性能评价指标（FOM_MIXER）来比较不同工艺的性能。

2、研究的创新性：本研究的创新之处在于对双平衡无源混频器的性能极限进行了分析，并提出了与工艺参数相关的新的性能评价指标。此外，通过模拟和建模验证了研究结论，为电路设计师和系统架构师选择合适的工艺技术提供了参考。

3、研究的不足之处：本研究的不足之处可能包括对其他混频器结构的比较不充分，以及对实际工艺的适应性的缺乏分析。此外，由于本文是基于理论和模拟结果的分析，可能存在与实际器件性能的差异。

4、研究展望：根据这项研究，后续可能的研究方向包括进一步探索不同混频器结构的性能极限和优化方法，以及与混频器性能相关的其他工艺参数的研究。此外，可以考虑将本研究扩展到更先进的工艺技术，并进行实际器件的测试和验证。

5、研究意义：本研究的理论意义在于揭示了双平衡无源混频器的性能极限和与工艺参数的关系，为混频器设计和工艺选择提供了指导。在实践意义上，本研究为电路设计师和系统架构师提供了选择合适工艺技术的依据，以满足系统规格要求并提高性能。

---

公式(2)变量解释：

• $R_{ON}$: 晶体管开启时的电阻。
• $r_{ds}$: 晶体管开启时的通态电阻。
• $L_g$: 晶体管的栅长。
• W: 晶体管的栅宽。
• ${\mu }_n$: n型沟道迁移率。
• $C_{OX}$: 栅氧化层电容密度。
• $V_g$: 晶体管的栅源电压。
• $V_{th}$: 晶体管的阈值电压。
• $V_{ds}$: 晶体管的漏极-源极电压
• $v_{RF}$: 射频信号的幅度。
• $g_c$: 晶体管的跨导。
• $(V_g-g_c\cdot v_{RF})-V_{th}-V_{ds}$: 得到晶体管工作时的电压。

公式(3)变量解释

• $Z_{OFF}$: 晶体管关闭时的阻抗。
• $C_{GS(V_{G}S=0)}$: 当晶体管的栅源电压为0时的栅源电容。
• $C_{GD(V_{G}S=0)}$: 当晶体管的栅源电压为0时的栅漏电容。
• ||: 表示并联。

公式(11)的变量解释

• $F_{MIX}$：混频器本身的噪声系数。
• k：玻尔兹曼常数。
• $T_0$：系统的参考温度。
• $R_s$：混频器输入端的源电阻。
• $g_{ds}$：混频器的跨导。

公式的第一部分 $1/g_c^2$ 表示了输入信号的转换增益的倒数，即输入信号功率的倒数。这部分表示了信号被混频器转换产生的信号增益。

第二部分 $\frac{F_{MIX}}{g_c^2\cdot k{T}_0{R}_s}$ 表示了混频器本身的噪声系数相对于输入信号的转换增益。这部分表示了混频器内部噪声对整体噪声系数的贡献。

通过组合这两部分，我们可以得到总体的噪声系数。

最后，公式通过引入SSB NF（单边带噪声系数），将噪声系数转化为以分贝为单位的值。

---

1. Linear Time Invariant，线性时不变系统 ↩︎

2. Linear Peroid Time Variant，线性周期时变系统 ↩︎

3. Woerlee, et al, “RF CMOS performance trends”, IEEE Trans. ED, vol.48, no.8, pp.1776-1782,. August 2001 ↩︎