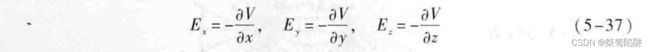【大学物理笔记】静电场
5.1 电荷的量子化 电荷守恒定律
电荷的量子化
一般认为汤姆孙是电子发现者。
电子电荷的绝对值的近似值:
e = 1.602 × 1 0 − 19 C e=1.602\times10^{-19}C e=1.602×10−19C
电荷守恒定律
不论系统内的电荷如何迁移,系统的电荷代数和保持不变。
5.2 库仑定律
在真空中,两个静止的点电荷之间的相互作用力,其大小与它们电荷的乘积成正比,与它们之间距离的二次方成反比;作用力的方向沿着两点电荷的连线,同号电荷相斥,异号电荷相吸。
假设现在真空中(低速)有两个静止点电荷 q 1 q_1 q1、 q 2 q_2 q2,用线段把它们连接起来,线段距离为 r \textbf{r} r,那么两点电荷受到相互作用力 F \textbf{F} F如此计算:
F = 1 4 π ϵ 0 q 1 q 2 r 2 e r \textbf{F}=\frac{1}{4π\epsilon_0}\frac{q_1q_2}{r^2}\textbf{e}_r F=4πϵ01r2q1q2er
一般计算时, ϵ 0 \epsilon_0 ϵ0取 8.85 × 1 0 − 12 C 2 ⋅ N − 1 ⋅ m − 2 8.85\times10^{-12} C^2·N^{-1}·m^{-2} 8.85×10−12C2⋅N−1⋅m−2。
当 q 1 、 q 2 q_1、q_2 q1、q2同号时,库仑力表现为斥力,反之则为引力。
5.3 电场强度
静电场
处于静电场中的电荷要受到电场力作用,并且当电荷在电场中运动时电场力也要对它做功。
从而,我们能够引出两个物理量:电场强度和电势。
电场强度
试验电荷必须是点电荷,且电量足够小。
电场强度计算公式:
E = F q 0 \textbf{E}=\frac{\textbf{F}}{q_0} E=q0F
它表明电场中某点处的电场强度 E \textbf{E} E等于位于该点处的单位试验电荷所受的电场力。
这里的电场力,我高中的时候经常有一个很奇怪的想法,那就是“电场是凭空产生的”,跟点电荷激发的电场独立开来。但是不是的。静电场它总是有一定量的静止点电荷激发的,哪怕匀强电场也是,就比如说附着了均匀电荷的板子,比如示波器,加速器。
位于该点就说明它已经受到了与电场电荷的相互作用力,而这一点在公式中体现出的是它与这个电场电荷的距离。
点电荷的电场强度
点电荷位于空间直角坐标系的原点O,设一试验电荷位于场点P,原点指向该点P的位矢为 r \textbf{r} r。
如果点电荷为正电荷(即 Q > 0 Q>0 Q>0), E E E的方向与 e r \textbf{e}_r er相同。
反之若为负电荷,则相反。(见书P164)
点电荷电场强度计算公式:
E = F q 0 = 1 4 π ϵ 0 Q r 2 e r \textbf{E}=\frac{\textbf{F}}{q_0}=\frac{1}{4π\epsilon_0}\frac{Q}{r^2}\textbf{e}_r E=q0F=4πϵ01r2Qer
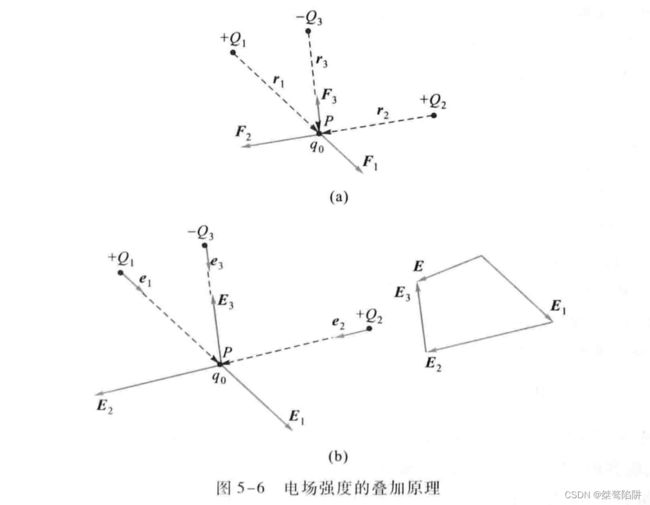
电场强度叠加原理
由力的叠加原理可得出电场强度叠加原理。
书上的例子:设真空中一点电荷系由 Q 1 , Q 2 Q_1,Q_2 Q1,Q2和 Q 3 Q_3 Q3三个点电荷组成,在场点P处放置一个试验电荷 q 0 q_0 q0,且 Q 1 , Q 2 Q_1,Q_2 Q1,Q2和 Q 3 Q_3 Q3到点P的位矢为 r 1 、 r 2 、 r 3 \textbf{r}_1、\textbf{r}_2、\textbf{r}_3 r1、r2、r3,若试验电荷收到三点电荷作用力为 F 1 、 F 2 、 F 3 \textbf{F}_1、\textbf{F}_2、\textbf{F}_3 F1、F2、F3,则由力的叠加原理叠加.
F = \textbf{F}= F= F 1 + F 2 + F 3 \textbf{F}_1+\textbf{F}_2+\textbf{F}_3 F1+F2+F3
其中,
F 1 = 1 4 π ϵ 0 q 0 Q 1 r 1 2 e 1 \textbf{F}_1=\frac{1}{4π\epsilon_0}\frac{q_0Q_1}{r_1^2}\textbf{e}_1 F1=4πϵ01r12q0Q1e1
F 2 = 1 4 π ϵ 0 q 0 Q 2 r 2 2 e 2 \textbf{F}_2=\frac{1}{4π\epsilon_0}\frac{q_0Q_2}{r_2^2}\textbf{e}_2 F2=4πϵ01r22q0Q2e2
F 3 = 1 4 π ϵ 0 q 0 Q 3 r 3 2 e 3 \textbf{F}_3=\frac{1}{4π\epsilon_0}\frac{q_0Q_3}{r_3^2}\textbf{e}_3 F3=4πϵ01r32q0Q3e3
由电场强度定义式得出P点电场强度:
E = F q 0 = F 1 q 0 + F 2 q 0 + F 3 q 0 \textbf{E}=\frac{\textbf{F}}{q_0}=\frac{\textbf{F}_1}{q_0}+\frac{\textbf{F}_2}{q_0}+\frac{\textbf{F}_3}{q_0} E=q0F=q0F1+q0F2+q0F3
于是,P点电场强度为:
E = 1 4 π ϵ 0 Q 1 r 1 2 e 1 + 1 4 π ϵ 0 Q 2 r 2 2 e 2 + 1 4 π ϵ 0 Q 3 r 3 2 e 3 \textbf{E}=\frac{1}{4π\epsilon_0}\frac{Q_1}{r_1^2}\textbf{e}_1+\frac{1}{4π\epsilon_0}\frac{Q_2}{r_2^2}\textbf{e}_2+\frac{1}{4π\epsilon_0}\frac{Q_3}{r_3^2}\textbf{e}_3 E=4πϵ01r12Q1e1+4πϵ01r22Q2e2+4πϵ01r32Q3e3
可知式中右边第一、二、三项分别代表 Q 1 、 Q 2 、 Q 3 Q_1、Q_2、Q_3 Q1、Q2、Q3各自存在时点P的电场强度,即:
E 1 = 1 4 π ϵ 0 Q 1 r 1 2 e 1 \textbf{E}_1=\frac{1}{4π\epsilon_0}\frac{Q_1}{r_1^2}\textbf{e}_1 E1=4πϵ01r12Q1e1
E 2 = 1 4 π ϵ 0 Q 2 r 2 2 e 2 \textbf{E}_2=\frac{1}{4π\epsilon_0}\frac{Q_2}{r_2^2}\textbf{e}_2 E2=4πϵ01r22Q2e2
E 3 = 1 4 π ϵ 0 Q 3 r 3 2 e 3 \textbf{E}_3=\frac{1}{4π\epsilon_0}\frac{Q_3}{r_3^2}\textbf{e}_3 E3=4πϵ01r32Q3e3
所以有:
E = E 1 + E 2 + E 3 \textbf{E}=\textbf{E}_1+\textbf{E}_2+\textbf{E}_3 E=E1+E2+E3
式中表明,三个点电荷在点P处激起的的电场强度等于各个点电荷单独存在时该处电场强度的矢量和。
试推广至任意数量的点电荷所组成的点电荷系,得出一普遍结论:
点电荷系所激发的电场中的某点处的电场强度等于各个点电荷单独存在时对该点所激起的电场强度的矢量和。此即为电场强度的叠加原理。
其数学表达式:
E = ∑ i = 1 n E i = 1 4 π ϵ 0 ∑ i = 1 n Q i r i 2 e r \textbf{E}=\sum_{i=1}^{n}\textbf{E}_i=\frac{1}{4π\epsilon_0}\sum_{i=1}^{n}\frac{Q_i}{r_i^2}\textbf{e}_r E=∑i=1nEi=4πϵ01∑i=1nri2Qier
据此原理,我们可以计算连续分布的电荷系的电场强度,用到积分工具:
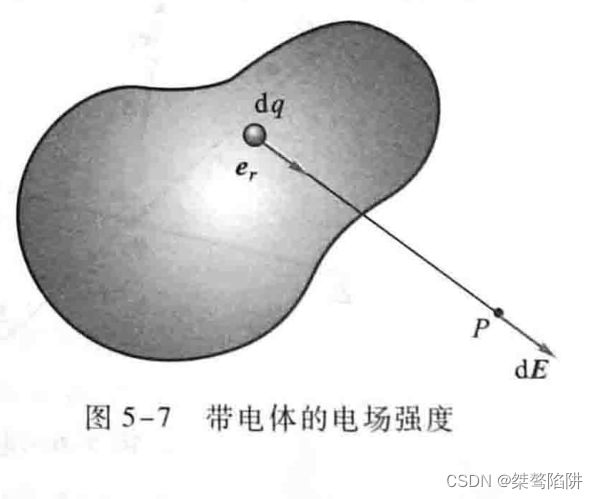
设有一体积为 V V V的电荷连续分布的带电体,在其中取一电荷元d q q q,
那么设这一点P上,电荷元所受的电场强度为d E E E
d E = 1 4 π ϵ 0 d q r 2 e r \textbf{E}=\frac{1}{4π\epsilon_0}\frac{dq}{r^2}\textbf{e}_r E=4πϵ01r2dqer
可得电荷系(连续分布电荷)在点P处的电场强度 E \textbf{E} E为:
E = ∫ V d E = ∫ V 1 4 π ϵ 0 e r r 2 d q \textbf{E}=\int_Vd\textbf{E}=\int_V\frac{1}{4π\epsilon_0}\frac{\textbf{e}_r}{r^2}dq E=∫VdE=∫V4πϵ01r2erdq,若 d V dV dV为电荷元d q q q的体积元, ρ \rho ρ为其电荷体密度,则d q q q= ρ \rho ρd V V V,于是,上式亦可写成:
E = ∫ V 1 4 π ϵ 0 ρ e r r 2 d V \textbf{E}=\int_V\frac{1}{4π{\epsilon}_0}\frac{\rho\textbf{e}_r}{r^2}dV E=∫V4πϵ01r2ρerdV
对于电荷连续分布的线带电体和面带电体来说,电荷元d q q q分别为d q q q= λ \lambda λd l l l、d q q q= σ \sigma σd S S S.
对上两式积分,它们的电场强度易于推知。
电偶极子的电场强度
电偶极子:由两个电荷量相等,符号相反,相距为 r 0 r_0 r0的点电荷+q、-q构成的电荷系成为电偶极子。
从-q指向+q的矢量 r 0 \textbf{r}_0 r0为电偶极子的轴, q r 0 q\textbf{r}_0 qr0称为电偶极子的电偶极矩(简称电矩),用符号 p \textbf{p} p表示,有 p = q r 0 \textbf{p}=q\textbf{r}_0 p=qr0.
(1)取电偶极子轴线的中点为坐标原点O,沿极轴的延长线为Ox轴,轴上任一点A距离原点O的距离为 x x x,得电场强度如下图所示:
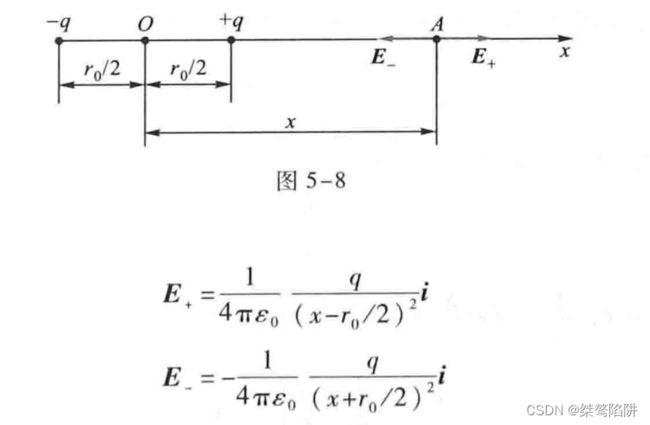
上两式表明, E + \textbf{E}_+ E+和 E − \textbf{E}_- E−的方向都沿Ox轴,但方向相反,由电场强度叠加原理可知,点A处的 E \textbf{E} E为
E = E + + E − = q 4 π ϵ 0 2 x r 0 ( x 2 − r 0 2 / 4 ) 2 i \textbf{E}=\textbf{E}_++\textbf{E}_-=\frac{q}{4π\epsilon_0}\frac{2xr_0}{(x^2-r_0^2/4)^2}\textbf{i} E=E++E−=4πϵ0q(x2−r02/4)22xr0i.
5.4 电场强度通量 高斯定理
1.电场线
电场线总是始于正电荷,终止于负电荷,不形成闭合曲线(指一条时)。
任何两条电场线都不能相交,这是因为电场中每一点处的电场强度只能有一个确定的方向。
电场线在空间中的密度能表示电场强度的大小。
对电场线的密度作如下规定:在电场中任一点,想象地做一个面积元dS,并使它与该点处的 E \textbf{E} E垂直,则通过面积元dS的电场线数dN与该点的 E \textbf{E} E的大小有如下关系:
d N d S = d E \frac{dN}{dS}=dE dSdN=dE
2.电场强度通量
通过电场中某一个面的电场线数目,称作这个面的电场强度通量。
匀强电场中电场强度通量 ϕ \phi ϕ,电场线密度处处相等:
ϕ e = E S \phi_e=ES ϕe=ES
匀强电场中 E \textbf{E} E与平面S不垂直:
ϕ e = E S c o s θ \phi_e=EScos\theta ϕe=EScosθ
非匀强电场,且面S是任意曲面:
ϕ e = ∫ S E c o s θ d S \phi_e=\int_SEcos\theta dS ϕe=∫SEcosθdS
即
ϕ e = ∫ S E d S \phi_e=\int_S\textbf{E} d\textbf{S} ϕe=∫SEdS
3.高斯定理
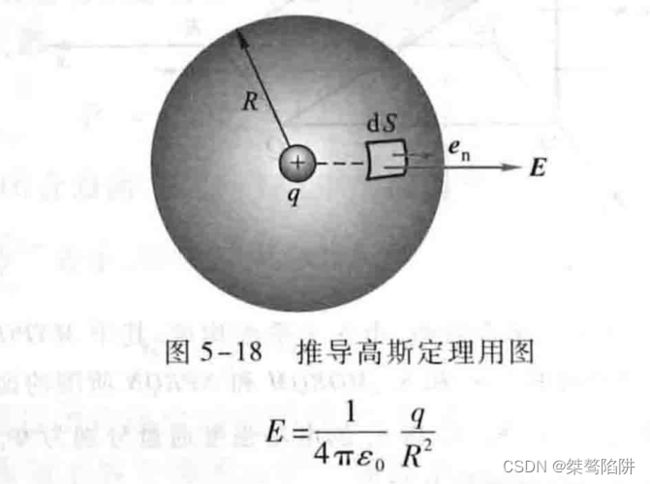
设真空中有一个正点电荷q,被置于半径为R的球面中心O,由点电荷电场强度公式可知,球面上各点电场强度 E \textbf{E} E的大小均等于:
d ϕ e = E d S = E d S = 1 4 π ϵ 0 q R 2 d S d\phi_e=\textbf{E}dS=EdS=\frac{1}{4π\epsilon_0}\frac{q}{R^2}dS dϕe=EdS=EdS=4πϵ01R2qdS
于是通过整个球面的电场强度通量为:
ϕ e = ∮ S d ϕ e = ∮ S E d S = 1 4 π ϵ 0 q R 2 ∮ S d S = 1 4 π ϵ 0 q R 2 4 π R 2 \phi_e=\oint_Sd\phi_e=\oint_S\textbf{E}d\textbf{S}=\frac{1}{4π\epsilon_0}\frac{q}{R^2}\oint_SdS=\frac{1}{4π\epsilon_0}\frac{q}{R^2}4πR^2 ϕe=∮Sdϕe=∮SEdS=4πϵ01R2q∮SdS=4πϵ01R2q4πR2
得(高斯定理):
ϕ e = ∮ S E d S = q ϵ 0 \phi_e=\oint_S\textbf{E}d\textbf{S}=\frac{q}{\epsilon_0} ϕe=∮SEdS=ϵ0q
真空中静电场的高斯定理(点电荷位于闭合曲面之外):
∮ E d S = 1 ϵ 0 ∑ i = 1 n q i n \oint\textbf{E}d\textbf{S}=\frac{1}{\epsilon_0}\sum^n_{i=1} q_{in} ∮EdS=ϵ01∑i=1nqin
5.6 静电场的环路定理 电势能
1.静电场力所做的功
W = q 0 ∫ l E d l W=q_0\int_l\textbf{E}d\textbf{l} W=q0∫lEdl
可得一结论:静电场对其中点电荷所做的功只与其 q 0 q_0 q0及路径起点终点有关,与其路径形状无关。
2.静电场的环路定理
点电荷沿闭合路径移动一周,电场力做功为0,即:
q 0 ∮ l E d l = 0 q_0\oint_l\textbf{E}d\textbf{l}=0 q0∮lEdl=0
上式成立的条件必须是
∮ l E d l = 0 \oint_l\textbf{E}d\textbf{l}=0 ∮lEdl=0
3.电势能
W A B = E p A − E p B = − ( E p B − E p A ) W_{AB}=E_{pA}-E_{pB}=-(E_{pB}-E_{pA}) WAB=EpA−EpB=−(EpB−EpA)
选取一个电势能参考点。设该点的电势能为零,这样,若 E p B = 0 E_{pB}=0 EpB=0,则有:
E p A = q 0 ∫ A B E d l E_{pA}=q_0\int_{AB}\textbf{E}d\textbf{l} EpA=q0∫ABEdl
5.7 电势
如取
V A = E p A / q 0 V_{A}=E_{pA}/q_0 VA=EpA/q0
V B = E p B / q 0 V_{B}=E_{pB}/q_0 VB=EpB/q0
称 V A V_A VA和 V B V_B VB分别为点A和点B的电势。
V A = ∫ A B E d l + V B V_{A}=\int_{AB}\textbf{E}d\textbf{l}+V_{B} VA=∫ABEdl+VB
若B在无限远处,则 E p B = 0 E_{pB}=0 EpB=0, V B = 0 V_B=0 VB=0,电场中点A的电势为:
V A = ∫ ∞ A E d l V_A=\int_{\infty A}\textbf{E}d\textbf{l} VA=∫∞AEdl
表明电场中某一点A的电势 V A V_A VA,在数值上等于单位正试验电荷从A移到无限远处时,静电场力所做的功。
亦可写成:
V A = − ∫ A ∞ E d l V_A=-\int_{ A\infty}\textbf{E}d\textbf{l} VA=−∫A∞Edl
两点电势差可写成:
U A B = V A − V B = − ( V B − V A ) = ∫ A B E d l U_{AB}=V_A-V_B=-(V_B-V_A)=\int_{AB}\textbf{E}d\textbf{l} UAB=VA−VB=−(VB−VA)=∫ABEdl
2.点电荷电场的电势
V = ∫ r ∞ E d l = q 4 π ϵ 0 1 r V=\int^\infty_r\textbf{E}d\textbf{l}=\frac{q}{4π\epsilon_0}\frac{1}{r} V=∫r∞Edl=4πϵ0qr1
当q>0时,电场中各点电势都是正值,反之则都为负。
3.电势的叠加原理
点电荷系所激发的电场中某点的电势,等于各点电荷单独存在时在该点建立的电势的代数和。
V A = ∑ i = 1 n 1 4 π ϵ 0 q i r i V_A=\sum^n_{i=1}\frac{1}{4π\epsilon_0}\frac{q_i}{r_i} VA=∑i=1n4πϵ01riqi
5.8 电场强度和电势梯度
1.等势面
某点电场强度与通过该点的等势面垂直。
q E d l = 0 q\textbf{E}d\textbf{l}=0 qEdl=0
规定:电场中任意两个相邻的=等势面之间的电势差都相等。
2.电场强度与电势梯度
电场中某一点的电场强度沿任一方向的分量,等于这一点的电势沿该方向的电势变化率的负值。
E l = d V d l E_l=\frac{dV}{dl} El=dldV
E的方向总是从高电势指向低电势。
E = − d V d l n e n \textbf{E}=-\frac{dV}{dl_n}\textbf{e}_n E=−dlndVen
在空间直角坐标系中,电场强度在x,y,z这三个方向的分量分别为:
推论:电场强度 E \textbf{E} E等于电势梯度的负值。