【算法提升—力扣每日一刷】五日总结【12/13--12/17】
文章目录
-
-
- 2023/12/13
-
- 力扣每日一刷:[141. (判断)环形链表](https://leetcode.cn/problems/linked-list-cycle/)
- 力扣今日两刷:[142. (找入环点)环形链表 II](https://leetcode.cn/problems/linked-list-cycle-ii/)
- 判断环形链表(找入环点)
- 2023/12/14
-
- 力扣每日一刷:[88. 合并两个有序数组](https://leetcode.cn/problems/merge-sorted-array/)
- 2023/12/15
-
- 力扣每日一刷:[102. 二叉树的层序遍历](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
- 2023/12/16
-
- 每日力扣:[237. 删除链表中的节点](https://leetcode.cn/problems/delete-node-in-a-linked-list/)
- 2023/12/17
-
- 每日力扣:[160. 相交链表](https://leetcode.cn/problems/intersection-of-two-linked-lists/)
- 力扣每五日一总结【12/13--12/17】
- 2023/12/13
- 2023/12/14
- 2023/12/15
- 2023/12/16
- 2023/12/17
-

2023/12/13
力扣每日一刷:141. (判断)环形链表
给你一个链表的头节点
head,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ,则返回
true。 否则,返回false。示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。提示:
- 链表中节点的数目范围是
[0, 104]-105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。**进阶:**你能用
O(1)(即,常量)内存解决此问题吗?
//判断环形链表
public class E10Leedcode141 {
//思路:每次乌龟走一步,兔子走两步,如果兔子能追上乌龟,则证明链表中有环存在,否则当兔子走到链表尽头,则证明无环存在
public boolean hasCycle(ListNode head) {
ListNode p1 = head;//乌龟
ListNode p2 = head;//兔子
while (p2 != null && p2.next != null) {
p2 = p2.next.next;
p1 = p1.next;
if (p2 == p1) {
return true;
}
}
return false;
}
}
这段代码定义了一个名为
E10Leedcode141的类,其中包含一个名为hasCycle的方法,用于判断链表中是否存在环。方法的主要思路是:每次让乌龟节点(p1)走一步,兔子节点(p2)走两步。当兔子追上乌龟时,说明链表中存在环;当兔子到达链表末尾时,说明链表中不存在环。
具体实现如下:
- 初始化两个指针p1和p2,分别指向链表的头节点head。
- 进入循环,当p2不为空且p2的下一个节点不为空时,让p2每次走两步,p1每次走一步。
- 在循环中,如果p2和p1相遇(p2 == p1),说明链表中存在环,返回true。
- 当兔子到达链表末尾(p2 == null或p2.next == null)时,说明链表中不存在环,返回false。
总之,这段代码通过判断兔子追上乌龟和兔子到达链表末尾的情况,来判断链表中是否存在环。
//哈希表
public class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> seen = new HashSet<ListNode>();
while (head != null) {
if (!seen.add(head)) {
return true;
}
head = head.next;
}
return false;
}
}
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可。
力扣今日两刷:142. (找入环点)环形链表 II
给定一个链表的头节点
head,返回链表开始入环的第一个节点。 如果链表无环,则返回null。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。如果pos是-1,则在该链表中没有环。注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。提示:
- 链表中节点的数目范围在范围
[0, 104]内-105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引**进阶:**你是否可以使用
O(1)空间解决此题?
//判断环形链表(找入环点)
public class E11Leedcode142 {
public ListNode detectCycle(ListNode head) {
ListNode p1 = head;//兔子
ListNode p2 = head;//乌龟
while (p2 != null && p2.next != null) {
p2 = p2.next.next;
p1 = p1.next;
if (p2 == p1) {
//相遇,从相遇点开始,让乌龟回到起点,让乌龟和兔子同时移动,再次相遇的节点就是入环点
p2 = head;
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}
return null;
}
}
判断环形链表(找入环点)
该算法利用快慢指针的思想来判断链表是否有环,并且找出环的入口点。
具体步骤如下:
- 定义两个指针p1和p2,初始时都指向链表的头节点head。
- 同时移动p1和p2,其中p1每次移动一步,p2每次移动两步,直到p2到达链表尾部或者p2的下一个节点为null。
- 如果p2到达链表尾部,说明链表不包含环,返回null。
- 如果p2的下一个节点为null,说明链表不包含环,返回null。
- 如果p2等于p1,说明链表包含环。此时将p2重新指向链表头部,然后p1和p2同时移动,每次移动一步,直到p1等于p2。
- 返回p1,即为环的入口点。
时间复杂度为O(n),空间复杂度为O(1)。
本题以及下题,实际是 Floyd’s Tortoise and Hare Algorithm (Floyd 龟兔赛跑算法)[^15]
除了 Floyd 判环算法外,还有其它的判环算法,详见 https://en.wikipedia.org/wiki/Cycle_detection
如果链表上存在环,那么在环上以不同速度前进的两个指针必定会在某个时刻相遇。算法分为两个阶段
阶段1
- 龟一次走一步,兔子一次走两步
- 当兔子能走到终点时,不存在环
- 当兔子能追上龟时,可以判断存在环
阶段2
- 从它们第一次相遇开始,龟回到起点,兔子保持原位不变
- 龟和兔子一次都走一步
- 当再次相遇时,地点就是环的入口
为什么呢?
- 设起点到入口走 a 步(本例是 7),绕环一圈长度为 b(本例是 5),
- 那么从起点开始,走 a + 绕环 n 圈,都能找到环入口
- 第一次相遇时
- 兔走了 a + 绕环 n 圈(本例 2 圈) + k,k 是它们相遇距环入口位置(本例 3,不重要)
- 龟走了 a + 绕环 n 圈(本例 0 圈) + k,当然它绕的圈数比兔少
- 兔走的距离是龟的两倍,所以龟走的 = 兔走的 - 龟走的 = 绕环 n 圈
- 而前面分析过,如果走 a + 绕环 n 圈,都能找到环入口,因此从相遇点开始,再走 a 步,就是环入口
2023/12/14
力扣每日一刷:88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组
nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中,使合并后的数组同样按 非递减顺序 排列。**注意:**最终,合并后数组不应由函数返回,而是存储在数组
nums1中。为了应对这种情况,nums1的初始长度为m + n,其中前m个元素表示应合并的元素,后n个元素为0,应忽略。nums2的长度为n。示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
//方法一:迭代 双指针
public void merge(int[] nums1, int m, int[] nums2, int n) {
int[] nums3 = new int[m + n];
int i = 0, j = 0, k = 0;
//当i和j都小于m和n时,循环
while (i < m && j < n) {
//当nums1[i]小于nums2[j]时,将nums1[i]放入nums3[k]
if (nums1[i] < nums2[j]) {
nums3[k] = nums1[i];
k++;
i++;
//当nums1[i]大于等于nums2[j]时,将nums2[j]放入nums3[k]
} else {
nums3[k] = nums2[j];
k++;
j++;
}
}
//当i小于m时,将nums1[i]放入nums3[k]
while (i < m) {
nums3[k] = nums1[i];
k++;
i++;
}
//当j小于n时,将nums2[j]放入nums3[k]
while (j < n) {
nums3[k] = nums2[j];
k++;
j++;
}
//将nums3复制到nums1
System.arraycopy(nums3, 0, nums1, 0, m + n);
}
这段代码是Java语言实现的归并排序算法中的合并部分。归并排序是一种分治算法,它将数组分成两个子数组,然后递归地将它们排序,最后将它们合并成一个有序的数组。
以下是代码的详细解释:
- 定义一个长度为
m + n的新数组nums3,用于存储合并后的有序数组。- 定义三个指针
i、j和k,分别指向nums1、nums2和nums3的当前元素。- 使用一个
while循环,当i和j都小于m和n时,循环继续。- 在循环中,首先比较
nums1[i]和nums2[j]的大小。如果nums1[i]小于nums2[j],则将nums1[i]放入nums3[k],并将i和k分别加1。否则,将nums2[j]放入nums3[k],并将j和k分别加1。- 当
i小于m时,将nums1[i]放入nums3[k],并将i和k分别加1。- 当
j小于n时,将nums2[j]放入nums3[k],并将j和k分别加1。- 使用
System.arraycopy()方法将nums3复制到nums1。总之,这段代码实现了将两个已排序的数组合并成一个已排序的数组,它的时间复杂度为O(m + n),空间复杂度为O(m + n)。
//迭代:逆向双指针
public void merge3(int[] nums1, int m, int[] nums2, int n) {
int k = m + n - 1;
int i = m - 1;
int j = n - 1;
//当i和j都大于等于0时,比较nums1[i]和nums2[j],将较大的值放入nums1[k]
while (i >= 0 && j >= 0) {
if (nums1[i] > nums2[j]) {
nums1[k] = nums1[i];
k--;
i--;
} else {
nums1[k] = nums2[j];
k--;
j--;
}
}
//当i小于0时,将nums2中的值放入nums1
while (i>=0){
nums1[k] = nums1[i];
k--;
i--;
}
//当j小于0时,将nums1中的值放入nums1
while (j>=0){
nums1[k] = nums2[j];
k--;
j--;
}
}
这段代码是用于合并两个已排序的整数数组nums1和nums2的函数。函数的输入参数是两个整数数组nums1和nums2,以及它们的长度m和n。函数的目的是将两个数组合并成一个已排序的数组,即将nums2中的元素添加到nums1的末尾,然后对整个数组进行排序。
函数采用迭代方法,使用逆向双指针法。从两个数组的末尾开始,比较两个数组的元素,将较大的元素放入一个新的数组nums1的末尾。这样,每次循环后,nums1的合并进度会逐渐向前。当其中一个数组的元素遍历完后,将另一个数组剩余的元素依次添加到nums1的末尾。
以下是代码的详细解释:
- 首先,计算合并后数组的长度k,即m+n-1。
- 初始化两个指针i和j,分别指向数组nums1和nums2的末尾。
- 使用一个while循环,当i和j都大于等于0时,比较nums1[i]和nums2[j],将较大的值放入nums1[k]:
a. 如果nums1[i] > nums2[j],将nums1[i]放入nums1[k],然后将k减1,将i减1。
b. 如果nums1[i] <= nums2[j],将nums2[j]放入nums1[k],然后将k减1,将j减1。- 当i小于0时,将nums2中的值放入nums1。这是因为在while循环的终止条件中,i和j必须都大于等于0,因此当i小于0时,说明nums1的元素已经遍历完了,需要将nums2剩余的元素添加到nums1的末尾。
- 当j小于0时,将nums1中的值放入nums1。这是因为在while循环的终止条件中,i和j必须都大于等于0,因此当j小于0时,说明nums2的元素已经遍历完了,需要将nums1剩余的元素添加到nums1的末尾。
总之,这段代码实现了将两个已排序的整数数组合并成一个已排序的数组,即实现了归并排序算法中的“归并”过程。
//方法二:递归
public static void merge2(int[] nums1, int m, int[] nums2, int n) {
//将nums2中的元素复制到nums1后面空着的位置中
System.arraycopy(nums2, 0, nums1, m, n);
//创建一个新的数组
int[] nums3 = new int[m + n];
//调用merge方法,将nums1和nums3合并
merge(nums1, 0, m - 1, m, m + n - 1, nums3, 0);
//将合并后的结果复制到nums1中
System.arraycopy(nums3, 0, nums1, 0, n + m);
}
private static void merge(int[] arr, int i, int iEnd, int j, int jEnd, int[] arr2, int k) {
//如果i大于iEnd,则将arr中的元素复制到arr2中
if (i > iEnd) {
System.arraycopy(arr, j, arr2, k, jEnd - j + 1);
return;
}
//如果j大于jEnd,则将arr中的元素复制到arr2中
if (j > jEnd) {
System.arraycopy(arr, i, arr2, k, iEnd - i + 1);
return;
}
//如果arr[i]小于arr[j],则将arr[i]复制到arr2中
if (arr[i] < arr[j]) {
arr2[k] = arr[i];
//递归调用merge方法,将arr[i+1]和arr[j]合并
merge(arr, i + 1, iEnd, j, jEnd, arr2, k + 1);
} else {
//将arr[j]复制到arr2中
arr2[k] = arr[j];
//递归调用merge方法,将arr[i]和arr[j+1]合并
merge(arr, i, iEnd, j + 1, jEnd, arr2, k + 1);
}
}
这段代码是Java中实现归并排序的一个方法。归并排序是一种分治算法,它将数组分成两个子数组,然后对这两个子数组进行排序,最后将排序后的子数组合并成一个有序的数组。
方法二:递归
- 定义一个名为merge2的静态方法,接受两个整数数组nums1和nums2以及它们的长度m和n作为参数。
- 首先,将nums2中的元素复制到nums1中。这里使用了System.arraycopy方法,这是一个高效的数组复制方法。
- 创建一个新的数组nums3,长度为m + n。
- 调用merge方法,将nums1和nums3合并。merge方法也是一个静态方法,它接受五个参数:nums1、nums1的起始索引i、nums1的结束索引iEnd、nums3的起始索引k和nums3的结束索引m + n - 1。
- 将合并后的结果复制到nums1中。这里使用了System.arraycopy方法,这也是一个高效的数组复制方法。
2023/12/15
力扣每日一刷:102. 二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-1000 <= Node.val <= 1000
public List<List<Integer>> levelOrder(TreeNode root) {
// 存储结果
List<List<Integer>> result = new ArrayList<>();
// 如果根节点为空,则直接返回结果
if (root == null) {
return result;
}
// 创建一个队列
Queue<TreeNode> queue = new LinkedList<>();
// 将根节点放入队列
queue.offer(root);
// 记录每一层的节点个数
int c1 = 1;//每一层节点个数
// 当队列不为空时
while (!queue.isEmpty()) {
// 记录下一层节点个数
int c2 =0;//下一层节点个数
// 创建一个存储每一层节点的列表
List<Integer> lever = new ArrayList<>();
// 遍历每一层节点
for (int i = 0; i < c1; i++) {
// 从队列中取出一个节点
TreeNode node = queue.poll();
// 将节点的值添加到列表中
lever.add(node.val);
// 如果该节点有左子节点,则将左子节点放入队列
if(node.left!=null){
queue.offer(node.left);
c2++;
}
// 如果该节点有右子节点,则将右子节点放入队列
if(node.right!=null){
queue.offer(node.right);
c2++;
}
}
// 更新每一层节点个数
c1 = c2;
// 将每一层节点列表添加到结果中
result.add(lever);
}
// 返回结果
return result;
}
这段Java代码定义了一个名为
levelOrder的方法,该方法接收一个TreeNode类型的参数root,并返回一个包含整数的列表列表。列表的每个元素都是一个整数列表,表示二叉树的同一层上的节点值。以下是代码的详细解释:
- 创建一个名为
result的列表,用于存储结果。- 如果根节点为空,直接返回结果。
- 创建一个名为
queue的双向队列,用于存储节点。- 将根节点放入队列。
- 初始化一个计数器
c1,用于记录每一层的节点个数。- 进入一个循环,当队列不为空时:
a. 初始化一个计数器c2,用于记录下一层节点的个数。
b. 创建一个名为lever的列表,用于存储当前层的节点值。
c. 遍历每一层的所有节点(循环c1次):
i. 从队列中取出一个节点。
ii. 将节点的值添加到lever列表中。
iii. 如果该节点的左子节点不为空,则将左子节点放入队列。
iv. 如果该节点的右子节点不为空,则将右子节点放入队列。
d. 更新c1为c2,表示下一层的节点数。
e. 将lever列表添加到结果列表result中。- 返回结果列表
result。总之,这段代码的主要目的是层次遍历二叉树,并将同一层上的节点值存储在列表中。
2023/12/16
每日力扣:237. 删除链表中的节点
有一个单链表的 head,我们想删除它其中的一个节点 node。
给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。
链表的所有值都是 唯一的,并且保证给定的节点 node 不是链表中的最后一个节点。
删除给定的节点。注意,删除节点并不是指从内存中删除它。这里的意思是:
- 给定节点的值不应该存在于链表中。
- 链表中的节点数应该减少 1。
node前面的所有值顺序相同。node后面的所有值顺序相同。
自定义测试:
- 对于输入,你应该提供整个链表
head和要给出的节点node。node不应该是链表的最后一个节点,而应该是链表中的一个实际节点。 - 我们将构建链表,并将节点传递给你的函数。
- 输出将是调用你函数后的整个链表。
示例 1:
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:指定链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9
示例 2:
输入:head = [4,5,1,9], node = 1
输出:[4,5,9]
解释:指定链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9
提示:
- 链表中节点的数目范围是
[2, 1000] -1000 <= Node.val <= 1000- 链表中每个节点的值都是 唯一 的
- 需要删除的节点
node是 链表中的节点 ,且 不是末尾节点
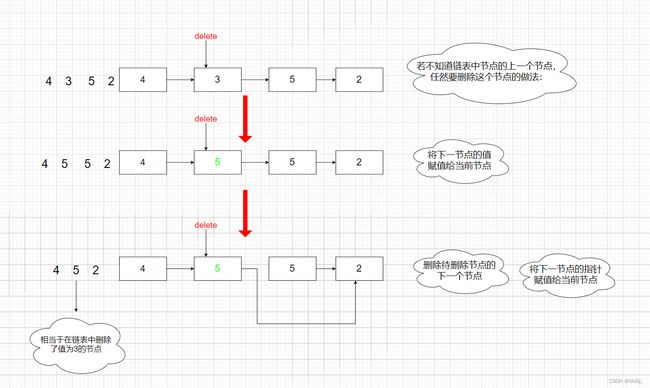
//删除节点
public void deleteNode(ListNode node) {
//将下一个节点的值赋值给当前节点
node.val = node.next.val;
//将下一个节点的指针赋值给当前节点
node.next = node.next.next;
}
图示:
2023/12/17
每日力扣:160. 相交链表
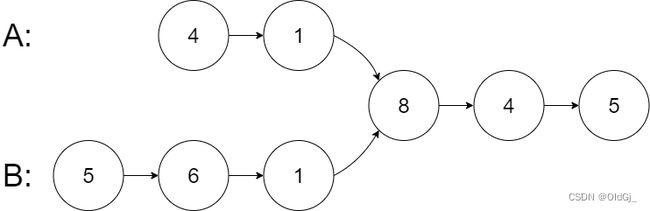
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
// 获取相交节点 双指针
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 定义两个指针p1和p2,分别指向headA和headB
ListNode p1 = headA;
ListNode p2 = headB;
// 循环遍历,当p1和p2相等时,返回p1
while (true) {
if (p1 == p2) {
return p1;
}
// 如果p1指向空,则指向headB
if (p1 == null) {
p1 = headB;
} else {
p1 = p1.next;
}
// 如果p2指向空,则指向headA
if (p2 == null) {
p2 = headA;
} else {
p2 = p2.next;
}
}
}
双指针:
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> visited = new HashSet<ListNode>();
ListNode temp = headA;
while (temp != null) {
visited.add(temp);
temp = temp.next;
}
temp = headB;
while (temp != null) {
if (visited.contains(temp)) {
return temp;
}
temp = temp.next;
}
return null;
}
}
哈希表:
力扣每五日一总结【12/13–12/17】
2023/12/13
141. (判断)环形链表
方法一:快慢双指针,思路:
每次让乌龟节点(p1)走一步,兔子节点(p2)走两步。当兔子追上乌龟时,说明链表中存在环;当兔子到达链表末尾时,说明链表中不存在环。
具体实现如下:
- 初始化两个指针p1和p2,分别指向链表的头节点head。
- 进入循环,当p2不为空且p2的下一个节点不为空时,让p2每次走两步,p1每次走一步。
- 在循环中,如果p2和p1相遇(p2 == p1),说明链表中存在环,返回true。
- 当兔子到达链表末尾(p2 == null或p2.next == null)时,说明链表中不存在环,返回false。
方法二:哈希表,思路:
遍历所有的节点,使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可。
142. (找入环点)环形链表 II
方法一:Floyd’s Tortoise and Hare Algorithm (Floyd 龟兔赛跑算法)
如果链表上存在环,那么在环上以不同速度前进的两个指针必定会在某个时刻相遇。算法分为两个阶段
阶段1
- 龟一次走一步,兔子一次走两步
- 当兔子能走到终点时,不存在环
- 当兔子能追上龟时,可以判断存在环
阶段2
- 从它们第一次相遇开始,龟回到起点,兔子保持原位不变
- 龟和兔子一次都走一步
- 当再次相遇时,地点就是环的入口
为什么呢?
- 设起点到入口走 a 步(本例是 7),绕环一圈长度为 b(本例是 5),
- 那么从起点开始,走 a + 绕环 n 圈,都能找到环入口
- 第一次相遇时
- 兔走了 a + 绕环 n 圈(本例 2 圈) + k,k 是它们相遇距环入口位置(本例 3,不重要)
- 龟走了 a + 绕环 n 圈(本例 0 圈) + k,当然它绕的圈数比兔少
- 兔走的距离是龟的两倍,所以龟走的 = 兔走的 - 龟走的 = 绕环 n 圈
- 而前面分析过,如果走 a + 绕环 n 圈,都能找到环入口,因此从相遇点开始,再走 a 步,就是环入口
2023/12/14
88. 合并两个有序数组
方法一:正序双指针,思路:
迭代两数组,比较两数组中的值,将两数组中较小的值放入新数组中,直到两数组中某一个元素较少的数组被迭代完毕,判断如果有数组中仍有未迭代的元素**(指针小于数组长度)**,将未迭代元素依次放入新数组中。
方法二:逆序双指针,(合理利用数组1中后n个元素的位置)思路:
与正序迭代类似,只是从数组最后一个元素开始迭代,依次将元素值比较大的元素放入新数组中(逆序放),此方法不需要开辟新的数组空间存放合并后的数组,空间复杂度为O( 1 )。
方法三:递归,思路:
将数组2先通过System.Arraycope()方法赋值到数组1中后n个位置,接着递归调用merge函数,该函数是将数组1分为两个部分,每次递归分别比较两个部分中哪个部分的值更小,将更小的元素赋值给一个新数组3,接着递归调用,参数传入已经赋值元素的下一个元素,直到某一部分元素全部赋值到新数组,则将另一部分也依次赋值到新数组中。
2023/12/15
102. 二叉树的层序遍历
方法一:队列 思路
二叉树的层序遍历使用队列的数据结构,遍历每一层时,设置一个计数器来计数每一层的节点个数
,依次遍历这一层的每一个节点,并使其出队,记录在一个集合中,如果当前节点的左右孩子不为空,则将其孩子节点加入队列,计数器加一,循环上述即可完成层序遍历。
2023/12/16
237. 删除链表中的节点
方法一:和下一节点互换,删除下一节点
删除链表中的节点的常见的方法是定位到待删除节点的上一个节点,修改上一个节点的next指针,使其指向待删除节点的下一个节点,即可完成删除操作。
这道题中,传入的参数nod为要被删除的节点,无法定位到该节点的上一个节点。注意到要被删除的节点不是链表的末尾节点,因此
node.next不为空,可以通过对node和node.net进行操作实现删除节点。在给定节点node的情况下,可以通过修改node的net指针的指向,删除node的下一个节点。但是题目要求删除node,为了达到删除node的效果,只要在删除节点之前,将node的节点值修改为
node.next的节点值即可。例如,给定链表4→5→1→9,要被删除的节点是5,即链表中的第2个节点。可以
通过如下两步操作实现删除节点的操作。
1.将第2个节点的值修改为第3个节点的值,即将节点5的值修改为1,此时链表如
下:
4→1→1→9
2.删除第3个节点,此时链表如下:
4→1→9
达到删除节点5的效果。2023/12/17
160. 相交链表