数据结构:KMP算法
1.何为KMP算法
KMP算法是由Knuth、Morris和Pratt三位学者发明的,所以取了三位学者名字的首字母,叫作KMP算法。
2.KMP的用处
KMP主要用于字符串匹配的问题,主要思想是当出现字符串不匹配时,我们可以知道一部分之前已经匹配过的的文本内容,利用这些信息从而避免从头再开始匹配。
但是如何才能知道之前已经匹配过的内容呢?这是KMP算法的核心,也是KMP算法里面的next数组的用处。
3.最长相等前后缀
一个字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续字串
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
前缀表也就是next数组要求的是最长相等前后缀的长度,例如a的最长相等前后缀为0,aaa得到最长相等前后缀为2,aaba的最长相等前后缀为1。
4.next数组(前缀表)
KMP的核心就是next数组,当模板串和主串不匹配时,next数组是用来让模板串知道应该从哪里再开始匹配。
next数组记录下标i之前(包括i)的字符串中,有多大长度的相等前后缀。
这里借用了代码随想录的图片
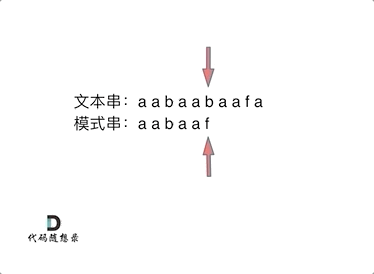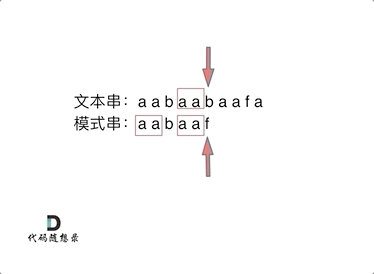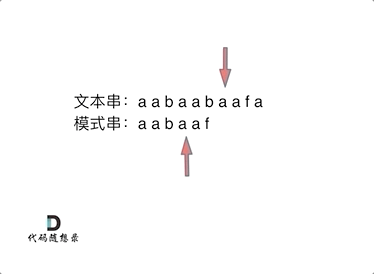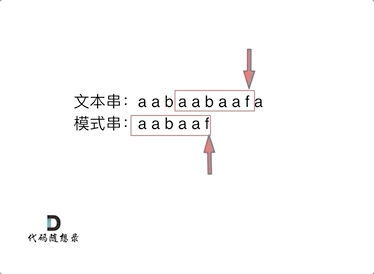
比如我们要在文本串aabaabaafa中寻找模板串aabaaf,在b和f之前发现匹配不了,如果用暴力算法,就要从头开始匹配,文本串和模板串都需要进行回退,时间复杂度是很高的,但如果我们使用KMP算法,next数组记录了f之前有多大长度的相等前后缀,也就是我们知道了之前匹配过的内容,就会从上次已经匹配的内容开始匹配,这里为什么能这样呢?我是这样理解的:
文本串: aabaabaafa 用i遍历
模板串:aabaaf 用j遍历
在b和f时不相同了,这时候我们不想再匹配我们已经匹配过的,也就是说我们不想i回退,而是一直向前走,那我们就要j进行回退,回退到什么位置呢,前面已经匹配到了,说明已经匹配过的文本串aabaa中含有模板串一部分内容,又因为前后缀有相等的部分。所以我们回退到前后缀相等的前缀位置,因为和文本串是相同的,所以aabaa的后缀aa和文本串的aabaa的后缀aa是相等的,又有aabaa的前缀aa和后缀aa是相等前后缀,所以前缀aa和文本串aabaa的后缀aa相等,我们回退到aabaa的b即可避免再次匹配aabaa的前缀aa,这样也可以保证模板串aabaa的前缀aa是已经匹配过的。
f之前这部分的字符串(也就是字符串aabaa)的最长相等前后缀是aa ,因为找到了最长相等的前后缀,匹配失败的位置是后缀的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。
5.如何计算next数组
例如a a b a a f
下标0 1 2 3 4 5
next 0 1 0 1 2 0当下标为0时,长度为前1个字符的字串a,最长相等前后缀的长度为0
当下标为1时,长度为前2个字符的字串aa,最长相等前后缀的长度为1
依次类比,可以得到next数组,也就是前缀表
可以看出模板串和next数组对应位置的数字表示的是下标i之前(包括i)的字符串中,有多大长度的最长相等前后缀。
当我们找到不匹配的位置时,就要看它前一个字符的next数组的值是多少,因为我们要找前面字符串的最长相等前后缀,所以要看前一位的next数组的值,前一个字符的next数组值为2,所以我们把下标j移动到2的位置继续匹配,这样就可以匹配到了。
6.next数组实现
主要是处理前后缀相等和不相等的情况,我们首先定义一个getNext函数来构造next数组,参数为指向next数组的指针,和一个字符串
void getNext(int* next,string& s)接着我们对其进行初始化,定义两个指针i和j,j指向前缀末尾,i指向后缀末尾,对next数组进行初始化赋值
int j=0;
next[0]=j;next[i]表示i(包括i)之前最长相等的前后缀长度,就是j,所以初始化next[0]=j
6.1前后缀不相同
j=0,所以我们从i=1开始,遍历文本串,就像这样
for(int i=0;ij首先要保证是大于0的,因为下面j要回退,然后就是s[i]和s[j]的比较,如果s[i]和s[j]不相同,j就要找前一位对应的回退位置,因为这里j之前的前缀已经和i的后缀不相等了,所以我们就要j进行回退。
while(j>=0&&s[i]!=s[j])
{
j=next[j-1];
}6.2前后缀相同
如果是s[i]和s[j]相同,这时候只要同时移动i和j,这时候找到了相同的前后缀,我们要把j的值赋值给next[i],因为next[i]记录相同前后缀的长度
if(s[i]==s[j])
{
j++;
}
next[i]=j;完整代码如下:
void getNext(int* next, const string& s)
{
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++)
{
while (j > 0 && s[i] != s[j])
{
j = next[j - 1];
}
if (s[i] == s[j])
{
j++;
}
next[i] = j;
}
}
7.例题 
void getNext(int* next,const string& s){
int j=0;
next[0]=0;
for(int i=1;i0&&s[i]!=s[j]){
j=next[j-1];
}
if(s[i]==s[j]){
j++;
}
next[i]=j;
}
}
int strStr(string haystack,string needle){
if(needle.size()==0){
return 0;
}
int next[needle.size()];
getNext(next,needle);
int j=0;
for(int i=0;i0&&haystack[i]!=needle[j]){
j=next[j-1];
}
if(haystack[i]==needle[j]){
j++;
}
if(j==needle.size()){
return (i-needle.size()+1) ;
}
}
return -1;
} 这道题很明显是字符串匹配的问题,所以我们使用KMP算法,首先是next数组的构建,这是模板,直接写就行,然后就是模板串和文本串的匹配,如果不相同,那j就回退到next[j-1],如果相同,j就直接向后移动即可,当j和模板串的长度相等时,此时i一定是大于等于模板串的长度的,因为i之前的文本串是包含模板串的,所以我们用i-模板串的长度+1就是第一个匹配项的下标了。