平衡二叉树详解 通俗易懂
平板就类似于一个世界,当诱惑降临的时刻,当人们心中的平衡被打破,世界就会变得混乱,最后留下的就是剩下孤独寂寞和失败。这种单调机械化的社会,经不起诱惑的侵蚀,很容易崩溃。最容易被侵蚀的,恰恰是最空虚的心灵,因此世界、社会的平衡对于秩序管理来说很重要。
我们接下来要详细的介绍与平衡有关的一种数据结构——平衡二叉树。
平衡二叉树是一种二叉排序树,其中每一个结点的左子树和右子树的高度差至多等于1。
有两位俄罗斯数学家早在1962年就共同发明一种解决平衡二叉树的算法,所以有不少资料中也称这样的平衡二叉树为AVL树
从平衡二叉树的名字,你也可以体会到,它是一种高度平衡的二叉树。那什么叫做高度平衡呢?
是一个好问题,意思就是说,要么它是一个空树,要么它的左子树和右子树都是平衡二叉树,且左子树与右子树的高度差的绝对值不能超过1.我们将二叉树上结点的左子树高度减去右子树高度的值称为平衡因子,平衡因子就是我们判断它有没有平衡的一个标志,当平衡因子的绝对值大于1时该树则不是平衡二叉树。
大家如果对于概念不太理解的话可以详细看看下面的几个二叉树,然后看看怎么去判断是不是平衡二叉树。
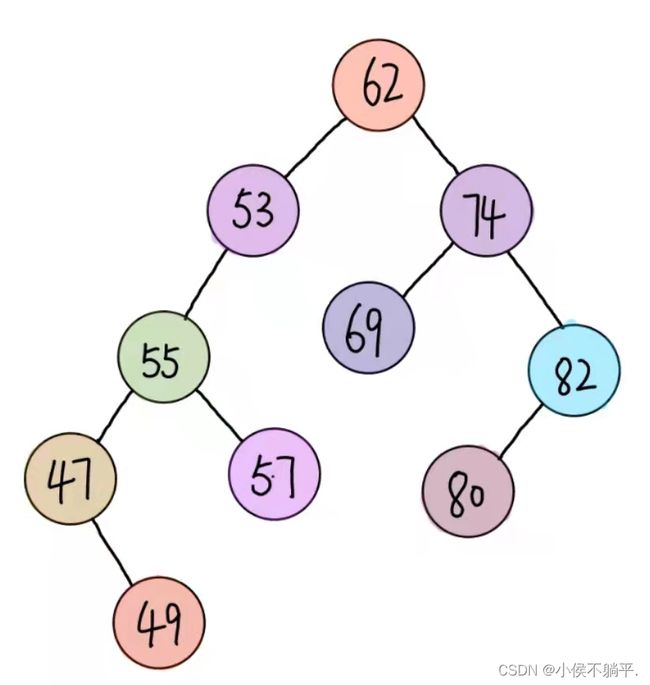
图1 平衡二叉树 图2 不是平衡二叉树
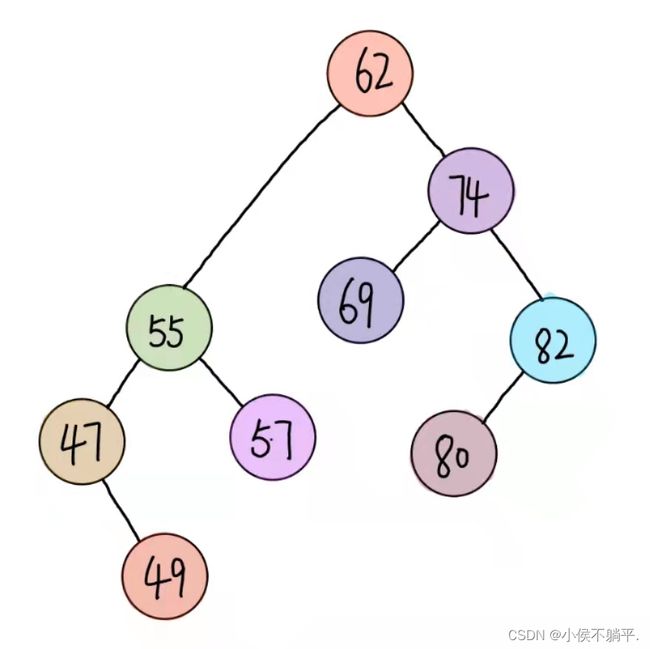
图3 不是平衡二叉树 图4 平衡二叉树
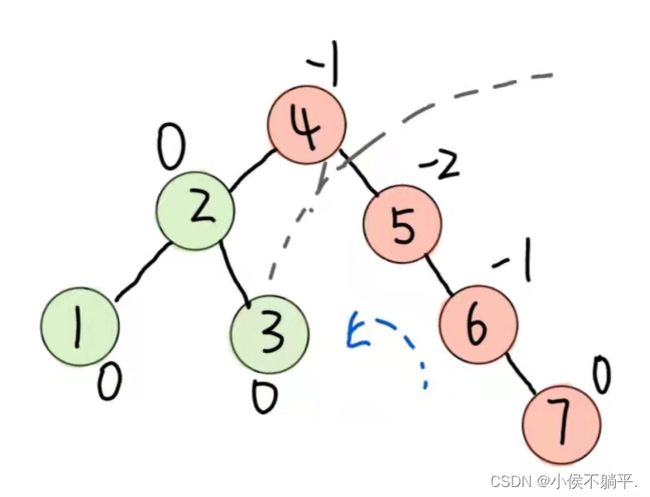
图一、图四的左子树和右子树都是相对于来说是平衡的。图2不是平衡二叉树的原因是它首先不是二叉排序树,结点55比结点53大但是还在53的左子树这样的二叉树不是二叉排序树。图3 是不满足平衡二叉树的原因是结点53的高度为3,而右子树为空,两者之差大于了绝对值1因此它不是平衡的。
距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,我们称为最小不平衡树,如下图所示:
平衡二叉树的实现原理
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中,每当插入一个结点的时候,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡树。在保持二叉排序树特性的前提下,调整最小不平衡树中各结点之间的连接关系,进行相应的旋转,使之称为新的平衡子树。
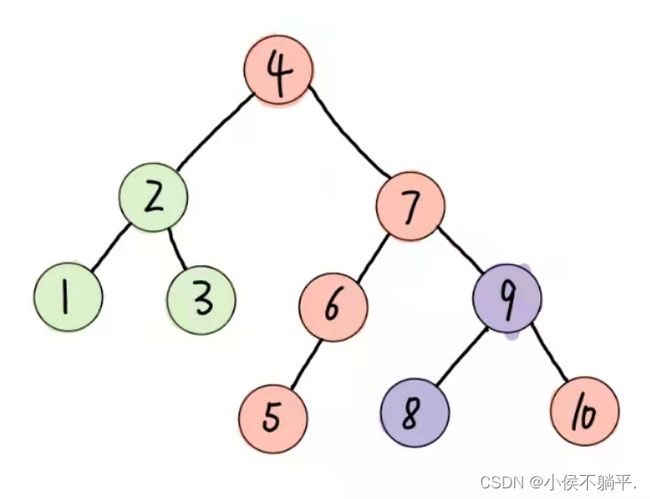
为了我们以后的讲解看起来更加轻松一点,我们先讲述一个平衡二叉树构建过程的例子。假设我们现在有一个数组a【10】={ 3,2,1,4,5,6,7,10,9,8}需要构建二叉排序树。在没有学习平衡二叉树之前,根据二叉排序树的特性,我们通常会将它构建称为图5的样子。虽然它完全符合二叉排序树的定义,但是对这样高度达到8的二叉树来说,查找是非常不利的。我们更期望它可以构建成图6的样子,高度为4的二叉排序树才可以提供高效的查找效率。那么我们现在就来研究如何讲一个数组构建成图6样子的二叉排序树。
图5 二叉排序树 图6 平衡二叉树
对于数组的前两位我们可以很正常的建立,到了第三个数字1时,发现此时的根结点3的平衡因子变为了2,此时整个树都成了最小不平衡树,因此需要作出相应的调整如下图1所示(左上角的数字为该结点的平衡因子BF的值)。因为BF值为正,因此我们对整个树进行右旋(顺时针旋转),此时结点2变成了根结点,3就成了2的右孩子,这样三个结点的平衡因子BF为都为0,非常平衡如下图2所示。
图 1 图 2
然后我们再增加结点4,平衡因子没有超出限定范围(-1,0,1),如图3.增加结点5时,结点3的BF值为-2,说明要进行旋转了,所以我们对这颗最小的不平衡子树进行左旋(逆时针旋转),如图4,此时整颗树又达到了平衡。
图 3
图 4 图 5
继续,增加结点6时,发现根结点2的BF值变成了-2,如下图6所示。所以我们对根结点进行了左旋操作,注意此时的本来结点3是4的左孩子,由于旋转后要满足二叉排序树的特性,因此它成了结点2的右孩子,如图7.增加结点7,同样的左旋,使得整棵树达到平衡,如图8,9所示。
图 6 图 7
图 8 图 9
当增加结点10时,结构无变化,如下图10所示。再增加结点9,此时结点7的BF值变成了-2,理论上我们只需要旋转最小不平衡子树7,8,9即可,但是如果左旋转后,结点9就变成了10的右孩子,这是不符合二叉排序树的特性,此时不能简单的进行左旋转如图11所示。我们发现根本原因在于结点7的BF为-2,而结点10的BF值为1,也就是说,它俩一正一负,符号不统一,而前面几次旋转符号都是统一的,全为负数则进行左旋转,全为正数则进行右旋转。遇到不统一的符号,我们先将其符号换成统一的再进行旋转,于是我们先对结点9,结点10进行右旋转,使得结点10称为结点9的右孩子,结点9的BF变为-1,此时就和结点7的符号相统一了,如图12所示。最后进行左旋转即可如下图13所示。
图 10 图 11
图 12 图 13
接着插入结点8,情况和刚刚的相似如图14所示,所以先进行右旋转,得到图15然后再对最小不平衡子树进行左旋转即可,得到图16。
图 14 图 15
图 16
以上就是对实例的详细介绍,大家可以多看看左旋转和右旋转的具体操作。
平衡二叉树的实现算法
首先是需要改进二叉排序树的结点结构,增加一个整型变量bf,用来存储平衡因子。
结构体的类型代码如下所示:
typedef struct BiTNode
{
int data;
int bf;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
右单旋转
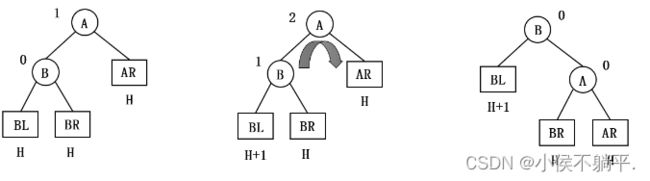
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致了以A为根的子树失去平衡。
需要一次向右的旋转操作:将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
如下图所示,结点旁的数值代表结点的平衡因子,方块表示相应结点的子树,方块下的数值代表该子树的高度,以下相同,不再赘述。
然后对于右旋转我们的代码如下:
void R_Rotate(BiTree *p) //右旋的操作
{
BiTree L;
L = (*p)->lchild;
(*p)->lchild = L->rchild;
L->rchild = (*p);
*p=L;
}此函数的代码的意思是说,当传入一个二叉排序树p,将它的左孩子定义为L,将L的右子树变成p的左子树,再将p改为L的右子树,最后将L替换p称为根结点。这样就完成了一次右旋转,如下图所示。
左单旋转
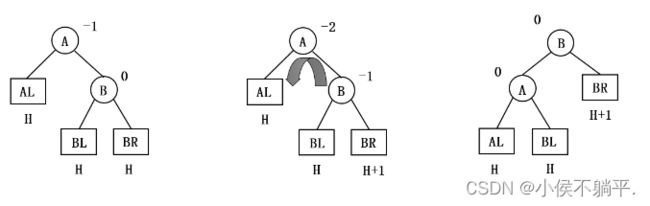
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡。
需要一次向左的旋转操作:将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树作为A结点的右子树。如下图所示:
实现代码:
void L_Rotate(BiTree *p) //左旋的操作
{
BiTree R;
R = (*p)->rchild;
(*p)->rchild = R->lchild;
R->lchild = (*p);
*p=R;
}先进行右旋转(将BF值符号变相同)再进行左旋转
由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡。
需要进行两次旋转操作:先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。如下图所示:
实现代码如下所示:
void LeftBlance(BiTree *T)
{
BiTree R,Rr;
R = (*T)->rchild;
switch(R->bf)
{
case 1:
(*T)->bf = R->bf = 0;
L_Rotate(T);
break;
case -1:
Rr = R->lchild;
switch(Rr->bf)
{
case -1:
(*T)->bf = 1;
R->bf = 0;
break;
case 0:
(*T)->bf = R->bf = 0;
break;
case 1:
(*T)->bf = 0;
R->bf = -1;
break;
}
Rr->bf = 0;
R_Rotate(&(*T)->rchild);
L_Rotate(T);
}
}先进行左旋转(将BF符号变相同)再进行右旋转
由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡。
需要进行两次旋转操作:先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置。如下图所示:
【注意】LR和RL旋转时,新结点究竟是插入C的左子树还是插入C的右子树均不影响旋转过程,在下面的图中以插入C的左子树中为例。
实现的代码如下:
void RightBlance(BiTree *T) //左平衡旋转处理
{
BiTree L,Lr;
L = (*T)->lchild;
switch(L->bf)
{
case 1:
(*T)->bf = L->bf = 0;
R_Rotate(T);
break;
case -1:
Lr = L->rchild;
switch(Lr->bf)
{
case 1:
(*T)->bf = -1;
L->bf = 0;
break;
case 0:
(*T)->bf = L->bf = 0;
break;
case -1:
(*T)->bf = 0;
L->bf = 1;
break;
}
Lr->bf = 0;
L_Rotate(&(*T)->lchild);
R_Rotate(T);
}
}平衡二叉树的插入算法AVL
平衡二叉树的插入过程前半部分与二叉排序树相同,但是在新结点插入后,若造成查找路径上的某个结点不再平衡,则需要做出相应的调整。
在新结点作为叶结点插入后,必须从插入位置沿到根结点的路径回溯,检查在此路径上的结点是否变得不平衡。若是,则找出其中的最小不平衡子树,在保持二叉查找树特性的情况下,调整最小不平衡子树中结点之间的关系,使之达到新的平衡;否则,本次插入结束。
所谓最小不平衡子树,是指插入后在所有失去平衡性的结点中,以离插入结点最近的结点作为根的那棵子树,这个根结点一定处于在查找插入位置时所经过的路径上。
然后,在找到的最小不平衡子树上识别平衡旋转类型(LL、RR、LR、RL),做完平衡旋转后,本次插入即可结束。
AVL的插入算法代码如下:
bool InsertAVL(BiTree *T,int e,bool taller)
{
if(!*T)
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data =e;
(*T)->lchild=(*T)->rchild=NULL;
(*T)->bf=0;
taller=false;
}
else
{
if(e==(*T)->data)
{
taller=false;
return false;
}
if(e<(*T)->data)
{
if(!InsertAVL(&(*T)->lchild,e,taller))
return false;
if(taller)
{
switch((*T)->bf)
{
case 1:
LeftBlance(T);
taller=false;
break;
case 0:
(*T)->bf=1;
taller=true;
break;
case -1:
(*T)->bf=0;
taller=false;
break;
}
}
}
else
{
if(!InsertAVL(&(*T)->rchild,e,taller))
return false;
if(taller)
{
switch((*T)->bf)
{
case 1:
(*T)->bf=0;
taller=false;
break;
case 0:
(*T)->bf=-1;
taller=true;
break;
case -1:
RightBlance(T);
taller=false;
break;
}
}
}
}
return true;
} 平衡二叉树的查找(具体详细介绍可以看往期博客二叉排序树)
该树的查找当时和删除的方式与二叉排序树一模一样的代码!只不过平衡二叉树的查找和删除操作对于二叉排序树来说更加快速,高效!
实现代码:
//查找的递归算法
BiTNode *Search(BiTNode *root, int x){
if(root->data == x){
return root;
}else if(x < root->data){
return Search(root->lchild, x);
}else{
return Search(root->rchild, x);
}
}平衡二叉树的删除
实现代码(具体详细介绍可以看往期博客二叉排序树):
//删除
bool Delete(BiTNode *p)
{
//在二叉排序树中删除结点p, 并重新连接它的左右子树
BiTNode *q, *s;
//1.p为叶子结点
if(p->lchild==NULL && p->rchild==NULL){
p = NULL;
}
//2.1 p左子树为空, 重接右子树
else if(p->lchild == NULL){
q = p;
p = p->rchild;
free(q);
}
//2.2 p右子树为空, 重接左子树
else if(p->rchild == NULL){
q = p;
p = p->lchild;
free(q);
}
//3. p左右子树均不为空
else{
q = p;
s = p->rchild; //找到p的右子树的最左端(中序直接后继)
while(s->lchild!= NULL){
q = s;
s = s->lchild;
}
p->data = s->data;
if(q != p) //判断是否执行上述while循环
q->lchild = s->rchild; //执行上述while循环,重接*q的左子树
else
q->rchild = s->rchild; //未执行上述while循环,重接*q的右子树,对于这个情况,可以参考代码后给出的示例图
free(s);
}
return true;
}
bool DeleteBST(BiTNode *root, int x)
{
if(root == NULL){
return false;
}else{
if(x == root->data)
return Delete(root);
else if(x < root->data)
return DeleteBST(root->lchild, x);
else
return DeleteBST(root->rchild, x);
}
}整体的实现代码如下所示:
#include
#include
typedef struct BiTNode
{
int data;
int bf;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void R_Rotate(BiTree *p) //右旋的操作
{
BiTree L;
L = (*p)->lchild;
(*p)->lchild = L->rchild;
L->rchild = (*p);
*p=L;
}
void L_Rotate(BiTree *p) //左旋的操作
{
BiTree R;
R = (*p)->rchild;
(*p)->rchild = R->lchild;
R->lchild = (*p);
*p=R;
}
void RightBlance(BiTree *T) //左平衡旋转处理
{
BiTree L,Lr;
L = (*T)->lchild;
switch(L->bf)
{
case 1:
(*T)->bf = L->bf = 0;
R_Rotate(T);
break;
case -1:
Lr = L->rchild;
switch(Lr->bf)
{
case 1:
(*T)->bf = -1;
L->bf = 0;
break;
case 0:
(*T)->bf = L->bf = 0;
break;
case -1:
(*T)->bf = 0;
L->bf = 1;
break;
}
Lr->bf = 0;
L_Rotate(&(*T)->lchild);
R_Rotate(T);
}
}
void LeftBlance(BiTree *T)
{
BiTree R,Rr;
R = (*T)->rchild;
switch(R->bf)
{
case 1:
(*T)->bf = R->bf = 0;
L_Rotate(T);
break;
case -1:
Rr = R->lchild;
switch(Rr->bf)
{
case -1:
(*T)->bf = 1;
R->bf = 0;
break;
case 0:
(*T)->bf = R->bf = 0;
break;
case 1:
(*T)->bf = 0;
R->bf = -1;
break;
}
Rr->bf = 0;
R_Rotate(&(*T)->rchild);
L_Rotate(T);
}
}
bool InsertAVL(BiTree *T,int e,bool taller)
{
if(!*T)
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data =e;
(*T)->lchild=(*T)->rchild=NULL;
(*T)->bf=0;
taller=false;
}
else
{
if(e==(*T)->data)
{
taller=false;
return false;
}
if(e<(*T)->data)
{
if(!InsertAVL(&(*T)->lchild,e,taller))
return false;
if(taller)
{
switch((*T)->bf)
{
case 1:
LeftBlance(T);
taller=false;
break;
case 0:
(*T)->bf=1;
taller=true;
break;
case -1:
(*T)->bf=0;
taller=false;
break;
}
}
}
else
{
if(!InsertAVL(&(*T)->rchild,e,taller))
return false;
if(taller)
{
switch((*T)->bf)
{
case 1:
(*T)->bf=0;
taller=false;
break;
case 0:
(*T)->bf=-1;
taller=true;
break;
case -1:
RightBlance(T);
taller=false;
break;
}
}
}
}
return true;
}
int preorder(BiTree T)
{
if(T==NULL)
return 0;
else
{
preorder(T->lchild);
printf("%d",T->data);
preorder(T->rchild);
return 0;
}
}
//查找的递归算法
BiTNode *Search(BiTNode *root, int x){
if(root->data == x){
return root;
}else if(x < root->data){
return Search(root->lchild, x);
}else{
return Search(root->rchild, x);
}
}
//删除
bool Delete(BiTNode *p)
{
//在二叉排序树中删除结点p, 并重新连接它的左右子树
BiTNode *q, *s;
//1.p为叶子结点
if(p->lchild==NULL && p->rchild==NULL){
p = NULL;
}
//2.1 p左子树为空, 重接右子树
else if(p->lchild == NULL){
q = p;
p = p->rchild;
free(q);
}
//2.2 p右子树为空, 重接左子树
else if(p->rchild == NULL){
q = p;
p = p->lchild;
free(q);
}
//3. p左右子树均不为空
else{
q = p;
s = p->rchild; //找到p的右子树的最左端(中序直接后继)
while(s->lchild!= NULL){
q = s;
s = s->lchild;
}
p->data = s->data;
if(q != p) //判断是否执行上述while循环
q->lchild = s->rchild; //执行上述while循环,重接*q的左子树
else
q->rchild = s->rchild; //未执行上述while循环,重接*q的右子树,对于这个情况,可以参考代码后给出的示例图
free(s);
}
return true;
}
bool DeleteBST(BiTNode *root, int x)
{
if(root == NULL){
return false;
}else{
if(x == root->data)
return Delete(root);
else if(x < root->data)
return DeleteBST(root->lchild, x);
else
return DeleteBST(root->rchild, x);
}
}
int main()
{
int i,x;
int a[10]={3,2,1,4,5,6,7,10,9,8};
BiTree T=NULL;
BiTNode *e;
e=(BiTNode *)malloc(sizeof(BiTNode));
bool taller;
for(i=0;i<10;i++)
{
InsertAVL(&T,a[i],taller);
}
preorder(T);
printf("\n请输入想要查找的数据->");
scanf("%d",&x);
e=Search(T,x);
printf("%d %d",e->data,e->bf);
printf("\n请输入想要删除的数据->");
scanf("%d",&x);
DeleteBST(T,x);
preorder(T);
return 0;
} 代码编译的时间相对于二叉排序树来说快了很多!!!
运行之后的结果如下图所示:
这篇博客的讲解就到此结束,下次更新博客应该就在放假之际了。在省运会比赛之际我应该也会根据实际情况进行相应的更新。