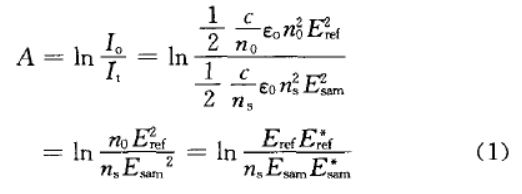朗伯比尔定律
1.概述
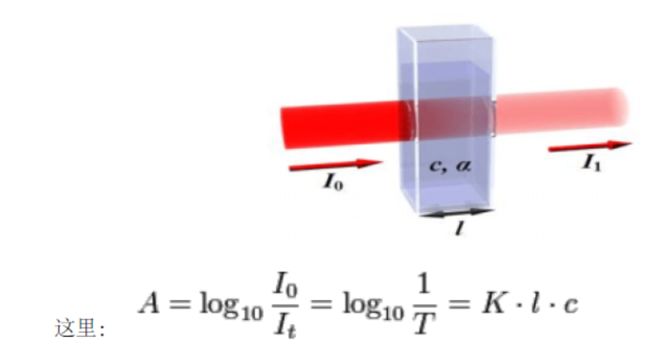
朗伯比尔定律(lambert-beer law)是分光光度法的基本定律,是描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系。[1]
2.物理性质
Io = 入射的单色光强度
I t = 透过光强度
l = 光程长度 (cm)
Τ 为透射比,或称透光度;
c = 吸光物质的浓度(mol/L 或g/L)
k= 吸光物质的吸收系数或摩尔吸收系数
Log I/Io 也称为吸光度![]()
3.使用前提条件
比尔- 朗伯定律的成立是有前提的,即:
1. 入射光为平行单色光且垂直照射;
2. 吸光物质为均匀非散射体系;
3. 吸光质点之间无相互作用;
4. 辐射与物质之间的作用仅限于光吸收过程,无荧光和光化学现象发生。根据比尔- 朗伯定律,当吸收介质厚度不变时, A 与c 之间应该成正比关系,但实际测定时,标准曲线常会出现偏离比尔- 朗伯定律的现象,有时向浓度轴弯曲(负偏离),有时向吸光度轴弯曲(正偏离)。造成偏离的原因是多方面的,其主要原因是测定时的实际情况不完全符合使比尔- 朗伯定律成立的前提条件。[3]
物理因素
1. 非单色光引起的偏离;
2. 非平行入射光引起的偏离;
3. 介质不均匀引起的偏离;
化学因素
1. 溶液浓度过高引起的偏离;
2. 化学反应(如水解、解离)引起的偏离;
4.表达形式
在红外分析中可以直接测得光的强度,而太赫兹波段测量的物理量是电场强度。。因此,在太赫兹检测中的吸光度如式(1):
其中n0=1,第一个等式为红外中吸光度的表达,推导的最终等式为太赫兹波段吸光度表达式。朗伯比尔定律应用于定量分析时的应用表达如式(2):[4]
基于传统的太赫兹检测技术中的模型计算得到的吸收系数表达式如式(3):
5.定律应用分析
红外光谱分析中,物质在一定波长处的吸光度与它的浓度呈线性关系。通过测定溶液对一定波长入射光的吸光度,可求得溶液中物质浓度和含量,通常选择最大波长处的吸光度进行分析,[5]这样可以得到最大的灵敏度。选用对太赫兹波具有敏感吸收的谷氨酰胺Glutamine(Gin)进行单一组分在不同浓度时的吸收测试,实验装置与文献一致。这里的单一组分并不是只有一种物质,而是一种吸收物质与稀释剂PE(在太赫兹波段基本无吸收)的混合,PE的添加保证了能够探测到物质与太赫兹波作用后的信息。按照Gin浓度由小到大进行样片的设计,详细信息见表1。Glnl与其他两个样片的浓度比例关系为:1:2.346和1:3.902。通过对比不同比例样片的太赫兹吸收谱,找出太赫兹波的吸收与物质浓度之间的关系。
分别从吸光度和吸收系数这两个角度表征单一组分中朗伯比尔定律的应用,即物质对太赫兹波吸收多少与其浓度的关系。
5.1不同浓度样片的吸光度
观察图2中三条谱线,样片Glnl,Gln2和Gln3的吸光度分别对应于虚线,点线和实线。从吸光度轴的数值上可以看出,随着浓度的增加,吸光度值在1.5 THz之后的频段内有增大的趋势。Glnl和Gln2的谱线形状基本相同,这说明可以用太赫兹谱进行Gin的定性分析;吸收幅值发生变化,表明可以进行Gin的定量分析。
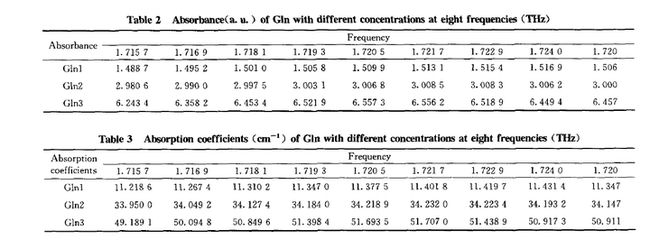
但是当物质浓度大于1tool·L 后,高频段的峰突然出现下降的小峰,不同于两个低浓度的样片吸收情况。这说明当物质的浓度比较大时对太赫兹波的吸收不能简单的只考虑浓度这一因素的影响,也从实验上证明了朗伯比尔定律不适用于高浓度的定量分析。物质对太赫兹波的敏感吸收体现在特征吸收峰处,Gin的特征吸收在1.72 THz附近,为了避免因选取一个点而引入的绝对误差,采取1.72 THz周围的8个数据点进行分析。表2记录了三组不同浓度谷氨酰胺在1.72 THz周围的吸光度值,最后一列是对这八个频率点和对应的吸光度计算的平均值,目的是找出吸光度和浓度之间的关系,将平均值列出图表示,见图3。
图3中虚线为拟合的浓度与吸光度的关系,三个星点为实测的吸光度值。整体观察可以认为吸光度数据与浓度满足近似线性关系。利用拟合优度的R2指标作为评价吸收与浓度二者线性度的指标,R2的计算式为:
利用表2中最后一列数据计算得到吸光度与浓度关系的R2指标值为0.966 8。
5.2不同浓度样片的吸收系数
使用与计算吸光度相同的时域脉冲数据,利用式(3)进行吸收系数谱的计算,结果见图4。只是在0.3~1.5 THz前Gln2的吸收多于Gln3的吸收,但是在特征峰处,随着浓度的增加,吸收系数在有效频段内基本满足随浓度增大而增大的趋势。
同样选取1.72 THz附近的8个频率点的吸收系数值进行分析,见表3。平均值列是对这八个频率点和对应的吸收系数值计算的平均值,目的是找出吸收系数和浓度之间的关系,见图5的平均值列各数据图。
图5中的1.72 THz处的吸收系数与浓度的关系,与图3的不同。按照式(4)计算的R 指标值为0.983 3,大于浓度与吸光度的拟合优度。
5.3吸光度与吸收系数的对比
吸光度谱和吸收系数谱的计算使用相同的时域脉冲信号,均采用傅里叶变换获得电场的幅值和相位,保证THz的1.724 0 THz,对比分析表2和表3中数据,表明当将朗伯比7~1.724 0 THz,对比分析表2和表3中数据,表明当将朗伯比尔定律应用于太赫兹波段的分析时不能只是简单的移植,要考虑到太赫兹波段与红外波段测试方法不同,引起测试样品的厚度不能保证完全相同,利用拟合优度的R 指标评价物质吸收与浓度的线性关系,可以看到吸收系数的R 大于吸光度R2值,表明吸收系数与浓度的线性关系较好,应选用吸收系数进行单一组分的浓度分析较合适。
6.分光光度法
分光光度法是利用物质所特有的吸收光谱来鉴别物质或测定其含量的一项技术,此技术灵敏、精确、快速和简便,为生物化学研究中广泛使用的方法。
(一)分光光度法的基本原理
基本原理是朗伯-比尔定律(Lambert-Beer’sLaw),又称吸收定律,即当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度(absorbance,A)与吸光物质的浓度(consenreation,C)及吸收层厚度(length,L)成正比, 用公式表示为:A = ε C L其中A为光度,ε为摩尔吸光系数,C为吸光物质浓度,L为吸光溶液的厚度。
光波是指波长在0.3~3 μm之间的电磁波(图1-1),颜色跟波长和频率有关,分为可见光和不可见光(表1-1)。可见光指能引起视觉的电磁波,波长在400-700 nm,其中紫光频率最大,波长最短,红光恰好相反。不可见光主要包括红外线、紫外线、伦琴射线。发射光的物体叫做光源,光源分为自然光和人造光。按照发光原理分为辐射发光、电子发光、化学发光、生物发光等。
(二)分光光度法的应用
1.定量分析 待测样品浓度的测定在实际工作中,由于盛放溶液的比色杯厚度是一致的,待测物质的浓度可通过以下几种方法测得:
(1)标准比较法(standard comparative method):在相同条件下,配制标准溶液和待测样品溶液,测定它们的吸光度。比较两者的吸光度,即可求出待测样品溶液的浓度。
(2)标准曲线法(standard curve method):配制一系列浓度由小到大的标准溶液,测出其吸光度。以各标准溶液的浓度为横坐标,相应的吸光度为纵坐标,在方格坐标纸上绘出标准曲线。在相同条件下测出待测样品的吸光度后,从标准曲线上可以直接查出其浓度。此法通常适用于大批样品的分析。
(3)标准系数法(standard coefficient method):多次测定标准液的吸光度后,按下式求出标准系数。
标准系数 = 标准液浓度/标准液平均吸光度也可从标准曲线上求出标准系数,再用同样方法测定待测溶液的吸光度,并代入下式求出待测物质的浓度。
(三)分光光度法的误差
1.溶液浓度待测物质溶液的浓度过高或过低都会偏离郎伯-比尔定律,影响检测的准确度。一般情况下,待测物质溶液浓度的吸光度在0.1~0.8之间最符合光吸收定律,此时检测线性好,读数误差小。如吸光度不在此范围,可适当稀释或浓缩比色溶液再进行测定。
2.干扰物质某些物质能干扰待测物质显色反应过程,或其本身具有与待测物质相同或相似的光吸收特性。这些物质存在于待测溶液中时,会使溶液测定值与待测物质实际浓度不相符合,因而产生误差。
3.反射光与散射光待测溶液与参比溶液的光折射率不同时,会引起发射损失的不同。待测溶液浑浊,入射光通过时会产生散射效应。这些非吸收作用都会产生测量误差。
4.仪器噪声分光光度计的噪声主要由光源强度、电子器件和光电管所产生的。仪器噪声过大,可严重影响测定的灵敏度和准确度。[6]
5.吸收池吸收池的不匹配、透光面不平行或定位不准确等,都会使其透光率产生差异,使测定结果产生误差。