【数据结构】三、栈
目录
一、栈
练习
二、栈实现-顺序栈
三、栈实现-链栈
练习
1.十进制转二进制(递归+非递归)
2.括号匹配
3.中缀转后缀+计算表达式
4.汉诺塔
栈和队列是限定插入和删除只能在表的“端点”进行的线性表
一、栈
特性:
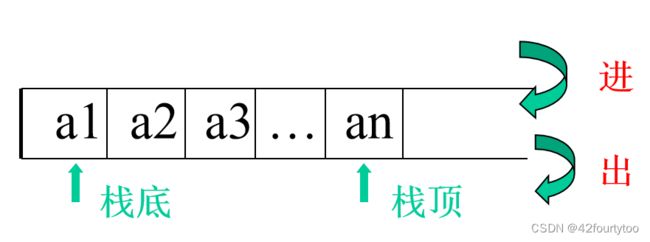
栈是限制仅在表尾进行插入和删除的特殊线性表,表尾称为栈顶,另一端为栈底
栈后进先出
用途:
调用函数或子程序时会采用栈结构,遵循“后进先出”的原则
递归过程采用栈结构,先向后递归,再依次向前返回
练习
六个元素按1,2,3,4,5,6 的顺序进栈,问下列哪一个不是合法的出栈序列?A
- A. 5 4 3 6 1 2
- B. 4 5 3 2 1 6
- C. 3 4 6 5 2 1
- D. 2 3 4 1 5 6
答案:A(不可能先1后2)
设栈的初始状态为空,元素1、2、3、4、5、6依次入栈,得到的出栈序列是(2, 3, 6, 5, 4, 1),则栈的容量至少是( )。注:栈指针指向堆栈最后一个元素
- A. 6
- B. 2
- C. 3
- D. 4
答案:D
二、栈实现-顺序栈
操作:
| 初始化栈(initstack) | 分配空间,初始化栈顶、栈底指针 |
| 压栈(push) | 插入元素为新的栈顶元素 |
| 出栈(pop) | 删除栈顶元素,并用 e 返回其值 |
| 获取栈顶元素(gettop) | 用 e 返回 S 的栈顶元素 |
| 显示栈内元素(show) | 由栈底到栈顶依次输出 |
代码:
#include
#include
#define SIZE 50
#define elemtype int
typedef struct stack {
elemtype* elem;
int top;
int base;
}stack;
void initstack(stack& s)
{
s.elem = (elemtype*)malloc(sizeof(elemtype) * SIZE);
if (!s.elem) return;
s.top = s.base = 0;
}
void push(stack& s, int value)
{
if (s.top == SIZE) return;
s.elem[s.top++] = value; //先压,(指针)后加
}
elemtype pop(stack& s, elemtype& e)
{
if (s.base == s.top) return NULL;
e = s.elem[--s.top]; //先减,后弹
return e;
}
elemtype gettop(stack& s, elemtype& e) //获取栈顶
{
if (s.base == s.top) return NULL;
e = s.elem[s.top - 1];
return e;
}
void show(stack s)
{
for (int i=0;i 三、栈实现-链栈
代码:
#include
#include
//节点类型
typedef struct node {
int data;
struct node* next;
}node, *pnode; //用typedef才能给结构体重新命名
//栈类型
typedef struct stack {
node* stacktop; //始终指向栈顶结点
int size;
}stack;
stack* initstack() //初始化栈
{
stack* newstack = (stack*)malloc(sizeof(stack));
if (newstack == NULL) {
printf("fail");
return NULL;
}
newstack->size = 0;
newstack->stacktop = NULL;
return newstack;
}
pnode createnode(int value) //生成新节点
{
node* newdata = (node*)malloc(sizeof(node)); //sizeof里面是node,不是node*,不然内存分配不够
if (newdata == NULL) {
printf("fail");
return NULL;
}
newdata->data = value;
newdata->next = NULL;
return newdata;
}
void push(stack* mystack, int value) //入栈
{
node* newnode = createnode(value);
newnode->next = mystack->stacktop; //头插法
mystack->stacktop = newnode;
mystack->size++;
}
void gettop(stack* mystack, int& e) //获取栈顶数据,用e返回
{
if (mystack->size == 0) {
printf("stack is empty");
return;
}
e = mystack->stacktop->data;
}
void pop(stack* mystack) //出栈
{
if (mystack->size == 0) {
printf("stack is empty");
}
else {
pnode oldtop = mystack->stacktop;
pnode newtop = mystack->stacktop->next;
mystack->stacktop = newtop;
free(oldtop);
mystack->size--;
}
}
void showstack(stack* mystack) //从栈顶到栈底显示栈内数据
{
for (pnode temp = mystack->stacktop; temp; temp = temp->next)
printf("%d ", temp->data);
printf("\n");
}
int main() {
stack* stack1 = initstack();
push(stack1, 1);
push(stack1, 2);
push(stack1, 4);
showstack(stack1);
int top;
gettop(stack1, top);
printf("%d\n", top);
push(stack1, 4);
showstack(stack1);
} 练习
1.十进制转二进制(递归+非递归)
思路:将十进制数不断除以2,直到数变为0停止。将余数倒序输出
//十进制转二进制函数,用链栈实现
void non_recursiveD2B(int num) //非递归
{
stack* s1 = initstack();
while (num != 0)
{
int n = num % 2;
push(s1, n);
num = num / 2;
}
showstack(s1);
}
void recursiveD2B(int num) //递归
{
if (num == 0)
return;
recursiveD2B(num / 2);
printf("%d", num % 2);
}
2.括号匹配
编写一个函数,判别一个表达式的括号是否正确匹配
思路:
- 出现左括弧,则进栈
- 出现右括弧,检查栈是否空:若栈空,则表明该“右括弧”多余;栈不空,和栈顶元素比较
- 右括弧和栈顶元素相比:若相匹配,则“左括弧出栈” ;否则,该表达式不匹配
- 表达式检验结束时:若栈空,且状态为1,则表明表达式匹配;否则不匹配。
void correct(stack*& s) //括号匹配函数,用链栈实现
{
printf("输入字符串:");
int state = 1; //表明状态,1为匹配,0不匹配
char temp = getchar();
while (temp!='\n' && state)
{
switch (temp) //只对括号类字符做操作;左括号-入栈,右括号-看栈顶是否为相匹配的左括号
{
case '(': {
push(s, temp);
break;
}
case ')': {
if (s->size != 0 && gettop(s) == '(')
pop(s);
else state = 0;
break;
}
case '[': {
push(s, temp);
break;
}
case ']': {
if (s->size != 0 && gettop(s) == '[')
pop(s);
else state = 0;
break;
}
case '{': {
push(s, temp);
break;
}
case '}': {
if (s->size != 0 && gettop(s) == '{')
pop(s);
else state = 0;
break;
}
}
temp = getchar();
}
if (s->size == 0 && state) //栈空且状态为1则匹配
printf("匹配");
else
printf("不匹配");
}
3.中缀转后缀+计算表达式
输入一个算术表达式,将它转为后缀表达式,再计算其结果。算术表达式包括以下运算符: ( ) + - * / 采用堆栈实现。(简化,参与运算的数字为个位正整数)
中缀转后缀遵循以下规则:
需要一个后缀栈suffix_stack,一个符号栈char_stack;从左至右依次遍历中缀表达式各个字符
- 字符为 数字 : 直接进入后缀栈
- 字符为 左括号 :入符号栈
- 字符为 右括号 :将符号栈持续出栈,出栈字符依次送入后缀栈,直到遇到左括号停止(左括号也要出栈,但不送入后缀栈)。
- 字符为 操作符 :判断该字符与符号栈栈顶的优先级,若字符>栈顶,字符入符号栈;否则将符号栈全部出栈,放入后缀栈,该字符再入符号栈。
- 将算术表达式遍历完后,把符号栈剩余元素转移至字符栈
优先级:简单来说,加减小于乘除。
比如,此时要把符号栈元素都转移到后缀栈,再把+或-放入符号栈;
反之,读入字符为*或/,符号栈栈顶为+或-,直接放入符号栈。
代码:中缀转后缀是函数infix_to_suffix,计算是calc
计算表达式的规则:
从栈底开始遍历后缀栈,数字放入结果栈;遇到符号从结果栈取出最后两位进行运算,结果放入结果栈。
//算术表达式的求值。算术表达式包括以下运算符: ( ) + - * / 。采用顺序栈实现。只能是个位数。
#include
#include
#define SIZE 50
typedef struct stack {
char* elem;
int top;
int base;
}stack;
void initstack(stack& s) {
s.elem = (char*)malloc(SIZE);
if (!s.elem) return;
s.top = s.base = 0;
}
void push(stack& s, char value) {
if (s.top == SIZE) return;
s.elem[s.top++] = value;
}
char pop(stack& s) {
if (s.base == s.top) return NULL;
return s.elem[--s.top];
}
char gettop(stack& s) {
if (s.base == s.top) return NULL;
return s.elem[s.top - 1];
}
void show(stack s) {
for (int i=0;i 注:还有一种不得出后缀式,直接得结果的方法。区别在于,当运算符从符号栈到对象栈时,就要将末尾两个数字进行计算。
表达式3* 2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和算符栈为( ),其中^为乘幂 。
- A. 3,2,4,1,1; *^(+*-
- B. 3,2,8; *^-
- C. 3,2,4,2,2; *^(-
- D. 3,2,8; *^(-
答案:D 减号优先级小于乘号,运算符出栈至左括号,减号再进栈
4.汉诺塔
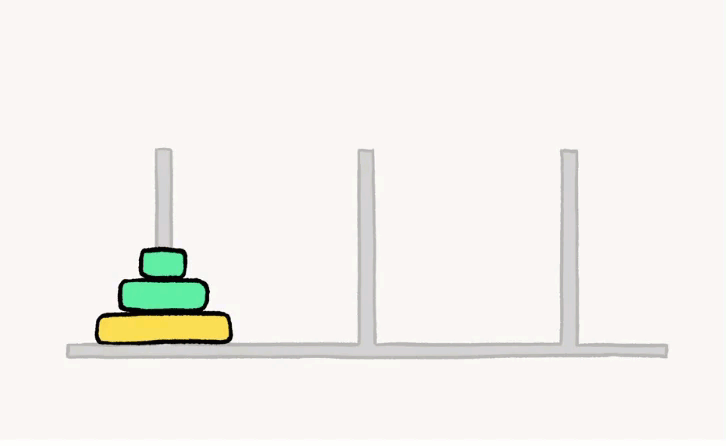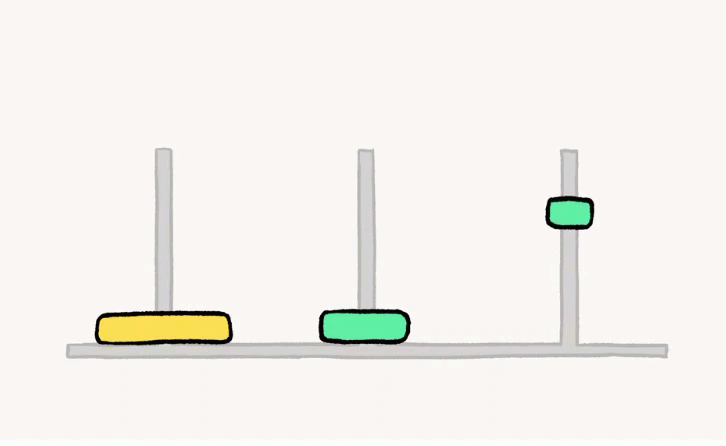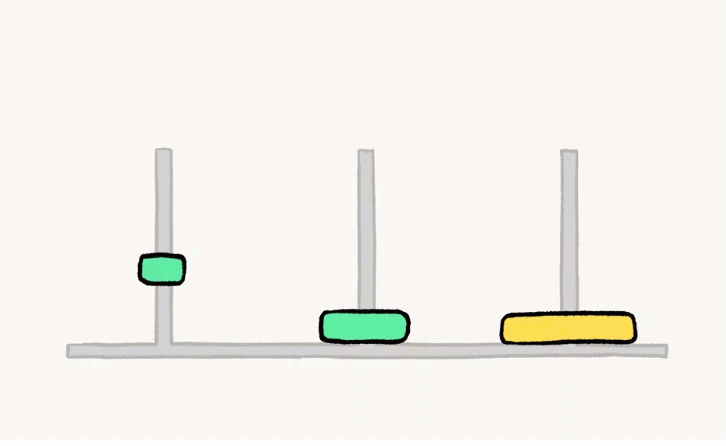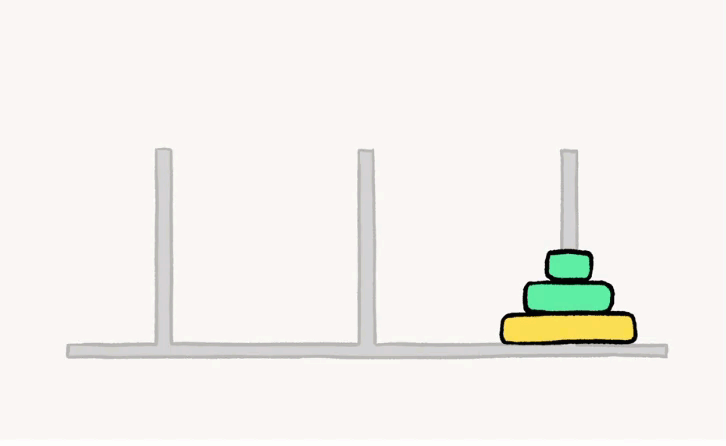
现有三个柱子A、B、C,其中有n个圆盘在A柱上,按照上小下大的规律放置。目标:把这n个圆盘从A柱借助B柱移动到C柱上,仍按照上小下大放置。
思路:递归思想
假如只有两个方块,假设上面是1号,下面是二号:
- 将1号从 起始柱 移到 中转柱
- 将2号从 起始柱 移到 目标柱
- 将1号从 中转柱 移到 目标柱
假如有n个方块,我们只需要:
- 将上面n-1个方块从 起始柱 移到 中转柱
- 将最下面的n号方块从 起始柱 移到 目标柱
- 将n-1个方块从 中转柱 移到 目标柱
然而 ,n-1个方块的移动同样是汉诺塔算法。他们只是三个柱子的作用变了。
//hanoi
#include
#include
void hanoi(int num, char x, char y, char z) //对整个问题来说,x是起始,y是中转,z是目标
{
if (num == 0)return; //递归算法通常以判断返回开头。num为0时不成立,返回即可
hanoi(num - 1, x, z, y); //将n-1个方块进行汉诺塔,注意传参的变化,对n-1来说,x是起始,z是中转,y是目标
printf("%d from %c to %c\n", num, x, z); //将n号块移到目标柱
hanoi(num - 1, y, x, z); //将n-1个方块进行汉诺塔,此时n-1来说,y是起始,x是中转,z是目标
}
int main()
{
int num;
printf("how many?");
scanf_s("%d", &num);
hanoi(num, 'x', 'y', 'z');
}