机器学习(23) SVM 示例4:【Python】解决二分类(示例1、2、3)

1 sklearn.svm.svc详解

1. Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。里面包含了SVM的程序，直接调用调节参数即可。
2. svm.SVC( ) 可以选择C值，以及核函数，调用之后先fit，再predict，predict时输入为一个二维数组，因此在画等高线的时候需要先把网格展开成二维数组进行predict再重新组成网格画图。在选择核函数时可以自己定义，例如：svm.SVC(kernel=my_kernel)，内置核函数默认为rbf高斯核,其中包含一个gamma关键词，gamma默认为1/n_features。

函数原型

sklearn.svm.SVC(

C=1.0,            # SVC的惩罚参数，float; 默认值是1.0

                      #    一般取值为10的n次幂，

                      #    如10的-5次幂,10的-4次幂…,10的0次幂,10,1000,10000

                      #    在python中可以使用pow(10,n) n=-5~inf

                      #    C越大,相当于希望松弛变量接近0,即对误分类的惩罚增大,

#       趋向于对训练集全分对的情况，这样会出现训练集测试时准确率

#       很高，但泛化能力弱。

                      #    C值小，对误分类的惩罚减小，容错能力增强，泛化能力较强。

    kernel='rbf',     # 核函数，str; 默认是'rbf', 可以是:

                      #   'linear',       0  – 线性：u'v

                      #   'poly',         1 – 多项式：(gamma*u'*v + coef0)^degree

                      #   'rbf',          2 – RBF函数：exp(-gamma|u-v|^2)

                      #   'sigmoid',      3 –sigmoid：tanh(gamma*u'*v + coef0)

                      #   'precomputed',  4 -核矩阵，该矩阵表示自己事先计算好的，

                      #                        输入后算法内部将使用提供的矩阵进行计算

                      #   自己指定，自定义的核函数名 degree=3,        

                      # 多项式poly函数的维度，int; 默认是3，选择其他核函数时会被忽略。

     gamma='auto',     # 'rbf','poly' 和'sigmoid'的核函数参数,float;

                                 #       默认是'auto'，则会选择1/n_features

    coef0=0.0,        # 核函数的常数项,float;对于'poly'和 'sigmoid'有用。

    shrinking=True,   # 是否采用shrinking heuristic方法，bool; 默认为true

    probability=False,# 是否采用概率估计,bool; 默认为False

    tol=0.001,        # 停止训练的误差值大小，float; 默认为1e-3

    cache_size=200,   # 指定训练所需要的内存大小，以MB为单位，float; 默认为200

    class_weight=None,# 类别的权重，字典类型或者, 'balance'字符串。默认为None

                      #    给每个类别分别设置不同的惩罚参数C，则该类别的惩罚系数为class_weight[i]*C

                      #    如果没有给，则会给所有类别都给C=1，即前面参数指出的参数C。

                      #    如果给定参数'balance',则使用y的值自动调整与输入数据中的类频率成反比的权重

verbose=False,    # 是否启用详细输出, bool; 默认为False。

                        # 此设置利用libsvm中的每个进程运行时设置，如果启用，

# 可能无法在多线程上下文中正常工作。

    max_iter=-1,      # 最大迭代次数,int; 默认位-1，-1表示为无限制。

    decision_function_shape=None, # 'ovo', 'ovr' or None, 默认为None

    random_state=None # 在混洗数据时所使用的伪随机数发生器的种子，默认为None

                       #     如果选int，则为随机数生成器种子；

                       #     如果选RandomState instance，则为随机数生成器；

                       #     如果选None,则随机数生成器使用的是np.random

    )

其中，主要调节的参数：C、kernel、degree、gamma、coef0。

SVC的函数

函数	作用
svc.fit(X, y[, sample_weight])	根据给定的训练数据拟合SVM模型。 只需要给出数据集X和X对应的标签y即可。
svc.predict(X)	根据测试数据集进行预测 基于以上的训练，对预测样本X进行类别预测，因此只需要接收一个测试集X，该函数返回一个数组表示个测试样本的类别。
svc.predict_log_proba(X_test) svc.predict_proba(X_test)	当sklearn.svm.SVC(probability=True)时，才会有这两个值，分别得到样本的对数概率以及普通概率。 这与predict方法不同，predict方法返回的输入样本属于那个类别，但没有概率。使用此两个方法时，需要在初始化时，将 probability参数设置为True。
svc.score(X, y[, sample_weight])	返回给定测试数据和标签的平均精确度
svc.get_params([deep])	获取此估算器的参数并以字典行书储存,默认deep=True，
svc.decision_function(X)	返回样本X到分离超平面的距离

SVC的属性

属性	含义
svc.coef_[0]	权重
svc.intercept_	bias，偏差
svc.n_support_	各类各有多少个支持向量
svc.support_	各类的支持向量在训练样本中的索引
svc.support_vectors_	各类所有的支持向量

 应用示例

import numpy as np

import matplotlib.pyplot as plt

from sklearn import svm

# 1 、创建40个独立的点

np.random.seed(0)

X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]

y = [0] * 20 + [1] * 20

# 2 、可视化数据

# 2.1 定义可视化数据函数

def plot_data(x,y):

    n = x[y == 0]

    p = x[y == 1]

    plt.scatter(p[:,0],p[:,1],c='r', marker='x', label='y=1')

    plt.scatter(n[:,0],n[:,1],c='g', marker='o', edgecolors='g', linewidths=0.5, label='y=0')

    plt.legend(loc ='upper right')

    plt.show

# 2.2 定义绘制决策边界函数

def plot_boundary(svc,x,colors):

    u = np.linspace(np.min(x[:,0]),np.max(x[:,0]),500)

    v = np.linspace(np.min(x[:,1]),np.max(x[:,1]),500)

    x,y = np.meshgrid(u,v)#将x,y转化为网格（500*500）

    z = svc.predict(np.c_[x.flatten(),y.flatten()])#因为predict中是要输入一个二维的数据，因此需要展开

    z = z.reshape(x.shape) #重新转为网格

    plt.contour(x,y,z,1,colors = colors) #画等高线

    plt.title('The Decision Boundary')

    plt.show

# 2.3 可视化数据

plot_data(X,y)

# 3 、选择模型

svc1  = svm.SVC(C= 1.0,kernel='linear',probability=True)

# 4 、 按模型训练

svc1.fit(X, y)

# 5、绘制决策边界

plot_boundary(svc1,X,'b')

# 5 、打印各种函数结果

print(f'预测样本数据X的标签 svc.predict(X) ={svc1.predict(X)}')

print(f'预测样本数据X的对数概率 svc.predict_log_proba(X) ={svc1.predict_log_proba(X)}')

print(f'预测样本数据X的普通概率svc.predict_proba(X) ={svc1.predict_proba(X)}')

print(f'预测样本数据X和标签y的平均精确度 svc.score(X,y) ={svc1.score(X,y)*100}%')

print(f'模型参数 svc.get_params() ={svc1.get_params()}')

print(f'样本X到分离超平面的距离 svc.decision_function(X) ={svc1.decision_function(X)}')

2 【python代码】解决线性、非线性（决策边界清晰/模糊）二分类

## Part1 导入数据

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
 
data1 = loadmat('ex6data1.mat')
data2 = loadmat('ex6data2.mat')
data3 = loadmat('ex6data3.mat')
 
print(f'数据集ex6data1中的键名 = {data1.keys()} ')
print(f'数据集ex6data2中的键名 = {data2.keys()} ')
print(f'数据集ex6data3中的键名 = {data3.keys()} ')

# 1.1 数据处理
X1,y1 = data1['X'],data1['y'].flatten()
X2,y2 = data2['X'],data2['y'].flatten()
X3,y3 = data3['X'],data3['y'].flatten()
Xval,yval = data3['Xval'],data3['yval'].flatten()
X1.shape,y1.shape#((51, 2), (51,))
X2.shape,y2.shape#((863, 2), (863,))
X3.shape,y3.shape#((211, 2), (211,))
Xval.shape,yval.shape#((200, 2), (200,))

# 1.2 定义可视化数据函数
def plot_data(x,y):
    n = x[y == 0]
    p = x[y == 1]
    plt.scatter(p[:,0],p[:,1],c='r', marker='x', label='y=1')
    plt.scatter(n[:,0],n[:,1],c='g', marker='o', edgecolors='g', linewidths=0.5, label='y=0')
    plt.legend(loc ='upper right')
    plt.show

# 1.3 定义绘制决策边界函数
def plot_boundary(svc,x,colors):
    u = np.linspace(np.min(x[:,0]),np.max(x[:,0]),500)
    v = np.linspace(np.min(x[:,1]),np.max(x[:,1]),500)
    x,y = np.meshgrid(u,v)#将x,y转化为网格（500*500）
    z = svc.predict(np.c_[x.flatten(),y.flatten()])#因为predict中是要输入一个二维的数据，因此需要展开
    z = z.reshape(x.shape) #重新转为网格
    plt.contour(x,y,z,1,colors = colors) #画等高线
    plt.title('The Decision Boundary')
    plt.show

# 1.4 定义高斯函数 ——用于线性不可分（决策边界清晰）
def gaussianKernel(x1,x2,sigma):
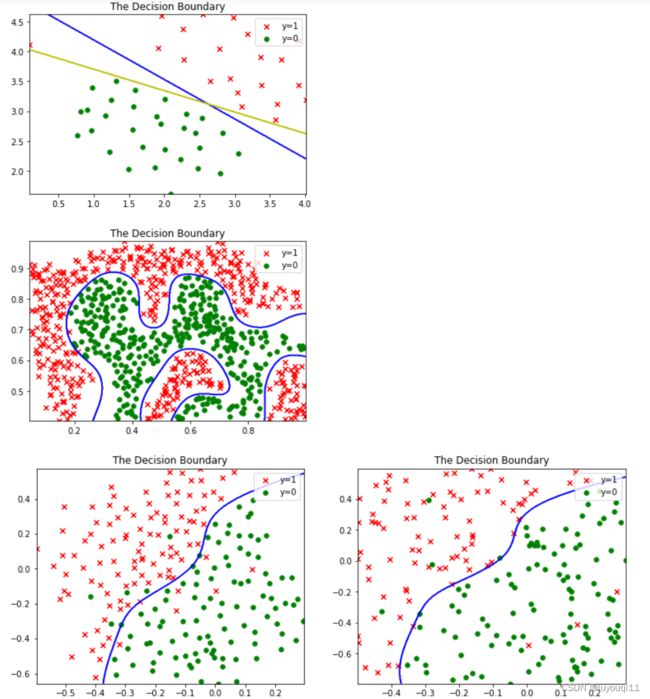
    return np.exp( -((x1-x2).T@(x1-x2)) / (2*sigma*sigma) )

## part2 线性可分SVM

# 2.1 可视化样本
plt.figure(1)
plot_data(X1,y1)

# 2.2 用sklearn拟合并预测
#   Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，
#   包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。
#   里面包含了SVM的程序，直接调用调节参数即可。
#   svm.SVC( ) 可以选择C值，以及核函数，调用之后先fit，再predict，predict时输入为一个二维数组，
#   因此在画等高线的时候需要先把网格展开成二维数组进行predict再重新组成网格画图。
#   在选择核函数时可以自己定义，例如：svm.SVC(kernel=my_kernel)，内置核函数默认为rbf高斯核,
#   其中包含一个gamma关键词，gamma默认为1/n_features。

from sklearn.svm import SVC

# 2.2.1 误差项惩罚系数C=1
svc1 = SVC(C = 1,kernel = 'linear')#线性核函数
svc1.fit(X1,y1.flatten())
svc1.predict(X1)
svc1.score(X1,y1.flatten())

# 2.2.2 误差项惩罚系数C=100
svc100 = SVC(C = 100,kernel = 'linear')#线性核函数
svc100.fit(X1,y1.flatten())
svc100.predict(X1)
svc100.score(X1,y1.flatten())

# 2.3 绘制决策边界
plt.figure(1)
plot_boundary(svc1, X1,'b')
plot_boundary(svc100, X1,'y')
plt.show

## part3 线性不可分SVM(决策边界清晰)

# 3.1 可视化数据
plt.figure(2)
plot_data(X2,y2)

# 3.2 设置参数
a1 = np.array([1, 2, 1])    
a2 = np.array([0, 4, -1])  
sigma = 2

# 3.3 使用高斯函数
gaussianKernel(a1, a2, sigma)

# 3.4 #训练模型（这里使用内置高斯核）
svc2 = SVC(C = 100,kernel = 'rbf',gamma=np.power(0.1, -2)/2)##对应sigma=0.1
svc2.fit(X2,y2)
 
svc2.predict([[0.4, 0.9]])
svc2.score(X2,y2.flatten())
 
# 3.5 绘制决策边界   
plt.figure(2)

ax = plot_boundary(svc2, X2, 'b')
plt.show

## part4 线性不可分SVM(决策边界不清晰)
#        在验证集上寻找最佳参数

# 4.1 可视化数据
plt.figure(4,figsize=(12.8,4.8))
plt.subplot(1,2,1)
plot_data(X3,y3)
plt.subplot(1,2,2)
plot_data(Xval,yval)

# 4.2 寻找最优参数C和gamma
gammas = [0.01,0.03,0.1,0.3,1,3,10,30,100]#9
Cvalues = [0.01,0.03,0.1,0.3,1,3,10,30,100]#9
best_score = 0
best_pramas = (0,0)
for c in Cvalues:
    for gamma in gammas:
        svc3 = SVC(c,kernel = 'rbf')
        svc3.fit(X3,y3)
        score = svc3.score(Xval,yval)
        if score > best_score:
            best_score = score
            best_pramas = (c,gamma)
 
print(best_score,best_pramas)#0.96 (30, 0.01)

# 4.3 绘制决策边界   
plt.figure(4)
plt.subplot(1,2,1)
plot_boundary(svc3, X3,'b')
plt.subplot(1,2,2)
plot_boundary(svc3, Xval,'b')
plt.show

运行结果如下：