Zama TFHE-rs白皮书（1）

1. 引言

前序博客有：

• 基于[Discretized] Torus的全同态加密指引（1）
• 基于[Discretized] Torus的全同态加密指引（2）
• TFHE——基于[Discretized] Torus的全同态加密 代码解析
• Zama TFHE-rs

Zama TFHE-rs白皮书，见：

• Zama团队Ilaria Chillotti、Marc Joye、Pascal Paillier论文《Programmable Bootstrapping Enables Efficient Homomorphic Inference of Deep Neural Networks∗》

很多情况下，人们认为机器学习和隐私是对立的。对于包含敏感数据的情况，隐私尤其受关注。本文实现了具有隐私保护的深度神经网络推理。
Zama TFHE-rs为首个TFHE全同态加密方案尝试，其底层关键技术为programmable bootstrapping：

• 支持对密文的任意函数的同态evaluation，具备可控的噪声。
• 与之前的成果相比，无需对模型进行重新训练。

本文基本结构为：

• 1）回顾一些有用概念的定义，以及确定一些标记法。
• 2）介绍了TFHE方案的离散化变种。同时详述了如何对密文做基础leveled operations。
• 3）展示了本文核心技术：programmable bootstrapping。首先介绍了常规bootstrapping，然后将其归纳为programmable bootstrapping。
• 4）将本文成果用于神经网络同态评估。 描述了常用于构建神经网络的不同layers，及其使用本文架构的实现。
• 5）汇总了一些试验和benchmarks。
• 6）本文结论。

1.1 机器学习革命

从数据中学习的基本前提是从一组观察结果中揭示一个过程。机器学习在提取有用信息方面非常有效，并且可在给定数据和期望目标的情况下动态适应特定任务。因此，与经典的统计方法不同，机器学习从数据本身学习模型的重要影响因素。

机器学习可开发许多应用程序：回归、分类、推荐、聚类、异常检测等等。如今，机器学习被广泛应用于各个行业，并提供多种服务，包括：

• 欺诈检测
• 风险管理
• 人脸识别
• 辅助驾驶
• 电子邮件分类
• 自动翻译
• 医疗诊断等。

1.2 隐私需求

机器学习算法在很多领域都很有用，但其处理的数据类型通常是敏感的。典型例子有：

• 根据DNA样本探测特定基因疾病
• 人脸识别
• 邮件分类等等。

这些例子中，机器学习算法所处理的数据包含了用户的私人信息，且可被用于很多其它场景——从广告定投，到，勒索，甚至某些情况下的威胁。这也是为何包含机器学习应用程序中所使用的数据是至关重要的。

处理用户数据的公司所必须遵守的最新法规（如欧洲的GDPR（通用数据保护条例）或美国的CCPA（加州消费者隐私法）），也推动了隐私要求。

1.3 全同态加密

对于数据保护，密码学技术是一种可选策略。但传统的加密算法只是在数据传输或静止时保护数据。事实上，传统加密方案的一个局限性和结构特性是：

• 数据在处理之前首先需要解密。

因此，传统加密方案 不适用于机器学习应用程序。

对于传统的加密方案，隐私控制权掌握在加密数据的接收者手中。一种根本不同的方法是依赖全同态加密（FHE）。FHE在1978年首次提出挑战，直到2009年Gentry的突破性结果才解决。与传统的加密方案相比，全同态加密方案允许接收方直接对加密数据进行操作。

基于FHE的方法非常适合机器学习即服务（MLaaS，Machine-learning-as-a-service）的用例。一个典型的应用场景如下图所示。它涉及用户将数据发送到为给定任务（如，医疗诊断）运行经过训练的模型的服务提供商（服务端）。

1.4 噪声控制

Gentry成果的核心在于自举（bootstrapping）技术。全同态加密方案的所有已知实例都会产生带噪声密文。对这些密文运行同态运算反过来又增加了所得密文中的噪声水平。在某个时刻，密文中存在的噪声可能变得太大，且密文不再是可解密的。支持预定噪声阈值的同态加密方案被称为leveled（或homomorphic）。bootstrapping是一种允许刷新密文的通用技术。因此，它能够将leveled同态加密方案转化为全同态加密方案，从而能evaluate密文上的任何可能函数。自举背后的关键思想是对解密电路进行同态evaluate。为了执行自举过程，必须提供（与用于产生密文的加密密钥相匹配的）解密密钥的加密，该加密被称为自举密钥。如下图所示：

Gentry论文之后的研究旨在提出新的方案或改进自举，以提高FHE在实践中的效率。最著名的结构是DGHV[13]、BGV[7]、GSW[18]及其变体。虽然相继提出的结构使自举更加实用，但它仍然构成了瓶颈（每次自举需要几分钟时间）。Ducas和Micciancio[15]后来设计了一种基于GSW类型方案的更快的自举，将自举时间缩短到了一瞬间。他们的技术得到了进一步的改进和完善，这导致了TFHE方案的发展[12]。

1.5 本文技术和贡献

本文基于state-of-the-art TFHE方案，并将TFHE技术扩展至深度神经网络的同态evaluate。

TFHE有2种运行方式：

• 1）leveled TFHE：支持线性组合和预定数量的乘积次数。leveled TFHE方式下，其evaluate operations会让噪声总是增长。
  • 可用于evaluate small-depth电路。
• 2）bootstrapped TFHE：一旦噪声超过特定阈值时，通过将噪声降到指定级别，可很好地控制噪声。此外，bootstrapped方式是可编程的，从而支持对更复杂函数的evaluate。对于具有large depth电路的问题，仅bootstrapped TFHE方式才是可行的。深度神经网络，就属于具有large depth电路的问题。

早期的研究成果，尝试使用全同态加密来对神经网络进行evaluate：

• cryptonets[14]为首个以此为目标的论文。其能够针对MNIST数据集在5层上进行同态推理[24]。为了限制噪声的增长，用平方函数代替了标准的激活函数。底层加密方案是YASHE[4]的leveled版本。
• 随后的许多论文都采用了类似的方法，并在各个方向上进行了改进。其中，值得一提的是iDASH竞赛的结果[20]，其目标是在基因组分析的背景下找到保护隐私的解决方案。最近两个版本的同态加密轨道的获胜解决方案（即2018年的[3，22]和2019年的[21]）都有共同点，都依赖于leveled同态加密。

然而，leveled解决方案在其可执行的任务类型方面受到固有的限制。特别是，在神经网络场景，leveled解决方案只能容纳具有适度层数的网络。在本文，想强调的是，depth不再一定是一个问题，深度神经网络实际上可以用同态来evaluate。对于一种特殊类型的网络，Bourse等人的一篇论文[6]已经指出了这一点：特别地，对于signals被限制在set $\{-1,1\}$ 且激活函数是sign函数的离散化神经网络。其可扩展构建的核心是TFHE方案的自适应，以便能够在自举步骤期间评估[非线性]sign函数。在最近的一项工作中，Boura等人[5]研究了全同态加密对classical经典深度神经网络的适用性。他们通过将正态分布中的噪声值添加到中间值来模拟噪声传播的影响，同时对模型进行清晰的评估。这些实验是用利用标准ReLU激活函数的模型进行的，但也用利用其FHE友好变体的模型进行。通过用FHE友好的average-pooling层替换max-pooling层来运行类似的实验。作为他们研究的结论，[5]的作者建议支持FHE友好操作，因为它们通常对噪声扰动更有弹性。

本文与之前的研究方向有所不同。本文不寻求设计新的操作或修改拓扑结构，以使某特定神经网络更适合基于FHE的实现。相反，本文坚持使用原始的神经网络模型。这提供了不需要重新训练新模型的巨大优势。由于操作和拓扑结构不变，已经训练好的模型可按原样使用。训练神经网络的努力不应被忽视。这是一项既昂贵又耗时的操作。此外，在许多情况下，生成新模型甚至是不可能的，因为这意味着可访问训练数据集，这可能需要数据所有者或一些监管机构的事先批准。

本文，通过可编程自举技术和分级操作（leveled operations）的结合，实现了对复杂函数的evaluate：

• 可编程意味着可获得输入密文的任何函数（包括非线性函数）作为自举的输出。有趣的是，生成的密文具有可控的噪声水平。因此，这个过程可以反复迭代。因此，在机器学习应用的情况下，神经网络的深度可以任意大。本文技术是高效的，可直接对选定大小的words进行操作。

2. 准备工作

2.1 Torus和Torus多项式

TFHE中的‘T’，是指real torus $\mathbb{T}=\mathbb{R}/\mathbb{Z}$，即为real numbers modulo $1$的集合。
$\mathbb{T}$中任意2个元素可added modulo $1$：$(\mathbb{T},+)$会形成一个abelian group。
但，$\mathbb{T}$不是ring，因未定义torus元素的internal product $\times$。

但定义了整数与torus元素的external product $\cdot$：

• 已知$k\in \mathbb{Z}$和$t\in \mathbb{T}$，元素$k\cdot t\in \mathbb{T}$定义为：
  • 若$k\ge 0$，则$k\cdot t=t+\cdots +t（|k|倍）$。
  • 若$k<0$，则$k\cdot t=(-k)\cdot (-t)=(-t)+\cdots +(-t)（|k|倍）$。
• 数学上，$\mathbb{T}$具有$\mathbb{Z}$-module结构，对于任意的$k,l\in \mathbb{Z}$和$a,b\in \mathbb{T}$，有：
  • $(k+l)\cdot a=k\cdot a+l\cdot a$
  • $k\cdot (a+b)=k\cdot a+k\cdot b$
• external product是同态的，对于任意的$k,l\in \mathbb{Z}$和$t\in \mathbb{T}$，有：
  $k\cdot (l\cdot t)=(kl)\cdot t$

定义torus多项式，以让密码学运算更可行。
令$\Phi :=\Phi (X)$表示$M$-th cyclotomic多项式（即，对于任意的$k<M$，可整除$X^M-1$而不是$X^k-1$，具有整数系数的唯一不可约多项式），以$N$来表示$\Phi :=\Phi (X)$ $M$-th cyclotomic多项式的degree。
基于性能考虑，选$M$为power of $2$，这样有$N=M/2$和$\Phi (X)=X^N+1$。
考虑多项式rings ${\mathbb{R}}_N[X]:=\mathbb{R}[X]/(X^N+1)$和${\mathbb{Z}}_N[X]:=\mathbb{Z}[X]/(X^N+1)$，定义${\mathbb{Z}}_N[X]$-module为：
${\mathbb{T}}_N[X]:={\mathbb{R}}_N[X]/{\mathbb{Z}}_N[X]=\mathbb{T}[X]/(X^N+1)$
即${\mathbb{Z}}_N[X]$元素，可看成是模$X^N+1$的多项式，该多项式的系数为real torus $\mathbb{T}$。

由于是${\mathbb{Z}}_N[X]$-module的，${\mathbb{T}}_N[X]$元素可相加，且与${\mathbb{Z}}_N[X]$多项式（外）乘。

向量可看成是行矩阵，并以粗体字表示。$\mathbb{Z}$或$\mathbb{T}$中元素以罗马字体表示，而多项式以书法体表示。

• $\mathbb{B}$为整数子集$\{0,1\}$。
• $N$为power of $2$。
• ${\mathbb{B}}_N[X]$为${\mathbb{Z}}_N[X]$中多项式子集，${\mathbb{B}}_N[X]$内元素多项式的系数为$\mathbb{B}$元素（即为$0$或$1$）。
• 向量$\mathbf{z}\in (\mathbb{Z}/q\mathbb{Z}{)}^n$，其norm $||\mathbf{z}||$定义为${\mathbb{Z}}^n$中$\mathbf{z}\in (\mathbb{Z}/q\mathbb{Z}{)}^n$等价classes之间的最短norm。
• ${\mathbb{Z}}_N[X]$中的多项式，可 以${\mathbb{Z}}^N$向量表示：即对于多项式$\mathfrak{p}=p_0+p_{1}X+\cdots +p_{N-1}{X}^{N-1}$，关联的向量为$(p_0,p_1,\cdots ,p_{N-1})$。
• 多项式的norm，定义为其关联向量的norm。

2.2 概率分布

将使用2种概率分布：

• 1）均匀分布uniform distribution，表示为$\mathcal{U}$。若均匀分布$\mathcal{U}$定义于间隔$[a,b]$，可表示为$\mathcal{U}[a,b]$。离散间隔以双括号表示为$[[a,b]]$。
• 2）高斯分布（又名正态分布）normal（a.k.a Gaussian）distribution，表示为$\mathcal{N}$。正态分布以均值$\mu$和方差${\sigma }^2$来表示为$\mathcal{N}(\mu ,{\sigma }^2)$。基于实数的正态分布，推导出，基于$\mathbb{Z}/q\mathbb{Z}$的离散化正态分布：对于实数$X\in \mathbb{R}$，对应某正数$Z=\lceil xq\rfloor (\mathrm{mod}q)$，其中$-q/2\le Z\le q/2$。

若$\mathcal{D}$为基于某space $S$的某分布，则$s\leftarrow \mathcal{D}(S)$表示$s$为根据$\mathcal{D}$从$S$中随机选择的，$s\leftarrow \mathcal{U}(S)$可简写为$s\stackrel{\S }{}S$。

2.3 复杂度假设

2005年，Regev [28] 引入了learning with errors（LWE）problem。并随后在[25, 30] 将其归纳扩展到ring结构。

TFHE的安全性依赖于：

• torus-based problems的hardness。此处的所谓torus-based problems，是指：
  • 基于torus的LWE假设
  • 和 基于torus的GLWE假设

Definition 1（基于torus的LWE难题）：

• 令$n\in \mathbb{N}$，$\mathbf{s}=(s_1,\cdots ,s_n)\stackrel{\S }{}{\mathbb{B}}^n$，$\mathcal{X}$为基于$\mathbb{R}$的error分布。基于torus的LWE难题，是指区分如下2种分布：
  ${\mathcal{D}}_0=\{(\mathbf{a},r)|\mathbf{a}\stackrel{\S }{}{\mathbb{T}}^n,r\stackrel{\S }{}\mathbb{T}\}$
  ${\mathcal{D}}_1=\{(\mathbf{a},r)|\mathbf{a}=(a_1,\cdots ,a_n)\stackrel{\S }{}{\mathbb{T}}^n,r={\sum }_{j=1}^n{s}_j\cdot a_j+e,e\leftarrow \mathcal{X}\}$

Definition 2（基于torus的GLWE难题）：

• 令$N,k\in \mathbb{N}$且$N$为power of $2$，$\mathfrak{s}=({\mathfrak{s}}_1,\cdots ,{\mathfrak{s}}_k)\stackrel{\S }{}{\mathbb{B}}_N[X{]}^k$，$\mathcal{X}$为基于${\mathbb{R}}_N[X]$的error分布。基于torus的GLWE难题，是指区分如下2种分布：
  ${\mathcal{D}}_0=\{(\mathfrak{a},\mathfrak{r})|\mathfrak{a}\stackrel{\S }{}{\mathbb{T}}_N[X{]}^k,\mathfrak{r}\stackrel{\S }{}{\mathbb{T}}_N[X]\}$
  ${\mathcal{D}}_1=\{(\mathfrak{a},\mathfrak{r})|\mathfrak{a}=({\mathfrak{a}}_1,\cdots ,{\mathfrak{a}}_k)\stackrel{\S }{}{\mathbb{T}}_N[X{]}^k,\mathfrak{r}={\sum }_{j=1}^k{\mathfrak{s}}_j\cdot {\mathfrak{a}}_j+e,e\leftarrow \mathcal{X}\}$

decisional LWE假设（或decisional GLWE假设），是指对于某安全参数$\lambda$，有$n:=n(\lambda ),\mathcal{X}:=\mathcal{X}(\lambda )$（或，$N:=N(\lambda ),k:=k(\lambda ),\mathcal{X}:=\mathcal{X}(\lambda )$），asserts断言，解决LWE难题（或GLWE难题）是不可行的。

3. 离散化TFHE

基于torus的LWE假设，是指，对于随机torus元素$r\in \mathbb{T}$，即使已知torus向量$(a_1,\cdots ,a_n)$，有很难将其与$r={\sum }_{j=1}^n{s}_j\cdot a_j+e$区分。
torus元素$r={\sum }_{j=1}^n{s}_j\cdot a_j+e$可用作隐藏“明文消息” $\mu \in \mathbb{T}$的random mask，从而构成密文：

• $\mathbf{c}=(a_1,\cdots ,a_n,r+\mu )\in {\mathbb{T}}^{n+1}$

其中：

• $s=(s_1,\cdots ,s_n)\in {\mathbb{B}}^n$承担私人加密密钥角色。
• 噪声$e$从正态错误分布$\mathcal{X}=\mathcal{N}(0,{\sigma }^2)$中随机采样。

相应的，基于torus的GLWE假设，是指，对${\mathbb{T}}_N[X]$的加密机制：

• 基于key $\mathfrak{s}=({\mathfrak{s}}_1,\cdots ,{\mathfrak{s}}_k)\stackrel{\S }{}{\mathbb{B}}_N[X{]}^k$ 对 $\mu \in {\mathbb{T}}_N[X]$的加密为：$\mathfrak{c}=({\mathfrak{a}}_1,\cdots ,{\mathfrak{a}}_k,\mathfrak{r}+\mu )\in {\mathbb{T}}_N[X{]}^{k+1}$

其中：

• $\mathfrak{r}={\sum }_{j=1}^k{\mathfrak{s}}_j\cdot {\mathfrak{a}}_j+e$
• 噪声$e$从基于${\mathbb{R}}_N[X]$的正态错误分布$\mathcal{X}=\mathcal{N}(0,{\sigma }^2)$中随机采样，即基于${\mathbb{R}}_N[X]$多项式，其系数源自$\mathcal{N}(0,{\sigma }^2)$。

[12]中指出，LWE-based密文，为GLWE-based密文的特例情况，即$(k,N)=(n,1)$。确实，当$N=1$时，有${\mathbb{R}}_N[X]=\mathbb{R},{\mathbb{Z}}_N[X]=\mathbb{Z},{\mathbb{T}}_N[X]=\mathbb{T}$。为让表述更通用，本文针对的GLWE设置，而LWE-based加密为GLWE的特例情况。

在大多数通用设置下，密文$\mathfrak{c}=({\mathfrak{a}}_1,\cdots ,{\mathfrak{a}}_k,\mathfrak{r}+\mu )$为基于${\mathbb{T}}_N[X]$的多项式向量。这些多项式也可看成是基于$\mathbb{T}$的向量。在实际实现中，torus元素以有限精度表示（通常为32位或64位）。令$\Omega$表示位精度，如$\Omega =32$，是指密文元素由32位精度表示。此时，torus元素限定为${\sum }_{i=1}^{\Omega }{t}_i\cdot 2^{-i}(\mathrm{mod}1)$格式，其中$t_i\in \{0,1\}$。

本质上，基于有限精度，是指替换$\mathbb{T}$为submodule：
$\hat{\mathbb{T}}:=q^{-1}\mathbb{Z}/\mathbb{Z}\subset \mathbb{T}$，其中$q=2^{\Omega }$。

且，计算是针对${\hat{\mathbb{T}}}_N[X]:=\hat{\mathbb{T}}[X]/(X^N+1)$。

将$\frac{1}{q}$看成是${\hat{\mathbb{T}}}_N[X]$中某元素，任意多项式$\mu \in {\hat{\mathbb{T}}}_N[X]$可写成：
KaTeX parse error: Undefined control sequence: \cdt at position 14: \mu=\bar{\mu}\̲c̲d̲t̲ ̲\frac{1}{q}

其中：

• $\bar{\mu }\in {\hat{\mathbb{Z}}}_N[X]$
• ${\hat{\mathbb{Z}}}_N[X]:=(\mathbb{Z}/q\mathbb{Z})[X]/(X^N+1)$

3.1 message编解码

加密之前的input message，可为任意格式。编解码的角色，是让input message与加密方案兼容。

在此，需引入一些术语：

• 1）cleartext，原文，是指特定有限message space $\mathcal{M}$中的原文$m$。
• 2）plaintext，明文，是指与加密算法匹配的明文，为将原文编码后的结果，如匹配$m$编码后的元素$\bar{\mu }\in {\hat{\mathbb{Z}}}_N[X]=Encode(m)$。
  对于任意的原文$m\in \mathcal{M}$，需满足$Decode(Encode(m))=m$。
• 3）ciphertext，密文。是指对明文的加密结果。

令$\bar{\mu }={\bar{\mu }}_0+{\bar{\mu }}_{1}X+\cdots +{\bar{\mu }}_{N-1}{X}^{N-1}\in {\hat{\mathbb{Z}}}_N[X]$为明文。因密文是待噪声的，该噪声添加到右侧（即低有效位），仅${\bar{\mu }}_i$的upper bits用于编码原文消息。特定同态运算，要求${\bar{\mu }}_i$的leading bits设置为$0$。
大多数情况下：

• 以$\bar{w}\ge 0$来表示leading bits数，又名padding bits数。
• 以$w\ge 1$，为实际表示input cleartexts的位数。即原文位数。
• 有$\bar{w}+w\le \Omega$。

定义$p=2^{\bar{w}+w}$：

• $w$为原文的位精度。
• $p$为原文的modulus。

明文多项式$\bar{\mu }\in {\hat{\mathbb{Z}}}_N[X]$的系数格式为${\bar{\mu }}_i=2^{\Omega -(\bar{w}+w)}({\bar{v}}_i\mathrm{mod}{2}^w)$，如下图所示：

对于任意元素$\bar{x}={\bar{x}}_H\frac{q}{p}\pm {\bar{x}}_L\in \mathbb{Z}/q\mathbb{Z}$，其中$0\le {\bar{x}}_L\le \frac{q}{2p}$，定义返回${\bar{x}}_H\frac{q}{p}$值的Upper函数：
$\mathbb{Z}/q\mathbb{Z}\to \mathbb{Z}/q\mathbb{Z},\bar{x}\mapsto Upper(\bar{x})$，其中：
$Uppe{r}_{q,p}(\bar{x})=\frac{q}{p}\lceil \frac{p\ast \text{lift}(\bar{x})}{q}\rfloor (\mathrm{mod}q)$

其中：

• $\text{lift}$ 函数，会将$\mathbb{Z}/q\mathbb{Z}$元素，lift到$\mathbb{Z}$元素。
• 通过对每个系数进行操作，$Upper$函数很自然地扩展为${\hat{\mathbb{Z}}}_N[X]$多项式。

特别地，但$q=2^{\Omega },p=2^{\bar{w}+w}$时，相应的$Upper$函数为：
$Uppe{r}_{q,p}(\bar{x})=2^{\Omega -(\bar{w}+w)}\lceil \frac{2^{\bar{w}+w}\ast \text{lift}(\bar{x})}{2^{\Omega }}\rfloor (\mathrm{mod}q)$。

注意，若$\bar{x}={\bar{x}}_H{2}^{\Omega -(\bar{w}+w)}\pm {\bar{x}}_L\in \mathbb{Z}/q\mathbb{Z}$，其中$0\le {\bar{x}}_L\le 2^{\Omega -(\bar{w}+w)-1}$，则$Uppe{r}_{q,p}(\bar{x})={\bar{x}}_H{2}^{\Omega -(\bar{w}+w)}$。

3.2 有限精度的GLWE加解密描述

以$\overline{GLWE}$来表示有限精度的TFHE加密方案，$\overline{LWE}$为$(k,N)=(n,1)$的特例情况。相应的加密方案关键算法有：

• 1）$KeyGen(1^{\lambda })$：输入为安全参数$\lambda$，整数$(k,N)$，其中$k\ge 1$，$N$为power of $2$。

  • 同时定义某基于${\mathbb{R}}_N[X]$的正态错误分布$\mathcal{X}=\mathcal{N}(0,{\sigma }^2)$。
  • 随机均匀采样获得向量$\mathfrak{s}=({\mathfrak{s}}_1,\cdots ,{\mathfrak{s}}_k)\stackrel{\S }{}{\mathbb{B}}_N[X{]}^k$。
  • 明文空间为${\hat{\mathbb{Z}}}_N[X]=(\mathbb{Z}/q\mathbb{Z})[X]/(X^N+1)$，其中$q=2^{\Omega }$，原文modulus为$p=2^{\bar{w}+w}$，有$\Omega \ge \bar{w}+w$。
  • 输出：
    • 公共参数为$pp=\{k,N,\sigma ,p,q\}$。
    • 私钥为$sk=\mathfrak{s}$。

• 2）$Encryp{t}_{sk}(\bar{\mu })$：对明文$\bar{\mu }\in {\hat{\mathbb{Z}}}_N[X]$的加密为：
  $$\begin{gathered} \bar{\mathfrak{c}}\leftarrow {\overline{GLWE}}_{\mathfrak{s}}(\bar{\mu }) \\ :=({\bar{\mathfrak{a}}}_1,\cdots ,{\bar{\mathfrak{a}}}_k,\bar{\mathfrak{v}})\in {\hat{\mathbb{Z}}}_N[X{]}^{k+1} \end{gathered}$$
  其中：

  • ${\bar{\mu }}^{\ast }=\bar{\mu }+\bar{e}(\mathrm{mod}(q,X^N+1))$
  • $\bar{\mathfrak{v}}={\sum }_{j=1}^k{\mathfrak{s}}_j{\bar{\mathfrak{a}}}_j+{\bar{\mu }}^{\ast }(\mathrm{mod}(q,X^N+1))$
  • $({\bar{\mathfrak{a}}}_1,\cdots ,{\bar{\mathfrak{a}}}_k)\stackrel{\S }{}{\hat{\mathbb{Z}}}_N[X{]}^k$ 为随机多项式向量。
  • 离散噪声$\bar{e}=\lceil eq\rfloor (\mathrm{mod}q)$，其中$e\leftarrow {\mathbb{R}}_N[X]$多项式系数从$\mathcal{N}(0,{\sigma }^2)$中随机采样。

• 3）$Decryp{t}_{sk}(\bar{\mathfrak{c}})$：使用私钥$\mathfrak{s}=({\mathfrak{s}}_1,\cdots ,{\mathfrak{s}}_k)$对$\bar{\mathfrak{c}}=({\bar{\mathfrak{a}}}_1,\cdots ,{\bar{\mathfrak{a}}}_k,\bar{\mathfrak{v}})$ 进行解码，计算${\hat{\mathbb{Z}}}_N[X]$：
  ${\bar{\mu }}^{\ast }=\bar{\mathfrak{v}}-{\sum }_{j=1}^k{\mathfrak{s}}_j{\mathfrak{a}}_j(\mathrm{mod}(q,X^N+1))$
  然后输出$Uppe{r}_{q,p}({\bar{\mu }}^{\ast })$。

正确性：
令$p=2^{\bar{w}+w},q=2^{\Omega }$，$\bar{\mu }={\bar{\mu }}_0+\cdots +{\bar{\mu }}_{N-1}{X}^{N-1}$，其中${\bar{\mu }}_i=\frac{q}{p}({\bar{v}}_i\mathrm{mod}{2}^w)$。若，$\bar{\mathfrak{c}}\leftarrow Encryp{t}_{\mathfrak{s}}(\bar{\mu })$，只要$||\bar{e}|{|}_{\infty }\le \frac{q}{2p}=2^{\Omega -(\bar{w}+w)-1}$。

对应Proof：
有${\bar{\mu }}^{\ast }=\bar{\mu }+\bar{e}$，其中$\bar{e}={\bar{e}}_0+\cdots +{\bar{e}}_{N-1}{X}^{N-1}$。因此，将${\bar{\mu }}^{\ast }$ lift到${\mathbb{Z}}_N[X]$，有$\lceil \frac{p}{q}{\bar{\mu }}^{\ast }\rfloor =\lceil \frac{p}{q}(\bar{\mu }+\bar{e})\rfloor ={\sum }_{i=0}^{N-1}\lceil \frac{p}{q}({\bar{\mu }}_i+{\bar{e}}_i(\mathrm{mod}q))\rfloor X^i={\sum }_{i=0}^{N-1}\lceil \frac{p}{q}({\bar{\mu }}_i+{\bar{e}}_i+q{\delta }_i)\rfloor X^i={\sum }_{i=0}^{N-1}(({\bar{v}}_i\mathrm{mod}{2}^w)+\lceil \frac{p}{q}{\bar{e}}_i\rfloor +p{\delta }_i)X^i$，其中${\delta }_i\in \mathbb{Z}$。
注意，若$||\bar{e}|{|}_{\infty }\le \frac{q}{2p}$，则$\lceil \frac{p}{q}{\bar{e}}_i\rfloor =0$，从而有$Uppe{r}_{q,p}({\bar{\mu }}^{\ast })\equiv \frac{q}{p}\lceil \frac{p}{q}{\bar{\mu }}^{\ast }\rfloor \equiv \frac{q}{p}{\sum }_{i=0}^{N-1}({\bar{v}}_i\mathrm{mod}{2}^w)X^i\equiv \bar{\mu }(\mathrm{mod}q)$。

Remark 1：
某些特定应用中，接受解密算法恢复的不是准确的初始明文，而是其近似值。此时，要求变为$Decryp{t}_{\mathfrak{s}}(\bar{\mathfrak{c}})\approx \bar{\mu }$，且对$||e|{|}_{\infty }$的限定条件也可放松。

3.3 Leveled operations

FHE支持直接对密文运算。取决于运算类型，最终噪声水平都或多或少将增加。

3.3.1 加法运算

$\overline{GLWE}$密文是加法同态的。

3.3.2 scalar multiplication运算

$\overline{GLWE}$密文与常量值（或多项式）的乘法运算是同态的。

3.3.3 external product运算

$\overline{GLWE}$密文不支持原生内乘运算，实际上，2个$\overline{GLWE}$密文无法直接相乘。
一种聪明的做法是使用基于矩阵的方法——GSW构建。$\overline{GGSW}$为通用GSW加密算法，$\overline{GSW}$为其特例情况，对应有$(k,N)=(n,1)$。

令参数$B=2^{\beta },\ell$，有$\beta ,\ell \ge 1$，使得$\ell \beta \le \Omega$。
同时定义向量$\mathbf{g}=(2^{\Omega -\beta },2^{\Omega -2\beta },\cdots ,2^{\Omega -\ell \beta })$。以$\overline{GLWE}$加密密钥$\mathfrak{s}\in {\mathbb{B}}_N[X{]}^k$，对明文$m\in {\mathbb{Z}}_N[X]$做$\overline{GGSW}$加密定义为：

其中：

• $\bar{\mathcal{I}}$矩阵中每行为对$0$的fresh $\overline{GLWE}$加密。
• ${\mathbf{G}}^T$称为gadget矩阵：【其中，${\mathbf{I}}_{k+1}$表示size为$k+1$的单位矩阵】
  
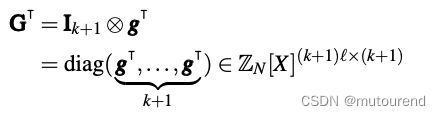
• 对于$\mathbb{Z}/q\mathbb{Z}$中的任意元素$d$，可将其看成是$[[-\frac{q}{2},\frac{q}{2}]]$范围内的整数，然后近似表示为a signed-digit radix-$B$ expansion of size $\ell$：
  $d\approx q{\sum }_{i=1}^{\ell }{d}_i{B}^{-i}={\sum }_{i=1}^{\ell }{d}_i{2}^{\Omega -i\beta }={\mathbf{g}}^{-1}(d){\mathbf{g}}^T$
  其中：
  • ${\mathbf{g}}^{-1}(d):=(d_1,\cdots ,d_{\ell })\in {\mathbb{Z}}^{\ell }$，其中digit $d_i\in [[-\frac{B}{2},\frac{B}{2}]]$。
  • 近似error限定为$|{\mathbf{g}}^{-1}(d){\mathbf{g}}^T-d|\le q/(2B^{\ell })=2^{\Omega -\beta \ell -1}$。

通过扩展，对于多项式$\mathfrak{p}=p_0+\cdots +p_{N-1}{X}^{N-1}\in {\hat{\mathbb{Z}}}_N[X]$，其系数可看成是$[[-\frac{q}{2},\frac{q}{2}]]$范围内的整数。
decomposition ${\mathbf{g}}^{-1}(\mathfrak{p})\in {\mathbb{Z}}_N[X{]}^{\ell }$，定义为：
${\mathbf{g}}^{-1}(\mathfrak{p})={\sum }_{j=1}^{N-1}{\mathbf{g}}^{-1}(p_j)X^j$。
显然$|{\mathbf{g}}^{-1}(\mathfrak{p}){\mathbf{g}}^T-\mathfrak{p}|\le 2^{\Omega -\beta \ell -1}$ 成立。

对于$k+1$个多项式组成的向量$\mathbf{p}=({\mathfrak{p}}_1,\cdots ,{\mathfrak{p}}_{k+1})\in {\hat{\mathbb{Z}}}_N[X{]}^{k+1}$，decomposition ${\mathbf{G}}^{-1}(\mathbf{p})\in {\mathbb{Z}}_N[X{]}^{(k+1)\times \ell }$定义为：
${\mathbf{G}}^{-1}(\mathbf{p})=({\mathbf{g}}^{-1}({\mathfrak{p}}_1),\cdots ,{\mathbf{g}}^{-1}({\mathfrak{p}}_{k+1}))$，且，$||{\mathbf{G}}^{-1}(\mathbf{p}){\mathbf{G}}^T-\mathbf{p}|{|}_{\infty }\le 2^{\Omega -\beta \ell -1}$。

有趣的是，$\overline{GLWE}$密文的gadget decomposition，可引起与$\overline{GGSW}$密文的外乘。
对于明文$m_1\in {\mathbb{Z}}_N[X]$和${\mu }_2\in {\hat{\mathbb{Z}}}_N[X]$，若${\bar{\mathfrak{C}}}_1\leftarrow {\overline{GGSW}}_{\mathfrak{s}}(m_1),{\bar{\mathfrak{c}}}_2\leftarrow {\overline{GLWE}}_{\mathfrak{s}}({\mu }_2)$，则二者的外乘$⊡$表示为：
${\bar{\mathfrak{c}}}_3={\bar{\mathfrak{C}}}_1⊡{\bar{\mathfrak{c}}}_2:={\mathbf{G}}^{-1}({\bar{\mathfrak{c}}}_2){\bar{\mathfrak{C}}}_1$

展开有：

从而可知，只要最终噪声（包括近似错误）保持small，则${\bar{\mathfrak{c}}}_3$是对$m_1\mu \in {\hat{\mathbb{Z}}}_N[X]$的$\overline{GLWE}$加密。

3.3.4 Cmux gate运算

以外乘为起点，可定义新的leveled运算：

• ‘controlled’ multiplexer，或CMux

CMux用作根据bit来做选择的selector，但其基于的是已加密数据。
CMux gate：

• 输入有：
  • 2个$\overline{GLWE}$密文${\bar{\mathfrak{c}}}_0$和${\bar{\mathfrak{c}}}_1$，分别对应明文${\mu }_0,{\mu }_1\in {\hat{\mathbb{Z}}}_N[X]$。
  • 1个对bit $b$的$\overline{GGSW}$密文$\bar{\mathfrak{C}}$。
• 输出为：
  • 对明文${\mu }_b$的$\overline{GLWE}$密文${\bar{\mathfrak{c}}}^{\prime }$，只要最终噪声keep small。

即CMux gate定义为：
${\bar{\mathfrak{c}}}^{\prime }\leftarrow CMux(\bar{\mathfrak{C}},{\bar{\mathfrak{c}}}_0,{\bar{\mathfrak{c}}}_1):=\bar{\mathfrak{C}}⊡({\bar{\mathfrak{c}}}_1-{\bar{\mathfrak{c}}}_0)+{\bar{\mathfrak{c}}}_0$

CMux gate在同态计算性能中（特别是bootstrapping中）承担核心角色，

FHE系列博客

• 技术探秘：在RISC Zero中验证FHE——由隐藏到证明：FHE验证的ZK路径（1）
• 基于[Discretized] Torus的全同态加密指引（1）
• 基于[Discretized] Torus的全同态加密指引（2）
• TFHE——基于[Discretized] Torus的全同态加密 代码解析
• 技术探秘：在RISC Zero中验证FHE——RISC Zero应用的DevOps（2）
• FHE简介
• Zama TFHE-rs