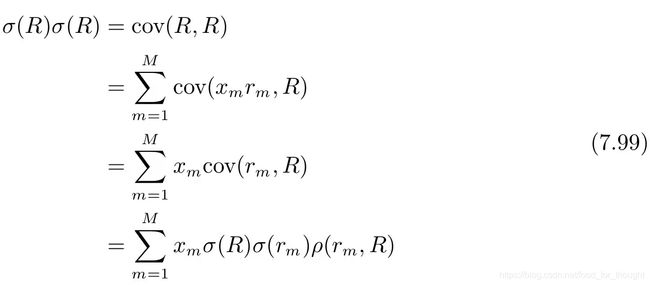【笔记】因子投资:方法与实践
文章目录
- 历史
- 宏观综述
-
- 研究角度
-
- 关于β'λ
- 关于α
- 截面角度vs时序角度
- 学术理论
-
- 基础概念
- 金融理论
-
- MM定理
- 资产定价模型
- 多因子模型
- 研究方法论
-
- 投资组合排序法
-
- 排序
- 检验
- 多重排序法
- 多因子模型的回归检验
-
- 时间序列回归
- 截面回归
- Fama-MacBeth回归
- 因子暴露和因子收益率
- 异象检验
- 多因子模型比较
-
- GRS检验
- α检验
- 因子正交化
- 广义矩估计
- 模型异象
-
- 多因子模型
-
- Fama-French 三因子模型
- Carchart 四因子模型
- Novy-Marx 四因子模型
- Fama-French 五因子模型
- Hou-Xue-Zhang 四因子模型
- Stambaugh-Yuan 四因子模型
- Daniel-Hirshleifer-Sun 三因子模型
- 异象
-
- 估值高低
-
- F-Score
- G-Score
- 基本面锚定反转
- 特质性波动率
- 研究现状
-
- p-hacking
-
- 先验
- 行为金融学解释异象与因子
- 其它
- 业界实践
-
- 收益率模型
- 投资组合优化
-
- 目标函数
- 约束条件
- 交易成本模型
- Smart Beta
- 因子择时
- 风格分析
- 风险归因
历史
1934年,Graham and Dodd 提出了价值溢价,Security Analysis也成为业界圣经。
1958年,Modigliani and Miller 提出了MM定理,该定理认为在不考虑税收、破产成本、信息不对称,且市场有效的假设下,企业价值不会因为企业融资方式改变而改变。
1964年,Sharpe 提出资产定价模型(Capital Asset Pricing Model, CAPM),清晰的绘出了风险和收益之间的关系,这个简单的关系为后续大量线性多因子定价模型的研究拉开了序幕,但这个模型在60年代很多人分别独立提出,如Treynor(1961, 1962), Lintner(1965), Mossin(1966),其中Sharpe和Lintner的最为知名。
1970年,Fama 提出联合假说(joint hypothesis)问题,即想要检验市场的有效性就必须先有一个合理的资产定价模型,自20世纪70年代以来,学术界在实证资产定价方面的研究都是在联合假说的框架下进行的。
1972年,Black 在CAPM的基础上加入一个zero-beta因子,提出不存在无风险资产也可以推导出另一个版本的CAPM模型。
1973年,Fama and Macbeth 在检验CAPM时,巧妙地规避了收益率随机扰动项截面相关性的影响,得到了更令人信服的结果并拒绝了CAPM模型,提出的回归方法得到了更广泛的传播,成了因子投资中的一个重要统计手段。
1976年,Ross 提出套利定价理论(Arbitrage Pricing Theory, APT),构建了线性多因子定价模型。
1977年,Basu 发现了便宜股效应。
1981年,Banz 发现了小市值效应。
1982年,Hansen 提出了广义矩估计(Generalized Method of Moments Estimator, GMM),常被用来检验多因子模型。
1984年,Shiller 提出了噪音交易者模型,成为了日后行为金融学文献的起点。
1989年,Gibbons 提出GRS检验。
1992年,Fama and French 整合了便宜股效应和小市值效应这些CAPM无法解释的异象。
1993年,Fama and French在市场因子的基础上加入了HML和SML两个因子,构成了一个三因子模型,目前它早已成为全球各国股票市场上实证资产定价研究的首选。Jegadeesh and Titman 提出动量效应。
1997年,Carhart 提出四因子模型。
2011年,John Cochrane 在美国金融协会主席演讲时用“因子动物园(factor zoo)”来描述因子研究的现状,并提出:哪些因子是独立的;哪些因子是重要的;因子驱动资产价格的原因是什么。
2013年,Novy-Marx 提出四因子模型。
2015年,Fama-French 提出五因子模型。Hou-Xue-Zhang 提出四因子模型。
2016年,Mclean and Pontiff 研究了97个因子在被发表后的表现,发现因子的收益率比论文中的表现降低了50%以上。
2017年,Stambaugh-Yuan 提出四因子模型。
2019年,Jegadeesh 研究了如何更准确的估计因子暴露,进而计算因子收益率。Liu 基于2000-2016年的数据发现A股市场规模效应显著,他为了正确估计规模溢价剔除了市值最小的30%的股票,而且使用EP取代BM构建了价值因子。
2020年,Daniel-Hirshleifer-Sun 提出了三因子模型。Fama and French 考察了排序法和回归法哪种计算的因子收益率能更好的解释股票预期收益率的截面差异。
宏观综述
研究角度
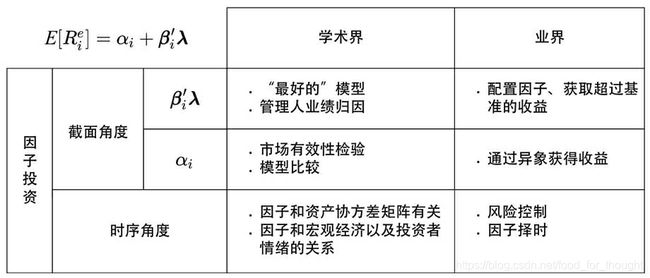
关于β’λ
学术界关注的是找到资产的α尽可能接近零,即该模型无法解释的异象越少越好;另外就是对主动基金管理人的业绩进行归因。
业界进行因子投资最重要的目标是使用因子来获取超过基准的收益,因此业界从资产配置的角度聚焦于找到长期来看有风险溢价的因子(λ大)并以尽可能高的暴露(β高)配置在这些因子上。
关于α
学术界从EMH观点出发,市场不应该存在太多异象;另外解释异象的能力是评价多因子模型优劣的重要标准之一。
业界看来,一个因子是否被纳入某个定价模型并不重要,而更关心在考虑了交易成本后,使用该因子是否能仍然获得超额收益。
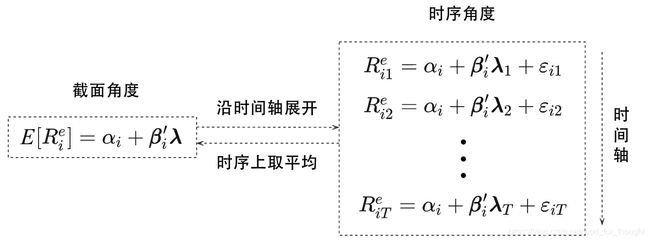
截面角度vs时序角度
从数学定义看,预期收益率是收益率在时间序列上的平均,因此均值的模型仅关心不同资产的收益率均值为什么会有差异,而非每个资产的收益率如何随时间变化。
在时序角度下,因子投资的两个重要问题是方差模型和因子择时。
学术理论
基础概念
- 因子:一个因子描述了众多资产共同暴露的某种系统性风险,该风险是资产收益率背后的驱动力;因子收益率是这种系统性风险的风险溢价或风险补偿,他是这些资产的共性收益。
- 异象:如果资产的实际预期收益率和多因子模型隐含的预期收益率之间的误差α显著不为零,则称这个资产为一个异象。
金融理论
MM定理
该定理认为在不考虑税收、破产成本、信息不对称,且市场有效的假设下,企业价值不会因为企业融资方式改变而改变。
资产定价模型
资产的预期超额收益由下面的一元线性模型决定:
E [ R i ] − R f = β i ( E [ R M ] − R f ) E[R_i]-R_f=\beta_i(E[R_M]-R_f) E[Ri]−Rf=βi(E[RM]−Rf)
式中, β i = c o v ( R i , R M ) / v a r ( R M ) \beta_i=cov(R_i, R_M)/var(R_M) βi=cov(Ri,RM)/var(RM) 刻画了该资产收益对市场收益的敏感程度,也被称为资产i对市场风险的暴露程度。
它指出资产的预期超额收益率由市场组合的预期超额收益率和资产对市场风险的暴露大小决定,而市场组合也被称为市场因子。
由于无风险利率自由借贷这一条件过分苛刻,Black提出了Black CAPM模型,是一个两因子模型:
E [ R i ] = β i E [ R M ] + ( 1 − β i ) E [ R Z ] E[R_i]=\beta_iE[R_M]+(1-\beta_i)E[R_Z] E[Ri]=βiE[RM]+(1−βi)E[RZ]
式中第二个因子被称为零β因子,cov(R_Z, R_M)=0,所隐含的资产预期收益率与β之间的关系相比之前来说更加平坦,也更符合实证的结果。
多因子模型
资产的预期超额收益由下面的多元线性模型决定:
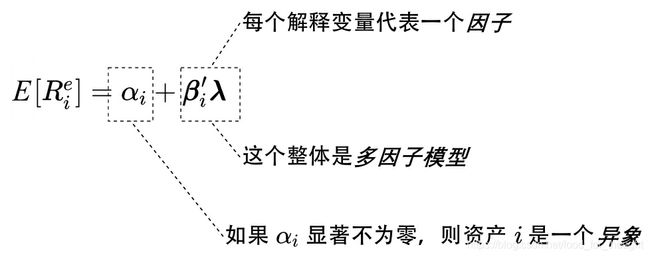
E [ R i e ] = α i + β i ′ λ E[R^e_i]=\alpha_i+\beta'_i\lambda E[Rie]=αi+βi′λ
其中β是资产的因子暴露(factor exposure)或称因子载荷(factor loading), λ是因子预期收益(factor expected return)或称因子溢价(factor risk premium)。
至于为什么代表超额预期收益的内容改变,是因为有很多常见的资产是通过多空对冲构建的资金中性投资组合,这类资产的预期超额收益就是多头和空头预期收益之差,无需额外减去无风险收益率。
如果α显著偏离零,则代表某个可以通过套利而获得超额收益的机会;也说明由于某些原因市场对该资产出现错误定价。
如何选择因子来构建多因子模型,如何计算资产在因子上的暴露以及因子的收益率,如何使用统计学的方法对定价误差α正式检验就成了使用多因子模型研究资产定价时必须回答的问题。也由此催生了一个全新的类别——因子投资(factor investing)
研究方法论
- 排序法
- 回归方法检验因子模型
- 计算因子暴露与因子收益率
- 检验异象
- 比较多因子模型
- 因子正交化
- 广义矩估计
投资组合排序法
因子模拟投资组合是使用股票资产、围绕某目标因子构建的投资组合,需要满足以下两个条件:
- 该投资组合仅在目标因子上有大于零的暴露、在其他因子上的暴露为零;
- 在所有满足条件一的投资组合中,该投资组合的特质性风险(idiosyncratic risk)最小。
对于一个满足条件一的投资组合,他的收益率由两部分驱动,分别为目标因子和构成该组合的个股的特质性风险,后者源自个股收益率在时序上的随机扰动。如果该组合中特质性风险很高,那么特质性风险的影响就会压过目标因子而占主导地位。
投资组合排序检验最重要的目的是检验因子预期收益率。原假设通常为因子预期收益率为零,因此检验关注的是依据样本数据计算出的因子收益率能否在给定的显著性水平下拒绝原假设。
排序
排序法最核心的思想是使用个股在排序变量上取值的大小来代替个股的在该因子上暴露的高低,仅假设变量和因子暴露是相关联的。因此人们虽然不知道个股在该因子上的暴露,但是却可以通过变量的高低代替他,也解释了为什么仅适用于风格因子。
- 排序:确定股票池并将股票池中的全部股票在截面上按照排序变量的取值高低排序。
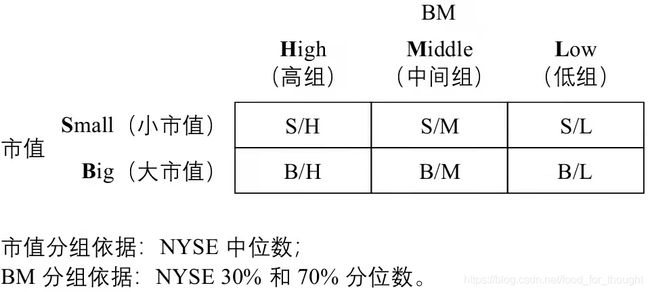
- 分组:按排名高低将全部股票分为L组(一般根据变量取值的十分位数分为十组,即L=10)。做多第一组,做空最后一组,该组合被称为价差组合(spread portfolio),价差组合的收益的差异反映了围绕该变量构建的因子的收益率,通常要求两个组合的资金是相同的,即资金中性,加权方式常见的是市值加权和等权重。
- 定期更新:即再平衡(rebanlance), 频率多为每月或每年。
检验
最重要的目的是检验因子预期收益率。
其中s.e.为标准误(standard error),上式说明讲λt在时序上取均值就可得到预期收益率的估计。以此进行t-检验。
另外可以关注依排序得到的收益率是否有单调性,可以计算收益率和排序变量分组的秩的相关系数(rank correlation coefficient)来检验。
多重排序法
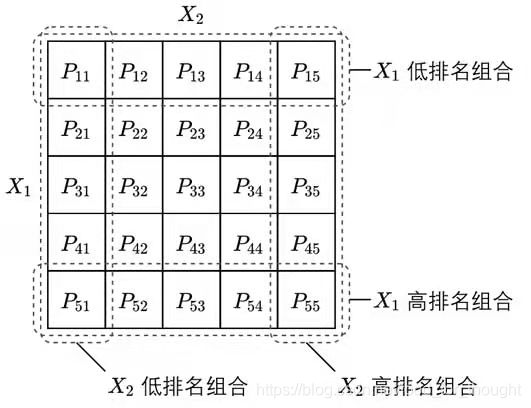
双重排序(double sorting or bivariate sorting),按照两个变量排序并构建因子模拟投资组合,目的是排除变量之间的相互影响从而更准确的计算收益率。变量X1和X2分别划分L1和L2组,一共得到L1×L2个组合。需要注意是对两个变量分别独立对股票排序,还是两个变量在排序时存在先后的依存关系,前者是独立双重排序,后者是条件双重排序。
独立双重排序使用两个排序变量分别独立的划分为L1和L2,两两取交集得到L1×L2个投资组合。缺点是可能导致某些组合包含的股票数目过少。
条件双重排序先用X1排序划分成L1组,再用X2排序进一步划分为L2个组。是考察X1被控制之后X2对股票收益率是否有增量信息,只需围绕第二个排序变量构建因子并计算因子收益率。有两种方法计算,第一种和前面的一样,第二种将L1个X2排名最高的组以及L1个X2排名最低的组取并集差分。等权重配置时两种方法完全等价,市值加权时略有差异。
多因子模型的回归检验
多因子模型中最核心的问题是检验一系列因子解释异象的能力,研究的核心问题是资产预期收益率在截面上(不同的资产)为什么有差异,因为根据模型来看,资产在因子上的暴露高则预期收益率也应该高。即最重要的是检验所以α联合起来是否在统计上足够接近零。
- 计算每个资产在所有因子上的暴露β
- 通过回归分析对多因子模型进行估计
- 联合检验资产定价误差α以及每个因子的预期收益率λ
时间序列回归
适合风格因子。
- 因子收益率时序需已知。使用因子收益率作为解释变量,分别对每个资产进行时序回归,得到该资产在这些因子上的暴露的估计β;时序回归中的α截距项就是截面关系上的定价误差。
- 将时序回归结果在时间上取均值,得到资产预期收益率和因子暴露在截面上的关系。由于时序回归是对每个资产单独进行的,因此该关系的确定不以最小化所有α的平方和为目标。
- 若ε满足IID(independent and identically distrubuted, 独立同分布)正态分布,则可以通过GRS方法构建F-统计量来检验α联合是否在统计上为零,否则可以通过广义矩估计等更高级的方法;对于因子预期收益率,可使用t-检验来分析。
截面回归
通常认为截面回归得到的因子收益率能够更加客观的评价因子风险溢价。
- 不要求因子收益率时间序列已知。通过时间序列回归得到每个资产i在因子上的暴露β,再进行截面回归,因此又被称作两步回归估计(two-pass regression estimate)
- 在得到β后使用资产的时序平均收益率E[R]和β进行截面OLS或GLS回归,估计出因子的期望收益率λ和资产定价误差α。
- 由于β是估计值,因此计算λ和α的标准误时可以进行Shanken修正。有了估计值和标准误则可以构建χ^2-统计量和t-统计量来检验。
Fama-MacBeth回归
- 是一种截面回归,第一步也是通过时间序列回归得到资产在因子上的暴露β。
- 得到β后在每个t使用OLS对资产超额收益率R和β的截面线性回归模型进行估计,得到t期因子的收益率的估计λ和残差的估计α。在通过T次截面回归得到T个估计后,将他们在时序上取均值得到因子预期收益率λ和残差均值α,此外利用这两个序列可计算cov(α)和σ(λ),以检验资产定价误差和因子预期收益率。
- 排除了α的截面相关性对标准误的影响,但对时序相关性无能为力。
因子暴露和因子收益率
由于时序回归得到的是β的估计,是非真实的,因此这种做法存在误差,将其作为解释变量就引入了计量经济学的变量误差(errors-in-variables, EIV),1973年论文的解决办法是使用个股组成的投资组合代替个股作为资产,会在一定程度上降低EIV的影响。
但2019年Jegadeesh的论文指出这种做法实际上是一种降维处理,会丢掉很多个股截面上的特征,如果待检验的因子和投资组合正交,则无法发现风险溢价,因此建议使用个股作为资产检验因子,引入了工具变量(instrumental variables, IV)应对EIV问题。
另外也有一种方法是直接采用公司特征的取值(经必要标准化)。
2020年Fama的论文表明截面回归多因子模型优于时序回归多因子模型:截面回归的因子收益率优于排序法的因子收益率,时变公司特征相比时序回归β是更好的因子暴露代理变量。
异象检验
时序回归检验异象:
- 选择一个潜在的财务指标或者量价指标,以它作为异象变量(anomaly variable)
- 根据异象变量取值的高低,将股票在截面上排序,使用排序法构建异象投资组合,并获得异象收益率的时间序列
- 检验该异象收益率能否被多因子模型解释
关于ε独立、同方差的问题:使用广义线性回归模型和White估计量、Newey-West估计量
- 使用异象收益率作为被解释变量、多因子中K个因子的收益率以及一个截距项作为解释变量,进行时序回归OLS估计,得到残差ε
- 使用K+1个解释变量X和残差ε,算出经Newey-West调整后的V_ols, 计算是按照1994年论文给出的公式确定最大滞后期数J
- 将V_ols的对角线元素开平方,其平方根就是回归系数b的标准误
- 找到截距项的标准误,它对应的就是α经Newey-West调整后的标准误s.e.(α),计算t-值进行t-检验
截面回归检验异象:
Fama-MacBeth截面回归也可以用于异象检验,因为异象能获得超额收益则意味着异象变量能够预测资产未来的收益率,而其可以在控制其他因子的同时,检验异象对收益率的预测性。
多因子模型比较
评价一个多因子模型时,联合检验多个资产定价误差是否为零就是第一种切入点,而单独考察这些资产的定价误差是否为零则是另一种切入点。前者可以采用GRS检验以及均值-方差张成(mean-variance spanning)检验,如果目标是把定价误差独立看待,则可以使用α检验。
GRS检验
- 它的F-统计量是有限样本下的统计量,是高度精确的。
- 具有非常高的检验效力。但其精确性依赖正态分布假设,实践中可能无法满足,同时要求样本数T大于资产数N。
α检验
将资产超额收益作为被解释变量,待检验的多因子模型作为解释变量,进行时序回归,估计定价误差α及其标准误,将所有资产的α和t-值的绝对值取平均作为评价依据。
因子正交化
正交意味着两个因子代表的资产收益的驱动力是不同的,即它们贡献了资产超额收益中不同的部分。
广义矩估计
对于解释变量与被解释变量是非线性的关系时,广义矩估计(Generalized Method of Moments, GMM)就可以大显身手了。它的核心最终能够归结为计算样本均值的方差。
- 把关注的问题表达成一系列总体矩条件,即提出模型。
- 使用样本数据得到对应的样本矩条件,从而对参数进行估计,即把模型和数据联系起来。
- 计算参数的标准误,并进行统计检验,即检验模型。
模型异象
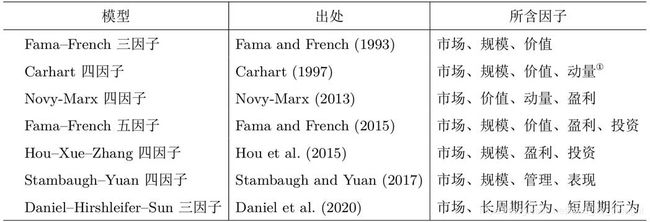
多因子模型
Fama-French 三因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , S M B E [ R S M B ] + β i , H M L E [ R H M L ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,SMB}E[R_{SMB}]+β_{i,HML}E[R_{HML}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,SMBE[RSMB]+βi,HMLE[RHML]
式中E[R_{SMB}]和E[R_{HML}]分别是规模因子和价值因子的预期收益率,β是个股在相应因子上的暴露。价值和规模因子分别选用BM和市值两个指标。
Carchart 四因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , S M B E [ R S M B ] + β i , H M L E [ R H M L ] + β i , M O M E [ R M O M ] E[R_i]−R_f=β_{i,MKT}(E[R_M]−R_f)+β_{i,SMB}E[R_{SMB}]+β_{i, HML}E[R_{HML}]+β_{i,MOM}E[R_{MOM}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,SMBE[RSMB]+βi,HMLE[RHML]+βi,MOME[RMOM]
式中MOM代表动量因子。加入了动量截面因子。
Novy-Marx 四因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , H M L E [ R H M L ] + β i , U M D E [ R U M D ] + β i , P M U E [ R P M U ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,HMLE}[R_{HML}]+β_{i,UMDE}[R_{UMD}]+β_{i,PMUE}[R_{PMU}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,HMLE[RHML]+βi,UMDE[RUMD]+βi,PMUE[RPMU]
式中PMU(Profitability-Minus-Unprofitaility)是盈利因子。作者指出盈利能力和未来预期收益密切相关,选用GP(Gross Profitability)毛利润。
Fama-French 五因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , S M B E [ R S M B ] + β i , H M L E [ R H M L ] + β i , R M W E [ R R M W ] + β i , C M A E [ R C M A ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,SMB}E[R_{SMB}]+β_{i,HML}E[R_{HML}]+β_{i,RMW}E[R_{RMW}]+β_{i,CMA}E[R_{CMA}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,SMBE[RSMB]+βi,HMLE[RHML]+βi,RMWE[RRMW]+βi,CMAE[RCMA]
式中RMW和CMA分别是盈利因子和投资因子。选用ROE和过去一年总资产变化率。
Hou-Xue-Zhang 四因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , M E E [ R M E ] + β i , I / A E [ R I / A ] + β i , R O E E [ R R O E ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,ME}E[R_{ME}]+β_{i,I/A}E[R_{I/A}]+β_{i,ROE}E[R_{ROE}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,MEE[RME]+βi,I/AE[RI/A]+βi,ROEE[RROE]
式中ME, I/A, ROE分别为规模因子、投资因子和盈利因子。选用市值、总资产变化率和ROE。是从实体投资经济学理论出发的,也被称为q-因子模型。
Stambaugh-Yuan 四因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , S M B E [ R S M B ] + β i , M G M T E [ R M G M T ] + β i , P E R F E [ R P E R F ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,SMB}E[R_{SMB}]+β_{i,MGMT}E[R_{MGMT}]+β_{i,PERF}E[R_{PERF}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,SMBE[RSMB]+βi,MGMTE[RMGMT]+βi,PERFE[RPERF]
式中MGMT和PERF分别为管理因子和表现因子。均源自关于错误定价的研究。
Daniel-Hirshleifer-Sun 三因子模型
E [ R i ] − R f = β i , M K T ( E [ R M ] − R f ) + β i , F I N E [ R F I N ] + β i , P E A D E [ R P E A D ] E[R_i]-R_f=β_{i,MKT}(E[R_M]-R_f)+β_{i,FIN}E[R_{FIN}]+β_{i,PEAD}E[R_{PEAD}] E[Ri]−Rf=βi,MKT(E[RM]−Rf)+βi,FINE[RFIN]+βi,PEADE[RPEAD]
式中FIN和PEAD分别代表长周期和短周期的两个行为因子。旨在捕捉由于过度自信和有限注意力造成的错误定价。
异象
估值高低
类似于PE\PB\PS\PCF(市盈率、市净率、市销率、市现率)这些价格乘数,表示价格偏离基本面的程度,越大表明估值越高,但实际中经常遇到市盈率很高但依然在涨和市盈率很低但依然在跌的情况,其实一个股票估值之所以便宜,是存在价格真的偏离了内在价值和本来就不值钱两种情况。
F-Score
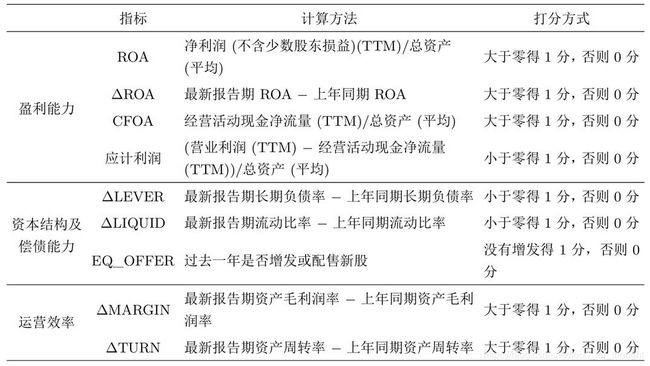
Piotroski 使用了三大类9个指标来度量一家公司的好坏:
G-Score
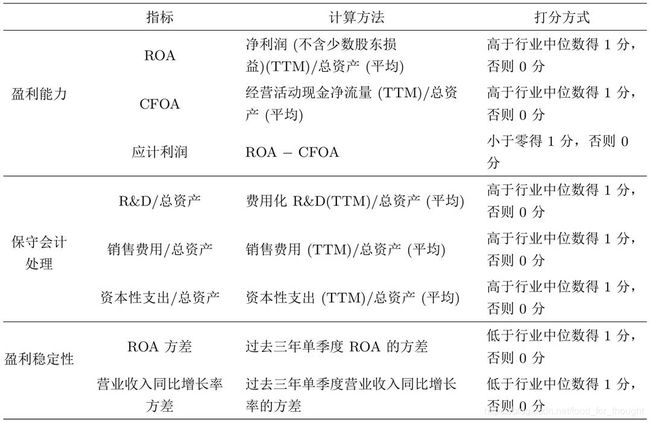
Mohanram 设计 G-Score 是从成长股(低BM)中区分出基本面好的赢家和基本面差的赢家,从而解决投资者面对高估值而错失亚马逊这种大牛股的问题:
其中保守会计准则指的是广告和研发等产生的支出往往被费用化处理,因而降低当期利润和现金流,这些支出与未来的盈利直接挂钩,投入越大未来潜力越大。
基本面锚定反转
短期反转现象(short-term reversal anomaly, STR)是A股中最显著的异象。意味着前期大涨的股票在未来有更低的预期收益率;反之同理。
股票超跌的原因通常有三个:基本面恶化;对信息的过度反应;噪音交易者导致的瞬时流动性冲击。其中第一个原则造成的大幅大跌很难反转。
特质性波动率
特质性波动率代表着特质性风险,经典理论认为特质性波动性和预期收益率之间应该相互独立,但大量实证表明二者之间表现出负相关性。
研究现状
p-hacking
在检验因子预期收益率时,p-值可以告诉人们能在何种显著性水平下拒绝原假设。
于是期刊编辑们倾向于接收低p-值因子的文章,学者们倾向于挖掘低p-值的因子。
p-值=prob(D|H0),因此不代表原假设或者备择假设是否为真,p-值是数据和假设之间关系的陈述,而非假设本身的陈述,即原假设H0成立的条件下,D发生的概率。并不是prob(H0|D)即在观测到D的前提下,原假设H0为真的条件概率。
先验
先验知识允许人们对每个潜在的因子赋予一个先验概率——比如告诉你按照股票代码首字母选股能获得超额收益,你一定会对它嗤之以鼻,因为如此选股没有科学逻辑支撑,先验概率非常低。使用先验概率,再结合检验的p-值就能得到因子是否显著的后验概率,这也是贝叶斯思想的一种体现。
下面有三个例子:(1)一位音乐家可区分莫扎特和海顿的乐谱,并连续成功地辨识了10张乐谱。(2)一个老妇人可判断出一杯奶茶里是先加奶还是先加茶,并连续成功地判断对了10杯。(3)一个老板说酒精赐予他预测未来的神力,并连续猜对10次扔硬币的结果。
在这三个例子中,如果原假设分别是音乐家无法辨识乐谱、老妇人不能识别茶和奶的加入顺序,以及酒馆老板不能预测扔硬币的结果,那么在原假设下,连续10次全部正确的结果的p-值是非常低的(远远低于0.001)。
但它们给人们的认知截然不同,这是因为先验。对于第一个例子,先验知识告诉人们音乐家分辨乐谱理应易如反掌,因此先验就是他能够成功,实验结果只是确认了这一点。在第二个例子中,人们则多少心存怀疑(先验),不相信老妇人能够成功,然而10次全对的结果让人们倾向于推翻自己的先验认知,即拒绝原假设,并认为她确实有这个能力。在第三个例子中,人们会认为酒精怎么能够预测未来?因此从心底完全不屑(先验)。在这种情况下,即便他猜对了10次,也不会推翻原假设(因为“酒精能够预测未来”这件事的先验概率太低了),而仅仅认为他是运气好罢了。从这三个例子能够看出先验在解读p-值时起到的作用,这就是贝叶斯思想的强大之处。
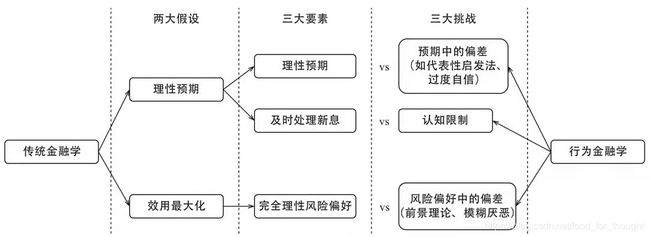
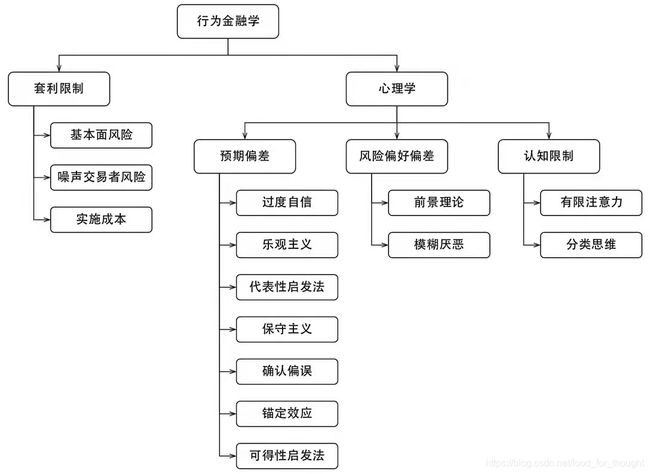
行为金融学解释异象与因子
其它
由于内容太多,只列举提纲:
- 投资者情绪
- 风险补偿、错误定价还是数据窥探
- 因子样本外失效风险
- 基本面量化投资
- 机器学习与因子投资
业界实践
收益率模型
寻找预测变量:1. 常见的行情数据和公司财务数据;2. 改进已有预测变量;3. 另类数据。
挑选预测变量:
IC是information coefficient的缩写,为信息系数,是主动管理领域最喜欢的指标。IR是信息率(information ratio).
收益率预测:参数化预测与非参数化预测
投资组合优化
目标函数
- 均值-方差优化
- 最小方差
- 最大多样化:最大化股票线性加权波动率与投资组合波动率之比
- 风险平价:让投资组合中的资产对组合的风险贡献相等,如全天候策略的核心是将投资组合的风险平均地暴露在不同的经济环境中
约束条件
- 卖空约束
- 杠杆约束
- 上下限约束
- 换手率约束
- 持仓数量约束
- 因子暴露约束
- 跟踪误差约束
交易成本模型
- 线性成本函数
- 二次成本函数
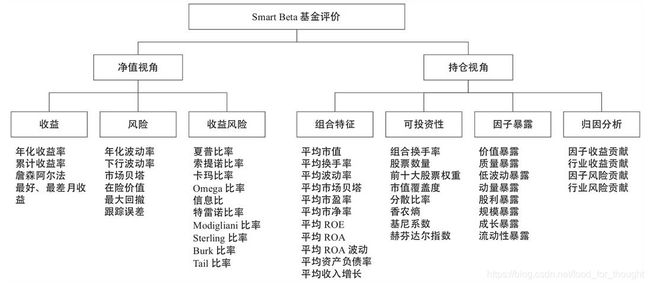
Smart Beta
Smart Beta:在某类资产里,以更高的收益或更低的风险为目标,针对一个或多个具有风险溢价的因子来确定投资组合持仓及权重。
被动投资认为市场是有效的,因此最好的方式是持有市场组合;主动投资认为市场不是完全有效,因此选股和择时是两个重要的思路,选股以在股票截面上选出未来预期收益率更高的股票为目标,而择时则以在时序上判断市场整体涨跌从而动态控制仓位为研究对象。
smart beta兼具以上两种流派基因,一方面属于典型的指数化投资,另一方面选择在特定的因子上有所暴露,主动偏离指数加权方式以获取更高收益或更低波动。
指数编制:
- 纯因子指数:为了正确定量计算因子的收益风险而从纯数学的角度构建的,没有考虑任何可投资性的约束
- 多空因子指数:资金量中性的
- 高暴露因子指数:会同时考虑因子暴露和可投资性的约束条件,通常为纯多头组合
- 高容量因子指数:不对股票筛选,权重同时考虑股票在因子上暴露的高低和股票自身市值大小
- 市场指数:按股票市值加权构建的指数,它对所有因子的暴露都是零
因子择时
用于因子择时的因素:
风格分析
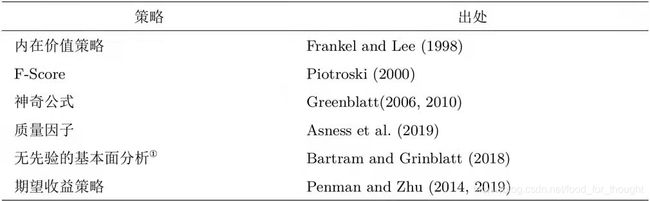
Hou et al. 进行风格分析的价值投资策略(agnostic fundamental analysis, AFA):
风险归因
Menchero and Davis 提出风险归因三要素公式:
笔记摘自于《因子投资:方法与实践》

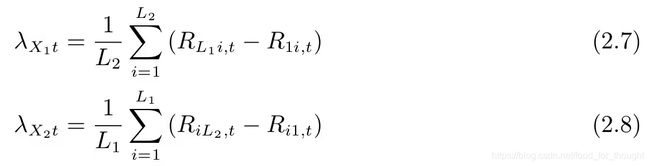
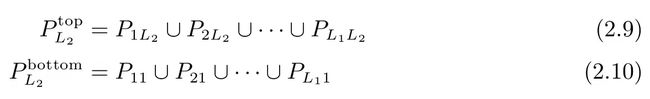
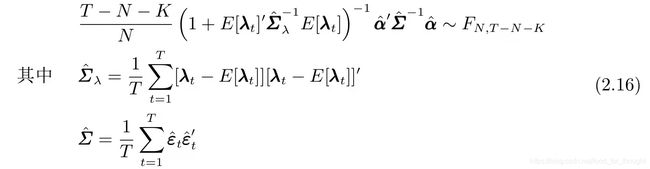
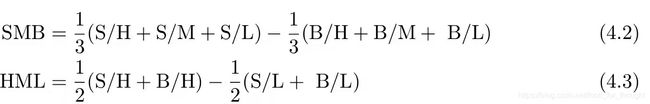
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-49qdJbr7-1611217475277)(因子投资/4.13.jpg)]](http://img.e-com-net.com/image/info8/9fbe6728af014563b83b5cd7f764e00f.jpg)