最短路合集，Dijkstra，堆优化Dijkstra，BellmanFord，SPFA，Floyd，附完整代码及OJ链接

前言

我们时常会面临着对路径选择的决策问题。例如在北京、上海、广州等城市，因其城市面积较大，乘地铁或公交都要考虑从A点到B点，如何换乘到达》现实中，每个人需求不同，选择方案就不尽相同。有人为了省钱，它需要的是路程最短(定价以路程长短为标准)，另一些人省时间为了要赶飞机火车或者早晨上班不迟到，他最大的需求是总时间要短；还有一类人，如老人行动不便，或者上班族下班，忙碌一天累得要死，他们都不想多走路，哪怕车子绕远路耗时长也无所谓，关键是换乘要少，这样可以在车，上好好休息一下。这些都是老百姓的需求，简单的图形可以靠人的经验和感觉，但复杂的道路或地铁网就需要计算机通过算法计算来提供最佳的方案。本文就要来研究关于图的最短路径的问题。

---

最短路径问题

若以带权图来表示真实的通讯、交通、物流或社交网络，则各边的权重可能代表信道成本、交通运输费用或交往程度。此时我们经常关心的一类问题，可以概括为:

给定带权网络G = (V, E)，以及源点(source) s ∈ V,对于所有的其它顶点v，s到v的最短通路有多长？该通路由哪些边构成?

---

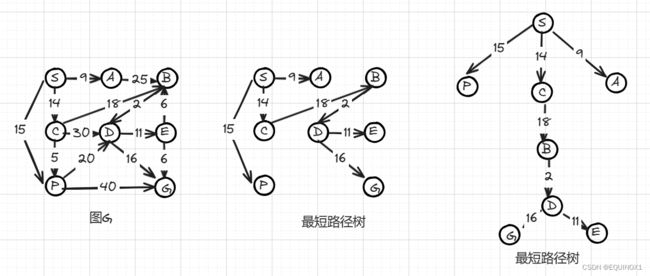
最短路径树

单调性

如下图所示，设顶点s到v的最短路径为ρ。于是对于该路径上的任一顶点u,若其在最短路径ρ上对应的前缀为σ，则σ也必是s到u的最短路径之一（注意是之一）。否则，若从s到u还有另一严格更短的路径τ，则易见ρ不可能是s到v的最短路径。

歧义性

即便各边权重互异，从s到v的最短路径也未必唯一。另外，当存在非正权的边，并导致某个环路的总权值非正时，最短路径甚至无从定义。因此，为了避免歧义，后续叙述时我们都假定图G中各边权为正值。

无环性

在下图所示的任意带权网络中，选取从源点到其余顶点的最短路径(若有多条，任选其一)。于是由以上单调性，这些路径的并集必然不含任何(有向)回路。这就意味着，它们应如图2和图3所示，构成所谓的最短路径树(shortest-path tree) 。

单源最短路算法

下面涉及到链式前向星存图，不熟悉的可以了解：一种实用的边的存储结构–链式前向星-CSDN博客

Dijkstra算法

Dijkstra ( 1930/05/11- 2002/08/06 )， 杰出的计算机科学家，1972年图灵奖得主

最短路径子树序列

将顶点ui到起点s的距离记作：dist[i] = dist(s, ui)， 1 ≤ i ≤ n。不妨设di按非降序排列，即di ≤ dj 当且仅当 i ≤ j。于是与s自身相对应地必有：u1 = s

我们下图中给定一棵最短路径树T(u1,u2,u3……un)，从T中删除(uk+1,uk+2……un)以及其关联的各边，得到的子图记作Tk，不难验证Tk一定是一棵树。归纳证明Tk具有连通性即可，由于u1到un为按照到源点s也就是u1的距离非降序排序，我们从Tk + 1到Tk删除的uk+1一定是叶子节点，而根据最短路径的单调性可知uk+1作为Tk + 1中到源点最远的节点是没有子节点的。

故而子树序列{T1 , T2 ……Tn}，构成了一个最短路径子树序列。

贪心迭代

我们颠倒上述过程，发现只要确定uk+1，就能从Tk扩展到Tk+1，故而，我们按照到s的距离进行非降序排序，逐一确定各个顶点{u1，u2，……，un}，最终就能得到我们的最短路径树Tn。

现在的问题在于，如何高效的找到uk+1？

Dijkstra的实现

实际上，由最短路径子树序列的上述性质，每一个顶点uk+1都是在Tk之外，距离s最近者。故我们以Tk外各顶点距离s的距离为优先级，每次选取**uk+1（Tk之外，距离s最近者）**加入Tk并将其拓展至Tk+1后，需要且只需要更新那些仍在Tk+1之外，且与Tk+1关联的顶点的优先级数。

可见Dijkstra与我们的最小生成树算法prim算法仅有一处差异，即前者考虑uk+1到s的距离，后者考虑uk+1到Tk的距离。

朴素Dijkstra

算法流程

• 到s距离数组dist，标记数组vis（用于记录是否已经进入Tk）

• 初始化dist[s] = 0

• 由于最短路径树只有n - 1条边，所以最多进行n - 1次迭代

• 每轮迭代从Tk外的节点，即未标记的节点中选出dist[u]最小的u

• 如果u不存在，说明已经得到最短路径树Tn，break

• 否则，标记u，对u的邻点进行松弛更新

• 算法结束，时间复杂度O(N^2)

  代码实现

void dijkstra(int s)
{
    vector dist(n + 1, inf);//inf为无穷大的数
    dist[s] = 0;
    bitset vis;

    for (int i = 1; i < n; i++)
    {
        int mind = INT_MAX, u = 0;
        for (int j = 1; j <= n; j++)
            if (!vis[j] && dist[j] < mind)
                u = j, mind = dist[j];
        if (!u)
            break;
        vis[u] = 1;

        for (int j = head[u]; ~j; j = edges[j].nxt)
        {
            int v = edges[j].v;
            if (vis[v])
                continue;
            if (dist[v] - edges[j].w > dist[u])
                dist[v] = dist[u] + edges[j].w;
        }
    }
    for (int i = 1; i <= n; i++)
        cout << dist[i] << " ";
}

堆优化Dijkstra

可见影响算法效率的大头就是uk + 1的选择，即然每次都选dist最小的节点，我们可以借助堆这一数据结构来快速选取，对Dijkstra进行优化。

• 到s距离数组dist，标记数组vis（用于记录是否已经进入Tk）
• 初始化dist[s] = 0，s进入优先级队列pq
• 如果pq非空，取出pq堆顶的节点u
• 如果pq已空，说明已经得到最短路径树Tn，break
• 否则，标记u，对u的邻点进行松弛更新，对于被更新的点进入pq
• 算法结束，时间复杂度O(NlogN)

代码实现

void dijkstra(int s)
{
    vector dist(n + 1, inf);
    dist[s] = 0;
    bitset vis;
    priority_queue, greater> pq;
    pq.emplace(0, s);
    while (pq.size())
    {
        auto [w, u] = pq.top();
        pq.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (int i = head[u]; ~i; i = edges[i].nxt)
        {
            int v = edges[i].v;
            if (vis[v])
                continue;
            if (dist[v] - edges[i].w > dist[u])
                pq.emplace(dist[v] = dist[u] + edges[i].w, v);
        }
    }
    for (int i = 1; i <= n; i++)
        cout << dist[i] << " ";
}

---

前面我们叙述时，提到了我们假定图G中各边权为正值。这也是最短路径树无环性的关键，那么如果出现某个回路总权值为负值，我们是否仍能用Dijkstra算法求解呢？或者说，我们是否仍能得到最短路径树呢？

很可惜，不能。假如出现了一个负环，那么就会导致在这个环上每走一圈就会导致环内点的dist值减小，此时用Dijkstra求解是没有意义的。所以我们需要一种能够判断负环的最短路径算法，于是有了BellmanFord算法和SPFA算法。

BellmanFord算法

BellmanFord算法由动态规划创始人Richard Bellman和数学家Lester Ford创立。

算法原理

也提到了Richard Bellman是动态规划的创始人，所以BellmanFord算法利用了动态规划思想不过分吧（bushi

一提动态规划大家一定就不困了（bushi

那么dist[i]如何进行状态转移呢？
$$dist[i]=dist[j]+w(j,i)，其中<j,i>\in E,dist[j]+w(i,j)<dist[i]$$
由于最短路径树只有n - 1条边，所以我们进行n - 1轮迭代，每次迭代遍历所有边进行状态转移，在没有负环的情况下是可以正确求解的，如果第n轮仍能进行状态转移，那么说明存在负环。

算法实现

算法流程

• 标记变量flag代表本轮迭代是否有状态更新
• dist数组存储到源点距离
• 进行n轮迭代，每轮迭代遍历所有边进行状态转移，flag初始为false
• 如果发生状态转移，那么flag = true
• 某次迭代后flag为false，说明dist已经是最终状态，return false，没有负环
• 迭代结束后，return flag，此时flag的值代表是否有负环
• 算法时间复杂度：（ne），n为节点数，e为边数

bool bellmanford(s)
{
    bool flag = false;
    memset(dist, inf, sizeof(dist));
    dist[s] = 0;
    for (int i = 0; i < n; i++)
    {
        flag = false;
        for (int u = 1; u <= n; u++)
        {
            if (dist[u] == inf)
                continue;
            for (int j = head[u]; ~j; j = edges[j].nxt)
            {
                int v = edges[j].v;
                if (dist[v] > dist[u] + edges[j].w)
                    dist[v] = dist[u] + edges[j].w, flag = true;
            }
        }
        if (!flag)
            return false;
    }
    return flag;
}

SPFA

段凡丁——SPFA的发明者。

SPFA已死

算法原理

SPFA是对BellmanFord的优化算法，即然BellmanFord是枚举所有边进行状态转移，但是并不是所有点都有资格进行状态转移的。不难分析出只有被本轮更新过的点下一轮才可能有资格对邻点进行更新，也就是说本轮你都没被更新，下一轮也轮不到你去更新别人，误人子弟（bushi。

即然对于每轮枚举的边有了限制，自然要引入辅助的数据结构了——队列，用于保存可能有资格更新邻接点的节点。

由于思想很简单，我们直接来看实现。

算法实现

算法流程

• 辅助队列q，dist数组存距离，cnt[i]存源点s到i的路径长度，标记数组vis存储是否在队列内

• 初始化s进队，dist[s] = cnt[s] = 0

• 获取队首元素u，如果dist[u]为无穷大，则跳过

• 否则遍历u的所有出边，邻接点v，如果dist[v] > dist[u] + edges[j].w，则更新dist[v]，cnt[v]

  • 如果更新后cnt[v] >= n，说明有负环，返回true

  • 否则如果v不在对内，那么v入队，打标记

• 队列空，返回false，无负环

• 算法最坏时间复杂度仍为O(VE)

多提一嘴，出题人有很多方法可以卡死SPFA，如链式菊花图，随机网格图，网格套菊花……（有兴趣自行了解）

bool spfa(int s)
{
    bitset vis;
    memset(dist, inf, sizeof(dist));
    memset(cnt, 0, sizeof(cnt));
    dist[s] = 0;
    queue q;
    q.emplace(s);
    while (q.size())
    {
        auto u = q.front();
        q.pop();
        vis[u] = 0;
        if (dist[u] == inf)
            continue;
        for (int j = head[u]; ~j; j = edges[j].nxt)
        {
            int v = edges[j].v;
            if (dist[v] > dist[u] + edges[j].w)
            {
                dist[v] = dist[u] + edges[j].w, cnt[v] = cnt[u] + 1;
                if (cnt[v] >= n)
                    return true;
                if (!vis[v])
                    q.emplace(v), vis[v] = 1;
            }
        }
    }
    return false;
}

多源最短路

你已经学会单源最短路了，相信你一定有思路跑出多源最短路。

跑n次堆优化Dijkstra，你别说也不是不行（

Floyd

美国计算机科学家Robert·Floyd于1962年提出，该算法同样基于动态规划的思想

Floyd可以说是众多板子中最好写最无脑的，邻接矩阵建图，三层for……就这没了？

最喜欢的一集

算法原理

其实学BellmanFord的时候你可能就有一种感觉，为什么不直接用这样一个转移方程
$$dist[i]=min(dist[i],dist[j]+dist[k])，其中i，j有路，j，k有路$$
因为我们前面存图用的都是链式前向星或者邻接表，直接找到像上面公式中的j，k是不方便的

所以求多源最短路需要用到邻接矩阵存图，自然也就要求了题目的数据量在1e3以内，不然炸了

算法原理也十分简单，一个简单的动态规划，枚举k作为中间节点，枚举i，j更新dist[i][j]即可

算法实现

算法流程

• 邻接矩阵g，初始化g[i][i] = 0，即每个节点到自己距离为0，其他都是inf（无穷大）
• 枚举k作为中间节点，枚举i，j
• 如果g[i][j] - g[i][k] > g[j][k]，那么更新g[i][j]
• 算法结束
• 时间复杂度：O(N^3)

复杂度不咋地，但是真的很好写啊orz

    cin >> n >> m;//顶点数目和节点数目
    for (int i = 0; i < m; i++)
    {
        cin >> u >> v >> w;
        g[v][u] = g[u][v] = w;
    }
    for (int i = 1; i <= n; i++)
        g[i][i] = 0;
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (g[i][j] - g[i][k] > g[j][k])
                    g[i][j] = g[i][k] + g[j][k];
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
            cout << g[i][j] << " ";
        cout << '\n';
    }

OJ链接

有一个SPFA会被卡哟

P4779 【模板】单源最短路径（标准版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P3371 【模板】单源最短路径（弱化版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

---

总结

对于正权图，我们一定可以得到一棵最短路径树，单调性和歧义性保证了最短路径数不唯一，而我们可以利用这两个性质求解出所有的最短路径（tip：动态规划）。单源最短路径，如果无负环无脑堆优化Dijkstra，其它两种看情况不会卡的话就用，卡的话一定有其他方法。多元最短路一般数据量小的时候直接打板子。

如果不总结，等于没总结