不容忽视的细节——线面积分中的奇点
不容忽视的细节——线面积分中的奇点
我写文章绝不是凭空而作，大部分是因为我做题的时候觉得这里掌握得不好。既然这个部分是自己的知识盲区，就需要我去认真复习。考研复习，一定要跳出自己的舒适圈。整天复习自己会的东西，做题目都索然无味，好像觉得自己都会了，结果做卷子一塌糊涂······
引子
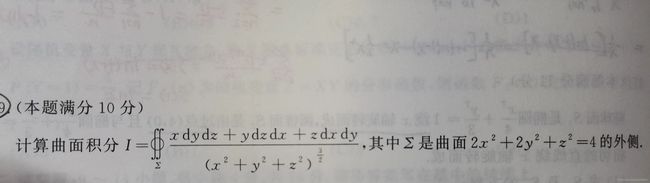
今天在做09年数一卷子的时候，这题给我难到了。大家可以先别往下看，试着做一下，答案是 4 π 4\pi 4π。什么？你做对了，那你可以点击右上角叉叉退出了哦
我们一看被积函数是具有轮换对称性的，那么我们就会想到利用高斯公式。很不幸分母特别讨厌，但不妨碍我们利用高斯公式
我靠！什么玩意？
∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ y = 0 \frac{\partial P}{\partial x} +\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial y}=0 ∂x∂P+∂y∂Q+∂y∂R=0
好了，三重积分结果为0。在考场上写完答案的你慌得一P，但你反复检查了很多遍发现求导没错，结果你这题的得分跟你结果一样QAQ。标准的错误，经典的零分
那么到底错在哪里？
回归课本
既然结果有问题，而计算没问题，那么我们往上一步，考虑一下高斯公式的使用条件吧。什么？高斯公式还有使用条件？我：立即推，放弃考研
课本中明确提到，在空间闭区域 Ω \Omega Ω内， P ( x , y , z ) , R ( x , y , z ) , Q ( x , y , z ) P(x,y,z),R(x,y,z),Q(x,y,z) P(x,y,z),R(x,y,z),Q(x,y,z)具有一阶连续偏导数。而题目中的被积函数很明显在(0,0,0)点连定义都没有，谈何连续偏导呢？那是不是说这个题不能用高斯公式了呢？不然。
既然(0,0,0)这个点没有定义，那我们把这个点扣掉，剩下的区域利用高斯公式不就完美了吗！！当然，不可能让你白白扣掉一个点呀，所以扣掉之后我们还需要单独算。也就成为：割补法
这道题就顺利的解决啦。当初问题就是出在我对高斯公式的使用条件不熟悉，忘记了被积函数在被积区域内有连续偏导（关键看是否有无定义的点）
提问：这里为什么曲面 Σ 1 \Sigma_1 Σ1取外侧，方向向内也符合条件呀
先自己思考，我在最后给出自己的想法
举一反三
曲面积分有，曲线积分也有。这里不得不提一下：单连通区域和复连通区域
相似的，我们可以类比高斯公式，格林公式也有类似的要求：
同样要求 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,y),Q(x,y)在D内有一阶连续偏导数（关键看是否有定义）
看一下课本这道例题
这题说L不经过原点，而被积函数在(0,0)点无定义，那么就有两种情况：
- 不包含原点，此时被积函数在L所围成的区域内是符合格林公式条件的
- 包含原点，此时(0,0)就不在被积函数的定义域内了，这时候就要使用我们的割补法
提问：这里为什么l的方向选取逆时针，顺时针可以吗？
课后练习
这是660上一道考察路径无关条件的题目，其中需要判断好单连通区域和复联通区域。可以试一试。
关于我的想法
1.我们可以看到课本中定义 Ω \Omega Ω是闭曲面的外侧，所以我们构造的封闭曲面的方向是指向外侧。 Σ 1 \Sigma_1 Σ1取外侧，那么相当于你在球体内部挖去一个方向向外的小球体。那么原来球体内部整体没有方向，所以挖去小球体后露出的表面方向也应该是向外，因为只有这样才能中和掉方向向外的 Σ 1 \Sigma_1 Σ1。
2.不可以。l的方向取逆时针，保证
∮ L − ∮ l = ∬ D x y \oint_{L}^{} -\oint_{l}^{} =\iint\limits_{D_{xy}}^{} ∮L−∮l=Dxy∬
所计算的区域是除去无定义点剩下的区域。也就是说，l的逆时针方向对于D来说是正方向。
总结
下次做题别再一上来立马格林公式和高斯公式了，先睁大眼睛看看，能用不能用不能用不？万一真的有奇点，补面或者补线的时候，想好方向：
- 曲线积分补线的方向是对于无定义点的区域来说是正方向
- 曲面积分补面的方向是外侧
关于积分与路径无关的四条等价结论，也熟悉熟悉。
多总结，总会发现新的东西。