【数字信号处理】FFT
FFT
2023年11月18日
#elecEngeneer
【数字信号处理】DFT
文章目录
- FFT
-
- 1. 快速傅里叶变换-FFT
-
-
- 1.1 时间抽取FFT(Decimation-in-time algorithm)
- 1.2 FFT做多项式乘法(卷积)
-
-
- 1.2.1 多项式乘法与卷积
- 1.2.2 多项式与DFT
- 1.2.3 多项式乘法与FFT
-
-
- 下链
1. 快速傅里叶变换-FFT
由于乘法是最慢的操作,衡量DFT在计算机上的标准就是乘法是数量。在前面的分析中DFT可以看成是矩阵乘以向量,所以乘法数量是 N 2 {N^2} N2 , N {N} N 是采样点的个数,也是变换的长度,对于大多数稳态, N {N} N 被选为最少是 256 {256} 256 ,来获得对信号有良好近似的频谱,计算速度也因此变得非常重要。
上世纪60年代中期开始,高效率执行DFT的算法逐渐出现。这些算法就是FFT算法,这些算法基于一个事实,即DFT存在大量冗余的计算。
将DFT写成:
F [ k ] = DFT ∑ n = 0 N − 1 f [ n ] W N k n , k = 0 , 1 , ⋯ , N − 1 F[k] \stackrel{\text{ DFT }}{=} \sum_{n=0}^{ N-1} f[n]W_N^{ kn} \,\,,\,\, k=0,1, \cdots ,N-1 F[k]= DFT n=0∑N−1f[n]WNkn,k=0,1,⋯,N−1
W N = e − j 2 π N W_N=e^{-j\frac{\large 2\pi}{\large N}} WN=e−jN2π
[!quote]- DFT矩阵
[ F [ 0 ] F [ 1 ] F [ 2 ] ⋮ F [ k ] ⋮ F [ N − 1 ] ] = [ 1 1 1 1 ⋯ 1 1 W W 2 W 3 ⋯ W N − 1 1 W 2 W 4 W 6 ⋯ W 2 ( N − 1 ) 1 W 3 W 6 W 9 ⋯ W 3 ( N − 1 ) ⋮ 1 W k W 2 k W 3 k ⋯ W k ( N − 1 ) ⋮ 1 W N − 1 W 2 ( N − 1 ) W 3 ( N − 1 ) ⋯ W ( N − 1 ) ( N − 1 ) ] [ f [ 0 ] f [ 1 ] f [ 2 ] ⋮ f [ n ] ⋮ f [ N − 1 ] ] \begin{bmatrix} F[0]\\ F[1]\\ F[2]\\ \vdots \\ F[k]\\ \vdots \\ F[N-1] \end{bmatrix}= \begin{bmatrix} 1&1&1&1& \cdots &1\\ 1&W&W^2&W^3& \cdots & W^{N-1}\\ 1&W^2&W^4&W^6& \cdots & W^{2(N-1)}\\ 1&W^3&W^6&W^9& \cdots & W^{3(N-1)}\\ \vdots \\ 1&W^{k}&W^{2k}&W^{3k}& \cdots & W^{k(N-1)}\\ \vdots \\ 1&W^{N-1}&W^{2(N-1)}&W^{3(N-1)}& \cdots & W^{(N-1)(N-1)}\\ \end{bmatrix} \begin{bmatrix} f[0]\\ f[1]\\ f[2]\\ \vdots \\ f[n]\\ \vdots \\ f[N-1] \end{bmatrix} F[0]F[1]F[2]⋮F[k]⋮F[N−1] = 1111⋮1⋮11WW2W3WkWN−11W2W4W6W2kW2(N−1)1W3W6W9W3kW3(N−1)⋯⋯⋯⋯⋯⋯1WN−1W2(N−1)W3(N−1)Wk(N−1)W(N−1)(N−1) f[0]f[1]f[2]⋮f[n]⋮f[N−1]
从DFT矩阵可以看出,相同的 W N k n {W_N^{kn}} WNkn 会被计算很多次,比如 k n = 16 {kn=16} kn=16 ,可能有
n = 2 , k = 8 n = 8 , k = 2 n = 1 , k = 16 n = 16 , k = 1 n = 4 , k = 4 \begin{align*} n=2 \,\,,\,\, &k=8\\ n=8 \,\,,\,\, &k=2\\ n=1 \,\,,\,\, &k=16\\ n=16 \,\,,\,\, &k=1\\ n=4 \,\,,\,\, &k=4 \end{align*} n=2,n=8,n=1,n=16,n=4,k=8k=2k=16k=1k=4
这几种情况,而且 W N {W_N} WN 的整数幂是一个周期为 N {N} N 的函数,只有 N {N} N 个确定的值。比如 N = 8 {N=8} N=8 (FFT最简单的时候 N {N} N 是 2 {2} 2 的整数幂):
W 8 1 = e − j 2 π / 8 = e − j 45 ° = 1 − j 2 = a W_8^1=e^{-j2\pi/8}=e^{-j45°}= \frac{1-j}{\sqrt{2}}=a W81=e−j2π/8=e−j45°=21−j=a
a 1 = a , a 2 = − j , a 3 = − j a = − a ∗ , a 4 = − 1 , a 5 = − a , a 6 = j , a 7 = j a = a ∗ , a 8 = 1 , a 9 = a 8 a = a \begin{array}{cccccc} a^1 = a,&a^2=-j,&a^3=-ja=-a ^{*}, &a^4=-1,\\ a^5=-a,&a^6=j,&a^7=ja=a ^{*} ,&a^8=1, \\ a^9=a^8a=a \end{array} a1=a,a5=−a,a9=a8a=aa2=−j,a6=j,a3=−ja=−a∗,a7=ja=a∗,a4=−1,a8=1,
所以:
W 8 4 = − W 8 0 W 8 5 = − W 8 1 W 8 6 = − W 8 2 W 8 7 = − W 8 3 \begin{align*} W_8^4=&-W_8^0\\ W_8^5=&-W_8^1\\ W_8^6=&-W_8^2\\ W_8^7=&-W_8^3 \end{align*} W84=W85=W86=W87=−W80−W81−W82−W83
实际上 W N {W_N} WN 就是个幅值为 1 {1} 1 的复数。 N {N} N 相当于把复平面上的单位圆分成 N {N} N 等分,如下图:

注意,从定义可知 W N x {W_N^x} WNx 是逆时针排列的!!!
对于复数,负号相当于旋转 180 ° {180°} 180° ,当 N {N} N 为 2 {2} 2 的整数幂时, W N x {W_N^x} WNx 存在落在坐标轴上的点。
1.1 时间抽取FFT(Decimation-in-time algorithm)
也叫“库利-图基算法”。将DFT采样序列中 n {n} n 为偶数和 n {n} n 为奇数的项分开,设 N {N} N 为 2 {2} 2 的整数次幂,则分开后的偶数项和奇数项各有 N / 2 {N/2} N/2 个:
F [ k ] = DFT ∑ n = 0 N − 1 f [ n ] W N k n = ∑ m = 0 N / 2 − 1 f [ 2 m ] W N k 2 m + ∑ m = 0 N / 2 − 1 f [ 2 m + 1 ] W N k ( 2 m + 1 ) \begin{align*} F[k] \stackrel{\text{ DFT }}{=}& \sum_{n=0}^{ N-1} f[n]W_N^{ kn} \\ \\ =& \sum_{m=0}^{ N/2-1} f[2m]W_N^{k2m}+\sum_{m=0}^{ N/2-1} f[2m+1]W_N^{k(2m+1)} \end{align*} F[k]= DFT =n=0∑N−1f[n]WNknm=0∑N/2−1f[2m]WNk2m+m=0∑N/2−1f[2m+1]WNk(2m+1)
而
W N k 2 m = e − j 2 π N 2 m k = e − j 2 π N / 2 m k = W N / 2 k m W_{N}^{k2m}=e^{-j\frac{\large 2\pi}{\large N}2mk}= e^{-j\frac{\large 2\pi}{\large N/2}mk}=W_{N/2}^{km} WNk2m=e−jN2π2mk=e−jN/22πmk=WN/2km
F [ k ] = ∑ m = 0 N / 2 − 1 f [ 2 m ] W N / 2 k m + W N k ∑ m = 0 N / 2 − 1 f [ 2 m + 1 ] W N / 2 k m F[k]=\sum_{m=0}^{ N/2-1} f[2m]W_{N/2}^{km}+W_N^{k}\sum_{m=0}^{ N/2-1} f[2m+1]W_{N/2}^{km} F[k]=m=0∑N/2−1f[2m]WN/2km+WNkm=0∑N/2−1f[2m+1]WN/2km
F [ k ] = G [ k ] + W N k H [ k ] F[k]=G[k]+W_N^kH[k] F[k]=G[k]+WNkH[k]
因此 N {N} N 个采样点的DFT可以由两个 N / 2 {N/2} N/2 个采样点的DFT计算得到,其中一个使用的是偶数的采样点,另一个使用的是奇数的采样点。计算量显然减少了。对于 N = 8 {N=8} N=8 :
{ 偶数的采样点 : f [ 0 ] , f [ 2 ] , f [ 4 ] , f [ 6 ] 奇数的采样点 : f [ 1 ] , f [ 3 ] , f [ 5 ] , f [ 7 ] \begin{cases} 偶数的采样点: f[0],f[2],f[4],f[6]\\ \\ 奇数的采样点: f[1],f[3],f[5],f[7] \end{cases} ⎩ ⎨ ⎧偶数的采样点:f[0],f[2],f[4],f[6]奇数的采样点:f[1],f[3],f[5],f[7]
F [ 0 ] = G [ 0 ] + W 8 0 H [ 0 ] F [ 1 ] = G [ 1 ] + W 8 1 H [ 1 ] F [ 2 ] = G [ 2 ] + W 8 2 H [ 2 ] F [ 3 ] = G [ 3 ] + W 8 3 H [ 3 ] F [ 4 ] = G [ 0 ] + W 8 4 H [ 0 ] = G [ 0 ] − W 8 0 H [ 0 ] F [ 5 ] = G [ 1 ] + W 8 5 H [ 1 ] = G [ 1 ] − W 8 1 H [ 1 ] F [ 6 ] = G [ 2 ] + W 8 6 H [ 2 ] = G [ 2 ] − W 8 2 H [ 2 ] F [ 7 ] = G [ 3 ] + W 8 7 H [ 3 ] = G [ 3 ] − W 8 3 H [ 3 ] \begin{align*} F[0]=&G[0]+W_8^0H[0]\\ F[1]=&G[1]+W_8^1H[1]\\ F[2]=&G[2]+W_8^2H[2]\\ F[3]=&G[3]+W_8^3H[3]\\ F[4]=&G[0]+W_8^4H[0]=G[0]-W_8^0H[0] \\ F[5]=&G[1]+W_8^5H[1]=G[1]-W_8^1H[1] \\ F[6]=&G[2]+W_8^6H[2]=G[2]-W_8^2H[2] \\ F[7]=&G[3]+W_8^7H[3]=G[3]-W_8^3H[3] \\ \end{align*} F[0]=F[1]=F[2]=F[3]=F[4]=F[5]=F[6]=F[7]=G[0]+W80H[0]G[1]+W81H[1]G[2]+W82H[2]G[3]+W83H[3]G[0]+W84H[0]=G[0]−W80H[0]G[1]+W85H[1]=G[1]−W81H[1]G[2]+W86H[2]=G[2]−W82H[2]G[3]+W87H[3]=G[3]−W83H[3]
FFT的数据流图如下:
由于 N {N} N 是 2 {2} 2 的整数幂, N / 2 {N/2} N/2 仍然是偶数,因此可以继续将 G [ k ] {G[k]} G[k] 分成两个变换组成, H [ k ] {H[k]} H[k] 也分成两个变换组成,每个变换含有 N / 4 {N/4} N/4 个采样点。
可见,时间抽取FFT可以将DFT递归地分解成许多小的变换。
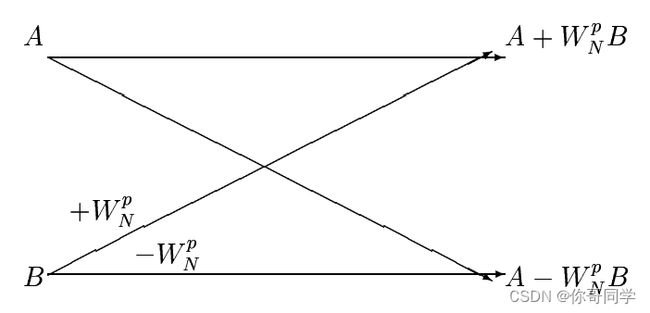
A {A} A 和 B {B} B 是复数,因此一个蝴蝶式的计算需要一个复数乘法( W N p B {W_N^pB} WNpB )和两个复数加法。
一个重要的发现,或者技巧,就是分解到最后,采样序列的索引是 位反转(bit-reversed) 的,如下表

对于 N {N} N 个采样点,DFT需要 N 2 {N^2} N2 个复数乘法,FFT需要大约 N 2 log 2 ( N ) { \frac{N}{2}\log_2(N)} 2Nlog2(N) 个。
[!example]-
f : [ 8 , 4 , 8 , 0 ] f:[8,4,8,0] f:[8,4,8,0]
F [ 0 ] = 16 + W 4 0 ⋅ 4 = 20 F [ 1 ] = 0 + W 4 1 ⋅ 4 = − 4 j F [ 2 ] = 16 + W 4 2 ⋅ 4 = 12 F [ 3 ] = 0 + W 4 3 ⋅ 4 = 4 j \begin{align*} F[0]=&16+W_4^0 \cdot 4 =20\\ F[1]=&0+W_4^1 \cdot 4=-4j \\ F[2]=&16+W_4^2 \cdot 4=12\\ F[3]=&0+W_4^3 \cdot 4=4j \end{align*} F[0]=F[1]=F[2]=F[3]=16+W40⋅4=200+W41⋅4=−4j16+W42⋅4=120+W43⋅4=4j
1.2 FFT做多项式乘法(卷积)
1.2.1 多项式乘法与卷积
序列的卷积 两个序列 f [ n ] , n = 0 : ( M − 1 ) {f[n],n=0:(M-1)} f[n],n=0:(M−1) 和 g [ n ] , n = 0 : ( N − 1 ) {g[n],n=0:(N-1)} g[n],n=0:(N−1) 的卷积,表示 g {g} g 滑过 f {f} f 时依据这些点确定的重叠部分的面积。
如果 M < N {M
( f ∗ g ) [ k ] = ∑ n = 0 k f [ n ] g [ k − n ] , k = 0 , 1 , ⋯ , 2 N − 2 (f*g)[k]= \sum_{n=0}^{k}f[n]g[k-n] \,\,,\,\, k=0,1, \cdots ,2N-2 (f∗g)[k]=n=0∑kf[n]g[k−n],k=0,1,⋯,2N−2
卷积的结果也是一个序列。
现在设有多项式:
F ( x ) = f [ 0 ] + f [ 1 ] x + f [ 2 ] x 2 + ⋯ + f [ N − 1 ] x N − 1 F(x)=f[0]+f[1]x+f[2]x^2+ \cdots +f[N-1]x^{N-1} F(x)=f[0]+f[1]x+f[2]x2+⋯+f[N−1]xN−1
G ( x ) = g [ 0 ] + g [ 1 ] x + g [ 2 ] x 2 + ⋯ + g [ N − 1 ] x N − 1 G(x)=g[0]+g[1]x+g[2]x^2+ \cdots +g[N-1]x^{N-1} G(x)=g[0]+g[1]x+g[2]x2+⋯+g[N−1]xN−1
可以发现两个多项式相乘:
F ( x ) × G ( x ) = f [ 0 ] g [ 0 ] + ( f [ 0 ] g [ 1 ] + f [ 1 ] g [ 0 ] ) x + ( f [ 0 ] g [ 2 ] + f [ 1 ] g [ 1 ] + f [ 2 ] g [ 0 ] ) x 2 + ⋯ = ∑ n = 0 k f [ n ] g [ k − n ] x k , k = 0 , 1 , ⋯ , 2 N − 2 \begin{align*} F(x) \times G(x)=&f[0]g[0]+(f[0]g[1]+f[1]g[0])x+(f[0]g[2]+f[1]g[1]+f[2]g[0])x^2+ \cdots \\ \\ =& \sum_{n=0}^{k}f[n]g[k-n]x^k \,\,,\,\, k=0,1, \cdots ,2N-2 \end{align*} F(x)×G(x)==f[0]g[0]+(f[0]g[1]+f[1]g[0])x+(f[0]g[2]+f[1]g[1]+f[2]g[0])x2+⋯n=0∑kf[n]g[k−n]xk,k=0,1,⋯,2N−2
即多项式相乘后的系数序列是原来两个多项式系数序列的卷积。
[!example]-
F ( x ) = 1 + 0 x + x 2 , f = [ 1 , 0 , 1 ] G ( x ) = 7 + 2 x + 0 x 2 , g = [ 7 , 2 , 0 ] \begin{align*} F(x)=&1+0x+x^2 \,\,,\,\, f=[1,0,1]\\ \\ G(x)=&7+2x+0x^2 \,\,,\,\, g = [7,2,0] \end{align*} F(x)=G(x)=1+0x+x2,f=[1,0,1]7+2x+0x2,g=[7,2,0]
( F × G ) ( x ) = 7 + 2 x + 7 x 2 + 2 x 3 + 0 x 4 , f ∗ g = [ 7 , 2 , 7 , 2 , 0 ] \begin{align*} (F \times G)(x)=7+2x+7x^2+2x^3+0x^4 \,\,,\,\, f*g=[7,2,7,2,0] \end{align*} (F×G)(x)=7+2x+7x2+2x3+0x4,f∗g=[7,2,7,2,0]
1.2.2 多项式与DFT
对于多项式的系数序列表示:
F ( x ) = f [ 0 ] + f [ 1 ] x + f [ 2 ] x 2 + ⋯ + f [ N − 1 ] x N − 1 F(x)=f[0]+f[1]x+f[2]x^2+ \cdots +f[N-1]x^{N-1} F(x)=f[0]+f[1]x+f[2]x2+⋯+f[N−1]xN−1
如果令
x = e − j ω T x=e^{-j \omega T} x=e−jωT
则
F ( x ) = ∑ n = 0 N − 1 f [ n ] e − j ω n T = DTFT F ˉ ( j ω ) \begin{align*} F(x)=&\sum_{n=0}^{ N-1} f[n]e^{-j \omega nT} \stackrel{\text{ DTFT }}{=}\bar F(j \omega ) \end{align*} F(x)=n=0∑N−1f[n]e−jωnT= DTFT Fˉ(jω)
所以使用系数序列表示的多项式,相当于系数序列的离散时间傅里叶变换(DTFT)。
而根据多项式插值定理, N − 1 {N-1} N−1 阶多项式可以被 N {N} N 个点唯一确定,所以 N − 1 {N-1} N−1 阶多项式除了通过系数序列表示,还可以通过多项式上的 N {N} N 个点来表示。即多项式可以表示成
F ( x ) = ∑ n = 0 N − 1 f [ n ] e − j 2 π N k n = DFT F ˉ [ k ] \begin{align*} F(x)=\sum_{n=0}^{ N-1} f[n]e^{-j \frac{\large 2\pi}{\large N} kn} \stackrel{\text{ DFT }}{=} \bar F[k] \end{align*} F(x)=n=0∑N−1f[n]e−jN2πkn= DFT Fˉ[k]
x = e − j ω T = e − j ( 2 π N T ) k T = e − j 2 π N k , k = 0 , 1 , ⋯ , N − 1 x=e^{-j \omega T}=e^{-j(\frac{\large 2\pi}{\large NT})kT}=e^{-j\frac{\large 2\pi}{\large N}k}\,\,,\,\,k=0,1, \cdots ,N-1 x=e−jωT=e−j(NT2π)kT=e−jN2πk,k=0,1,⋯,N−1
所以使用 N {N} N 个点来表示的多项式,相当于系数序列的DFT。结合多项式乘法来看,系数序列的卷积为系数序列傅里叶变换后的乘积,符合傅里叶变换的卷积性质。
1.2.3 多项式乘法与FFT
对使用 N {N} N 个点表示的多项式,多项式的乘积会变得相对简单,因为我们可以快速确定新的多项式上的 N {N} N 个点。
( x i , F ( x i ) × G ( x i ) ) 或 ( k , F [ k ] × G [ k ] ) (x_i,F(x_i) \times G(x_i)) \,\,\, 或 \,\,\, (k,F[k] \times G[k]) (xi,F(xi)×G(xi))或(k,F[k]×G[k])
得到的是多项式乘积的点值表示,对其进行反FFT,即可得到多项式乘积的系数表示。
由于 N {N} N 个点只能确定 N − 1 {N-1} N−1 次多项式,在计算多项式乘法时,我们需要对多项式进行补 0 {0} 0 ,如果要用FFT,需要补成 2 {2} 2 的整数次幂长度。
[!example]-
F ( x ) = 1 + 2 x + 3 x 2 + 4 x 3 G ( x ) = 2 + 3 x + 4 x 2 + 5 x 3 \begin{align*} F(x)=&1+2x+3x^2+4x^3\\ G(x)=&2+3x+4x^2+5x^3 \end{align*} F(x)=G(x)=1+2x+3x2+4x32+3x+4x2+5x3
f : [ 1 , 2 , 3 , 4 , 0 , 0 , 0 , 0 ] g : [ 2 , 3 , 4 , 5 , 0 , 0 , 0 , 0 ] \begin{align*} f:[1,2,3,4,0,0,0,0]\\ g:[2,3,4,5,0,0,0,0] \end{align*} f:[1,2,3,4,0,0,0,0]g:[2,3,4,5,0,0,0,0]
F [ k ] = FFT [ 10 , − 0.4142 − 7.2426 j , − 2 + 2 j , 2.4142 − 1.2426 j , − 2 , 2.4142 + 1.2426 j , − 2 − 2 j , − 0.4142 + 7.2426 j ] F[k] \stackrel{\text{ FFT }}{=} [10,-0.4142-7.2426j,-2+2j,2.4142-1.2426j,-2,2.4142+1.2426j,-2-2j,-0.4142+7.2426j] F[k]= FFT [10,−0.4142−7.2426j,−2+2j,2.4142−1.2426j,−2,2.4142+1.2426j,−2−2j,−0.4142+7.2426j]
G [ k ] = FFT [ 14 , 0.5858 − 9.6569 j , − 2 + 2 j , 3.4142 − 1.6569 j , − 2 , 3.4142 + 1.6569 j , − 2 − 2 j , 0.5858 + 9.6569 j ] G[k] \stackrel{\text{ FFT }}{=} [14,0.5858-9.6569j,-2+2j,3.4142-1.6569j,-2,3.4142+1.6569j,-2-2j,0.5858+9.6569j] G[k]= FFT [14,0.5858−9.6569j,−2+2j,3.4142−1.6569j,−2,3.4142+1.6569j,−2−2j,0.5858+9.6569j]
f ∗ g = IFFT ( F × G ) = [ 2 , 7 , 16 , 30 , 34 , 31 , 20 , 0 ] f*g = \text{IFFT}(F \times G)=[2,7,16,30,34,31,20,0] f∗g=IFFT(F×G)=[2,7,16,30,34,31,20,0]
∴ F ( x ) × G ( x ) = 2 + 7 x + 16 x 2 + 30 x 3 + 34 x 4 + 31 x 5 + 20 x 6 \therefore F(x) \times G(x)=2+7x+16x^2+30x^3+34x^4+31x^5+20x^6 ∴F(x)×G(x)=2+7x+16x2+30x3+34x4+31x5+20x6clc;clear f = [1 2 3 4 0 0 0 0]; F = fft(f) g = [2 3 4 5 0 0 0 0]; G = fft(g) T = F.*G ifft(T) syms x F1 = 1+2*x+3*x^2+4*x^3; G1 = 2+3*x+4*x^2+5*x^3; T1 = F1*G1; collect(T1,x)