【C++】哈希表模拟实现
文章目录
-
- unordered_map 和 unordered_set
- HashTable概念
- CloseHashTable框架
-
- insert()模拟实现
- Find()模拟实现
- Erase()模拟实现
- LinkhashTable框架详解
-
- Insert()模拟实现
- Find()模拟实现
- Erase()模拟实现
- 源码
-
- LinkHash.h
- CloseHash.h
unordered_map 和 unordered_set
在C++98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到 log(N),即最差情况下
需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行很少的比较次
数就能够将元素找到,因此在C++11中,STL又提供了4个unordered系列的关联式容器,这四个容器与红黑
树结构的关联式容器使用方式基本类似,只是其底层结构不同,本文中只对unordered_map和
unordered_set进行介绍,unordered_multimap和unordered_multiset
其底层实现是哈希表,我们接下来就要对哈希表进行学习
HashTable概念
哈希表的实现有多种多样,不同地方构建使用的方法也并不相同,接下来我们将对两种实现方法进行学习
CloseHashTable框架
概念:闭散列哈希表
底层为一个vector存储节点指针,通过对key进行处理,将各个节点的指针存储到vector中。查找时对key进行操作来判断节点位置,进而找到节点

以上即是哈希表的设计思路
但是我们很快就可以发现,一旦出现一个newkey % v.size() 也等于1的话,在vector中索引为1位置已经有值,那么其将插入在哪里呢? 以上这个问题叫做哈希冲突
哈希冲突的解决办法
闭散列哈希表:
1.线性探测:插入在原应该插入位置的后面一个位置,若这个位置还被占了,则继续向后走,直到找到空位
2.二次线性探测:若位置被占,则向后增加1, 4, 9, 16,然后进行取模,直到找到空位

可以看到线性探测中格子都堆在一起,若数据较多,index需要++多次,不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低
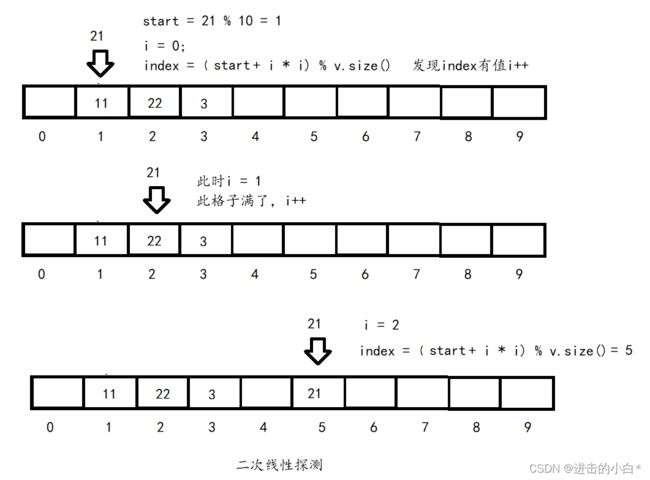
二次线性探测方法每次加上i * i, 让数据较为分散的插入,查找时使用 i * i提高了查找效率。但是如果数据过多,则index,因为i*i并不确定,可能要绕表多次,效率较低,所以当可用数据/容量较高时就要进行扩容,空间利用效率很低。
可用数据/容量 叫做负载因子,线性探测的负载因子一般超过0.7时就要扩容,二次线性探测的负载因子一般超过0.5就要扩容。
可以看到闭散列的方法对空间浪费很大,并且数据较多时搜索效率并不是很高,适用于数据较为随机,并且数量较少的情况
框架
enum Status { EXIST, EMPTY, DELETE };
template<class K, class V>
struct HashData
{
HashData()
:_kv(make_pair(K(), V()))
, _status(EMPTY)
{}
pair<K, V> _kv;
Status _status;
};
template<class K, class V, class HashFunc = Hash<K>>
class HashTable
{
public:
bool insert(const pair<K, V>& kv);
bool Erase(const K& key);
HashData<K, V>* Find(const K& key);
private:
vector<HashData<K, V>> _tables;
size_t _n = 0;
};
这里有两点需要解释一下
1.枚举类型 Status
在我们实际使用哈希表的过程中,若一段连续的数据中被删掉了一个数据,那我们想要查找一个key,而这个节点的指针在删除节点的后面,我们该怎么查找呢?

我们可以看到31在22节点的后面,此时索引为2的节点指针为空。那么到了这个格子是否还应该向后查找?若后面没有31就需要遍历全表判断其是否存在,若使用二次探测则一直找不到可能要陷入死循环。所以我们给每个Node设置一个状态,这个状态反应了这个数据中节点是否存在,还是不存在,还是已经被删除。这样删除节点我们只需要将其状态置为删除就可以了。而遍历走到的格子状态为空就停下

2.模板参数HashFunc
哈希表是需要存储pair
template<class T>
struct Hash
{
size_t operator()(const T& key) { return key; }
};
template<>
struct Hash<string> {
size_t operator()(const string& key) {
int ret = 0;
for (auto ch : key) {
ret += ch;
ret *= 31;
}
return ret;
}
};
正常情况下直接返回key,但是若不能直接取余时对模板进行偏特化。如string,我们取出其每一个字符的将其相加得到一个值进行返回,这样每一个字符串都可以得到一个属于自己的整形key进行比较
insert()模拟实现
template<class K, class V, class Hash>
bool HashTable<K, V, Hash>::insert(const pair<K, V>& kv)
{
if (!_tables.empty() && Find(kv.first))
{
return false;
}
if (_tables.empty() || _n * 10 / _tables.size() >= 7)
{
//扩容
size_t newSize = _tables.size() == 0 ? 10 : 2 * _tables.size();
HashTable<K, V, Hash> newHT;
//将新表的vector进行扩容
newHT._tables.resize(newSize);
//将有效数据个数进行交换
newHT._n = _n;
//将所有的节点重新映射
for (size_t i = 0; i < _tables.size(); i++)
{
if (_tables[i]._status == EXIST)
{
newHT.insert(_tables[i]._kv);
}
}
//交换两个vector
_tables.swap(newHT._tables);
}
Hash hs;
size_t start = hs(kv.first) % _tables.size();
size_t i = 0;
size_t index = start + i;
while (_tables[index]._status == EXIST)
{
++i;
index = (start + i) % _tables.size();
}
_tables[index]._kv = kv;
_tables[index]._status = EXIST;
_n++;
return true;
}
insert函数的插入逻辑在上文已经讲过了,非常简单。但是还有一个重点就是扩容
重新映射 : 一旦扩容那么_tables.size() 必然会发生变化,那么其中数据的映射方式必然会发生改变 比如本来为14的节点是处于索引为4的格子中,但是而被扩容后,其应该处于索引为14的格子里。
因为HashTable的底层是一个vector,现在我们已经写好了一个插入函数,我们可以创建一个新的HashTable对其vector扩容,然后通过遍历原vector中的每一个节点,将其重新映射到新表中,因为新表的容量比旧表大,所以负载因子并不会超,然后通过vector的swap函数将两个表的vector进行交换,这样我们就得到了新的哈希表
Find()模拟实现
template<class K, class V, class Hash>
HashData<K, V>* HashTable<K, V, Hash>::Find(const K& key)
{
Hash hs;
size_t start = hs(key) % _tables.size();
size_t i = 0;
size_t index = start;
while (_tables[index]._status != EMPTY)
{
if (_tables[index]._status == EXIST && _tables[index]._kv.first == key)
{
return &_tables[index];
}
++i;
index = start + i;
}
return nullptr;
}
直接对key进行操作,向后查找到空的位置,若找到则返回节点指针,若找不到则返回空。
注意:因为Erase时我们只改变状态,所以并不能遇到相同的key就返回,还需要检验这个节点的状态是否为EXIST,若为DELET则还是应该返回空
Erase()模拟实现
template<class K, class V, class Hash>
bool HashTable<K, V, Hash>::Erase(const K& key)
{
HashData<K, V>* ret = Find(key);
if (ret)
{
ret->_status = DELETE;
return true;
}
else
return false;
}
若存在则直接改一下状态
LinkhashTable框架详解
概念:开散列哈希表 (拉链法实现)
一个vector,每一个节点下面都可以挂一个单链,每一条单链表我们称之为一个哈希桶,以下即是开散列哈希表的示意图

通过最直观的观察,我们就可以发现,相比较与闭散列开散列更有条理,key经处理后的不同组数据可以很好的被分类。将key处理后直接可以找到位子进行头插,而查找次数最多也就等于桶的高度。
所以在开散列中的效率主要取决于桶的高度,这个我们可以通过控制平衡因子来进行调整。在大部分场景中当平衡因子为1时进行扩容。
效率分析:在开散列哈希表中平衡因子最大为一,平均一下每一个桶的高度仅有一层,只需要进行一次查找,就算出现分布不均的情况,想必查找次数也并不会太多,在对随机数的处理上有很大的优势。相比于最大红黑树树深度次的查找相比,效率还是高了不少
框架
template<class K, class V>
struct HashNode
{
HashNode(const pair<K, V>& kv)
:_kv(kv)
, _next(nullptr)
{}
pair<K, V> _kv;
HashNode<K, V>* _next;
};
template<class K, class V, class HashFunc = Hash<K>>
class HashTable
{
typedef HashNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv);
Node* Find(const K& key);
bool Erase(const K& key);
private:
vector<Node*> _tables;
size_t _n = 0;
};
Insert()模拟实现
template<class K, class V, class Hash>
bool HashTable<K, V, Hash>::Insert(const pair<K, V>& kv)
{
if (!_tables.empty() && Find(kv.first))
return false;
Hash hs;
if (_n >= _tables.size())
{
//扩容
size_t newSize = _tables.size() == 0 ? 10 : 2 * _tables.size();
vector<Node*> newTables;
newTables.resize(newSize);
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t index = hs(cur->_kv.first) % _tables.size();
cur->_next = newTables[index];
newTables[index] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
size_t index = hs(kv.first) % _tables.size();
Node* NewNode = new Node(kv);
NewNode->_next = _tables[index];
_tables[index] = NewNode;
++_n;
return true;
}
开散列的insert非常简单,只需要头插就可以了。
其扩容我们使用创建一个新的vector,然后遍历节点将其链接到新的vector。
此处为什么不能像上文一样创建一个新的表然后复用插入呢?因为在这个地方每一个节点并非开好的而是new出来的,若采用上面的方法就要对所有节点进行深拷贝,然后插入到新表中还要释放旧表的节点。严重影响效率,不如改变节点的链接方式,将其直接插入到新的哈希桶上
Find()模拟实现
template<class K, class V, class Hash>
HashNode<K, V>* HashTable<K, V, Hash>::Find(const K& key)
{
if (_tables.empty())
return nullptr;
Hash hs;
size_t index = hs(key) % _tables.size();
Node* start = _tables[index];
while (start && start->_kv.first != key)
{
start = start->_next;
}
return start;
}
Erase()模拟实现
template<class K, class V, class Hash>
bool HashTable<K, V, Hash>::Erase(const K& key)
{
Hash hs;
size_t index = hs(key) % _tables.size();
Node* cur = _tables[index];
Node* prev = nullptr;
while (cur && cur->_kv.first != key)
{
prev = cur;
cur = cur->_next;
}
if (cur == nullptr)
return false;
else if (prev == nullptr)
{
Node* next = cur->_next;
_tables[index] = next;
delete cur;
cur = nullptr;
return true;
}
else
{
prev->_next = cur->_next;
delete cur;
cur = nullptr;
return true;
}
}
可以观察到Erase并没有复用Find函数,这是因为单链表的删除需要保存其前一个结点,单纯一个结点是不够的。而删除也有几种情况
1.输入的key结点不存在
2.指定的结点在哈希桶的头部/中部/尾部
具体实现还是比较简单的,若有疑问看代码就好了,就不展开说了
下一节我们将对开散列哈希表进行封装成 unordered_map和 unordered_set,并为其添加迭代器,最后我将源码放在最后,供大家观看,测试
源码
LinkHash.h
#pragma once
#include CloseHash.h
#pragma once
#include