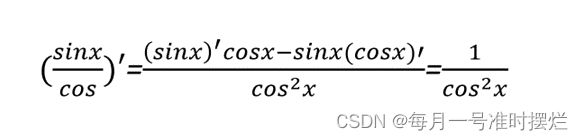利用MATLAB进行求导

导数是微积分中的一个重要的概念，又称为导函数值。在数学中，我们经常会利用导数来求切线、极值、拐点、渐近线等。在解决数学问题中，经常需要用到导数。MATLAB中提供了diff函数进行求导。本文对于MATLAB的求导操作进行简单介绍。

1、求导的定义

求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。本段定义来自百度百科(求导的定义)

2、diff函数

在MATLAB中提供了diff函数用于导数的求导，其中diff函数提供了四种调用方式。

（1）diff(y)：这种调用方式没有指明需要求导的自变量以及导数的阶层数目，一般情况下，是对默认的变量进行一次的求导。

例如，在数学学习中，我们会知道一些比较常用的求导的公式有：

 下面利用MATLAB对其进行验证：

syms x u a
y1=diff(x^u,x)
y2=diff(exp(x))
y3=diff(log(x))
y4=diff(sin(x))
y5=diff(cos(x))
y6=diff(a^x,x)
y7=diff(log(x)/log(a),x)

（注：因为在MALTAB中仅有以自然数e、2和10为底的对数公式，这里转换为log(x)/log(a)的形式）。

运行结果如下所示：

y1 = 
    u*x^(u - 1)
y2 =
    exp(x)
y3 =
    1/x
y4 =
    cos(x)
y5 =
    -sin(x)
y6 =
    a^x*log(a)
y7 =
    1/(x*log(a))
 

通过使用MATLAB代码对于上面的公式进行验证，可以看出MATLAB所计算的结果与公式相同。

在学习导数的时候，我们会学习到导数的乘法与除法的运算法则。

其中导数的乘法运算法则如下所示：

 导数的除法的运算法则如下所示：

 下面利用MATLAB代码对其进行验证，例如下面这个式子对其进行求导操作：

利用MATLAB代码对其进行验证得：

syms x
y=x*exp(x);
diff(y)

运行结果如下所示：

ans =
    exp(x) + x*exp(x)

可以看出结果符合乘法的运算法则。

下面对于除法的运算法则进行验证：

syms x
y=exp(x)/x;
diff(y)

运行结果如下所示：

ans =
    exp(x)/x - exp(x)/x^2

通过MATLAB所输出的结果看出符合除法的运算法则。

下面我们可以对于tan(x)的导数进行验证，tanx转换为sinx/cosx的形式，利用除法的运算法则可以对其进行计算：

syms x
y=sin(x)/cos(x);
diff(y)

运行结果如下所示：

ans =
    sin(x)^2/cos(x)^2 + 1
 

对于MATLAB所计算的结果进行验证：

 而对tanx进行求导的结果如下所示：

 通过对比可以看出MATLAB所求结果正确。

（2）当符号表达式中涉及到了多变量时，diff函数可以指定对于特定符号变量进行求导，调用格式为diff(y,'x')。其中diff(y,'x'):假设需要对其进行求导的变量是x，因为没有说明求导的阶数，这种情况下，MATLAB默认对其进行一阶求导。

例如对于下面的公式进行求导：

 对下面的式子进行求导：

syms x a b c
y=a*x^3+b*x^2+x+c;
diff(y,'x')

运行结果如下所示：

ans =
    3*a*x^2 + 2*b*x + 1

通过上面的例子可以看到，当存在多个符号变量的时候，diff函数可以指定特定的自变量对其进行求导。

（3）另外一种调用方式是指定特定的阶数，未说明对其求导的自变量，调用方式是diff(y,n)，其中对于MATLAB指定的自变量求其n阶导数。

例如同样对下面的公式进行求导：

 MATLAB代码如下所示：

syms x a b c
y=x^3+2*x^2+4*x+6;
diff(y,2)

运行结果如下所示：

ans =
    6*x + 4

（4）最后一种调用方式是对其进行求导的自变量、求导的阶数都进行说明，该方式的调用格式为diff(y,‘x’,n)：该调用方式是以对于自变量x求其n阶导数。

例如，对于下面的式子的x变量求其二阶导数：

 MATLAB代码如下所示：

syms x
y=(x+1)*log(x)-x^2+x+1;
diff(y,'x',2)

运行结果如下所示：

ans =
    2/x - (x + 1)/x^2 - 2

3、利用MATLAB对于复杂的公式求导

通过使用MATLAB对于一些复杂的公式进行求导，方便我们操作。下面对其较为困难的公式进行求导，下面举几个例子：

 MATLAB代码如下所示：

syms x 
y1=diff(sqrt(x)*sin(x),'x',1)
y2=diff(1/((3*x-1)^2),'x',1)
y3=diff(cos(sin(x)),'x',1)

运行结果如下所示：

y1 = 
    x^(1/2)*cos(x) + sin(x)/(2*x^(1/2))
y2 =
    -6/(3*x - 1)^3
y3 =
    -sin(sin(x))*cos(x)

通过运行的结果可以看出，在MATLAB中对于较复杂的符号表达式都可以进行求导操作。