数据结构：Trie树(字典树)

1.何为Trie树

     Trie树,又叫字典树、前缀树，是用来高效存储和查询字符串的数据结构，是一种多叉树

 

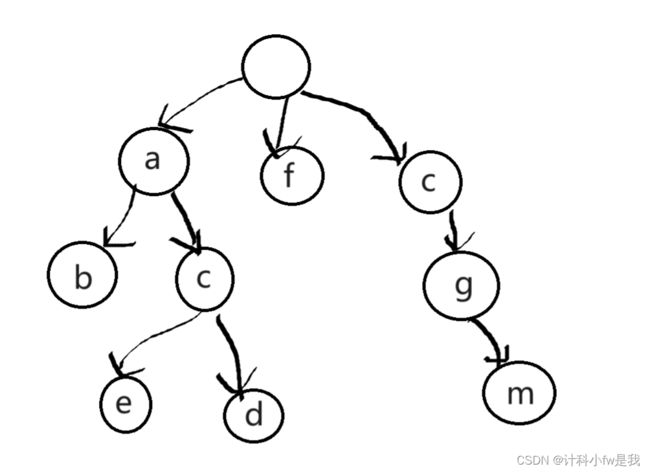
     上图就是一棵Trie树，表示了字符串的集合{"f","ab","ace","acd","cgm"}，一棵Trie树应该是这样的：

1.根节点不存储字符，除此之外每一个子节点都有一个字符
2.从根节点到某一个结点连起来的路径就是该节点对应的字符串
3.每个节点的子节点存储的字符各不相同
4.Trie树不一定是二叉树,它是一种多叉树结构

2.Trie树的实现

     Trie树我们选择用二维数组来模拟实现，首先定义一个son数组，为了知道每个字符串是否存在，我们在最后的每个节点处做了标记，定义一个cnt[p]数组来记录，最后再定义一个idx下标，来表示每个节点

const int N=100010;
int son[N][26],cnt[p],idx;
//son[][]存储树中每个节点的子节点
//cnt[]存储以每个节点结尾的单词数量

     初始时p=0,idx=0,p=0表示此时Trie树为空，p在这里就相当于一个指针；而这里的son数组有两个维度，其中N是代表现在所处的节点位置，而后面的26则是代表当前所在节点的子节点都有26个字母的哪些字母，idx是下标，例如son[0] [0]表示当前在根节点上，它有一个子节点，其中存储了字符a。

      下面就是Trie树的两种基本操作，如果上面看得不是很懂，下面结合实例来进一步解释

2.1 Trie树的插入

void insert(char* str)
{
   int p=0;
   for(int i=0;str[i];i++}//因为字符串是以'\0'结尾的，所以我们可以用str[i]是否为'\0'作为循环的判断条件
 {
   int u=str[i]-'a';
   if(!son[p][u])son[p][u]=++idx;
   p=son[p][u];
 }
   cnt[p]++;
}

      看起来是不是很简单，如何来理解呢？

      假如我们要插入字符串ab，此时树是空的，所以p和idx等于0，首先我们计算出每个字符和a的差值，便于数组的存储，然后字符a和a的差值为0，所以u=0；

      接着我们就要找是否存在根节点的子节点，这个子节点存储了字符a，很显然是没有的，所以我们就要插入字符a，就是son[0][0]=++idx，son[0][0]就表示0这个下标为0的根节点有一个子节点，存储字符a，这个子节点的下标为1；

      然后就令p这个指针指向这个子节点，即p=son[0][0]=1；

      插入字符b的过程，计算b和字符a的差值为1，u=1；此时p=1，指向a这个节点，判断son[1][1]是否存在，发现没有这个子节点，进行插入，即son[1][1]=++idx=2，表示下标为1的节点a有一个子节点，存储字符b，这个子节点的下标为2。

      然后就令p指针指向这个子节点，即p=son[1][1]=2；

     此时插入结束，我们用计数来表示是否存在，令cnt[2]++，表示从根节点到下标2的这个节点的路径所存储的字符串是存在的。

      如果我们再插入ace字符串，又是什么样的？

      此时上一个循环结束，插入了第一个字符串，令p指针=0，重新指向根节点，我们再次计算a和字符a的差值，u=0，此时再判断son[0][0]，发现是存在的，所以我们直接令p=son[0][0]。

      接着计算c与a的差值为2，发现son[1][2]不存在，那我们就插入，令son[1][2]=++idx=3，再令p指向这个节点；继续计算e与a的差值为4，发现son[3][4]也不存在，继续插入，令son[3][4]=++idx=4，令p指向这个节点；这时候插入结束，我们令cnt[4]++，表示从根节点到下标为4的节点的路径存储的字符串是存在的！

      继续插入字符串f，cgm，步骤是一样的，最后就是这样：

2.2 Trie树的查询

     Trie树查询的代码和插入是很像的

int query(char* str)
{
   int p=0;
   for(int i=0;str[i];i++)
   {
     int u=str[i]-'a';
     if(!son[p][u])return 0;
     p=son[p][u];
   }
    return cnt[p];
}

     是不是和插入的代码很像，不过就是当我们发现没有某个字符时，我们就可以直接判定不存在这个字符串，返回0就好了；如果存在，最后返回cnt[p]。

3.Trie树例题

字符串统计

     本题选自Acwing平台

#include
using namespace std;
const int N=100010;
int son[N][26],cnt[N],idx;
char str[N];
void Insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}
int query(char str[])
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}
int main()
{
    
  int n;
  cin>>n;
  while(n--)
  {
      char op[2];
      scanf("%s%s",op,str);
      if(op[0]=='I')Insert(str);
      else printf("%d\n",query(str));
  }
    return 0;
}

 

       Trie树有个明显的提示，它一般用来存储小写或大写英文字母、数字，而不会存储其他字符，所以当题目说字符串仅包含小写英文字母时，我们就要考虑用Trie树了。