【C/C++笔试练习】sort排序、STL容器、vector的特性、一级容器、迭代器失效、异常捕获、动态转换、统计每个月兔子的总数、字符串通配符

C/C++笔试练习

选择部分

（1）sort是不稳定排序

  以下关于STL的描述中，（）是错的

  A. STL容器是线程不安全的
  B. 当容量不够时，STL的一个典型实现是vector内部内存扩展方式为翻倍
  C. std::sort是稳定排序
  D. std::bitset不是一个STL容器

  答案：C

  A.STL容器并不是线程安全的。 如果在多个线程中同时修改同一个STL容器，可能会导致未定义的行为。为了在多线程环境中安全地使用STL，需要处理同步，或者使用某些线程安全的STL变体。

  B.std::vector 的一个常见实现策略是当其容量不足以容纳更多元素时，会按2倍扩容（Linux下）或者1.5扩容（VS下）。 这样做的目的是为了减少重新分配和复制元素的次数，从而提高性能。

  C.std::sort 不是稳定的。sort的底层是插入排序和快速排序结合的算法，稳定排序意味着相等的元素在排序后保持其原始顺序，快排不满足稳定排序的特点。

  D.std::bitset是一个位集合，它只能存储二进制位， 所以不能叫做容器。

  

（2）存放即有序的STL容器

  以下STL的容器存放的数据，哪个肯定是排好序的（）

  A. vector
  B. deque
  C. list
  D. map

  答案：D

  map的底层为平衡搜索树(红黑树)，会默认根据数据的键对值排序。

  

（3）连续储存的STL容器

  以下哪种STL容器中的对象是连续存储的（）

  A. list
  B. vector
  C. map
  D. set

  答案：B

  list是一个双向链表，它的元素是通过链表节点连续存储的，但这种连续不是物理内存上的连续。vector是一个动态数组，它的元素在物理内存中是连续存储的。

  map是一个关联容器，它使用红黑树（或某些其他平衡二叉搜索树）来存储元素。元素在物理内存中不是连续存储的。set和map 类似。

  

（4）vector的特性

  STL中的哪种结构在增加成员时可能会引起原有成员的存储位置发生改变（）

  A. map
  B. set
  C. list
  D. vector

  答案：D

  list是一个双向链表。在链表中增加一个新元素时，不会改变已有元素的存储位置。vector是一个动态数组。当向vector 中添加一个新元素时，它可能需要重新分配内存并移动所有元素到新的内 存位置，从而改变它们的存储位置。

  map是一个关联容器，它使用红黑树（或某些其他平衡二叉搜索树）来存储元素。在增加一个新元素时，可能会引起树结构的调整，但不会改变已有元素的存储位置。set和map 类似。

  

（5）一级容器

  STL中的一级容器有:

  A. vector, deque, list, set, multiset, map, multimap.
  B. 序列容器，关联容器，容器适配器
  C. set, multiset, map, multimap.
  D. vector, deque, list.

  答案：D

  一级容器：数据类型不能是组合类型，只能是内置类型的容器。
  如：vector； vector>；

  注意：pair，key-value值对结构也是组合类型：map;

  所以属于STL一级容器的是vector, deque, list。

  

（6）unordered_map和priority_queue的底层

  STL中的unordered_map和priority_queue使用的底层数据结构分别是什么（）

  A. rbtree,queue
  B. hashtable,heap
  C. rbtree,heap
  D. hashtable,queue

  答案：B

  unordered_map: 使用哈希表（hashtable）作为其底层数据结构。

  priority_queue: 使用堆（heap）作为其底层数据结构。

  

（7）迭代器失效

  下面关于迭代器失效的描述哪个是错误的（）

  A. vector的插入操作不会导致迭代器失效
  B. map的插入操作不会导致迭代器失效
  C. vector的删除操作只会导致指向被删除元素及后面的迭代器失效
  D. map的删除操作只会导致指向被删除元素的迭代器失效

  答案：A

  A. 当在vector中进行插入操作时，迭代器可能失效。特别是当插入发生在容器中间或末尾时，它可能会导致需要重新分配内部存储，从而让指向向量中间元素的迭代器变得无效。

  B.map的插入操作不会使迭代器失效，因为map的内部是平衡树结构。

  C.当从vector中删除一个元素时，指向被删除元素和其后面的元素的迭代器会失效，但是前面的元素不会失效。

  D.map的删除操作只会使指向被删除元素的迭代器失效。

  

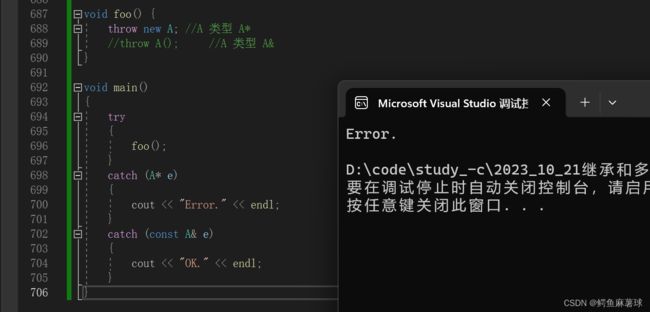
（8）异常捕获

  如何捕获异常可以使得代码通过编译？

class A {
public:
	A(){}
};

void foo(){
	throw new A;
}

  A. catch (A && x)
  B. catch (A * x)
  C. catch (A & x)
  D. 以上都是

  答案：B

  A.catch (A && x)这是一个右值引用捕获，它捕获的是对象（例如new A返回的指针）的移动语义。但是，throw new A;语句抛出一个动态分配的A类型的对象，而不是移动语义。因此，此选项是错误的。

  B. catch (A * x)这是一个指针捕获，它能够捕获动态分配的对象，如new A。这是正确的捕获方式。

  C. catch (A & x)这是一个引用捕获，它通常用于捕获基本数据类型或静态分配的对象。对于动态分配的对象，引用捕获是不适用的，因为它们不能被移动或复制。因此，此选项是错误的。

  

（9）动态转换

  有如下程序段：

#include 
using namespace std;

class A {
public:
	~A() {cout << "~A()";}
};

class B{
public:
	virtual ~B() {cout << "~B()";}
};

class C: public A, public B {
public:
	~C() {cout << "~C()";}
};

int main() {
	C * c = new C;
	B * b1 = dynamic_cast<B *>(c);
	A * a2 = dynamic_cast<A *>(b1);
	delete a2;
}

  则程序输出：

  A. ~C() ~B() ~A()
  B. ~C() ~A() ~B()
  C. A)B)都有可能
  D. 以上都不对

  答案：D

int main() {
	C* c = new C;//1.构造对象C,C是由A,B继承得来的
	B* b1 = dynamic_cast<B*>(c);//2.B类型指针b1动态转换为c,这里没有问题，父类指针指向子类
	A* a2 = dynamic_cast<A*>(b1);//3.A类型指针a2动态转换为B类型的指针b1
	delete a2;//4.释放子类C,但是A类型和B类型没有任何继承关系，导致程序崩溃
}

  

（10）多态的实现

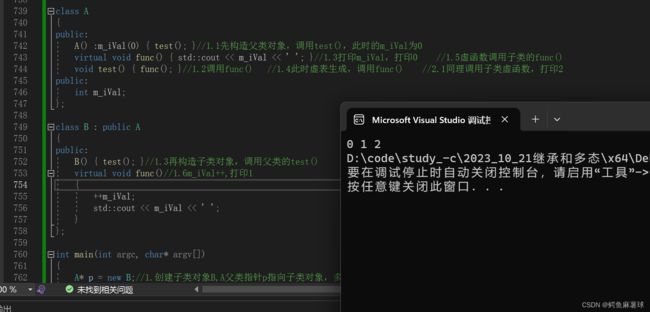
  以下程序输出结果是____

class A
{
public:
	A ():m_iVal(0){test();}
	virtual void func() { std::cout<<m_iVal<<‘ ’;}
	void test(){func();}
public:
	int m_iVal;
};

class B : public A
{
public:
	B(){test();}
	virtual void func()
	{
		++m_iVal;
		std::cout<<m_iVal<<‘ ’;
	}
};

int main(int argc ,char* argv[])
{
	A*p = new B;
	p->test();
	return 0;
}

  A. 1 0
  B. 0 1
  C. 0 1 2
  D. 2 1 0
  E. 不可预期
  F. 以上都不对

  答案：C

class A
{
public:
	A() :m_iVal(0) { test(); }//1.1先构造父类对象，调用test()，此时的m_iVal为0
	virtual void func() { std::cout << m_iVal << ' '; }//1.3打印m_iVal，打印0    					  
													   //1.5虚函数调用子类的func()  
	void test() { func(); }//1.2调用func()   
						   //1.4此时虚表生成，调用func()    
						   //2.1同理调用子类虚函数，打印2
public:
	int m_iVal;
};

class B : public A
{
public:
	B() { test(); }//1.3再构造子类对象，调用父类的test()
	virtual void func()//1.6m_iVal++,打印1
	{
		++m_iVal;
		std::cout << m_iVal << ' ';
	}
};

int main(int argc, char* argv[])
{
	A* p = new B;//1.创建子类对象B,A父类指针p指向子类对象，多态的信号
	p->test();//2.父类指针调用函数test()
	return 0;
}

            

编程题 day18

统计每个月兔子的总数

统计每个月兔子的总数

  解题思路：第n个月的兔子数量由两部分组成，一部分是上个月的兔子f(n-1)，另一部是满足3个月大的兔子，会生一只兔子f(n-2)。所以第n个月兔子总数： f(n) = f(n - 1) + f(n - 2)。本题是在变相考察斐波那契数列。

#include
using namespace std;

/*
//迭代法求解
int Fib(int n)
{
    if(n <= 2)
    return 1;
    int f, f1=1, f2=1;
    for(int i=3; i<=n; ++i)
    {
        f = f1 + f2;
        f1 = f2;
        f2 = f;
    }
    return f;
}
*/

//递归法求解
int Fib(int n) 
{
    if (n <= 2)
        return 1;
    else
        return Fib(n - 1) + Fib(n - 2);
}

int main() 
{
    int month;
    int sum = 0;
    while (cin >> month) 
    {
        sum = Fib(month);
        cout << sum << endl;
    }
    return 0;
}

  

字符串通配符

字符串通配符

  解题思路：本题可以通过递归求解。从前向后一次匹配，遇到相同字符，都向后移动一个字符，如果通配符遇到"?“，则不需匹配，自动跳过一个字符，如果通配符遇到”*"，则可以匹配任意多个字符，包括0个，此时可以有三种选择，1，匹配0个，通配符向后移动一个字符，字符串不动。2，匹配1个，通配符和字符串都向后移动一个字符。3，匹配多个，通配符不动，字符串向后移动一个字符。递归的终止条件：通配符或者字符串遇到’\0’。当他们同时结束。

#include
#include
#include
#include
using namespace std;

bool Match(const string& patter, const string& str, int i, int j)
{
    if(i == patter.size() && j == str.size())
    {   
        return true;
    }
    if(i == patter.size() || j == str.size())
    {
        return false;
    }

    if(patter[i] == '?')
    {
        if(!isdigit(str[j]) && !isalpha(str[j]))
        {
            return false;
        }
        return Match(patter, str, i + 1, j + 1);
    }
    else if(patter[i] == '*')
    {
        while(patter[i] == '*')
        {
            i++;
        }
        i--;

        if(!isdigit(str[j]) && !isalpha(str[j]))
        {
            return Match(patter, str, i + 1, j);
        }
        return Match(patter, str, i + 1, j) //匹配0个
        || Match(patter, str, i + 1, j + 1)//匹配一个
        || Match(patter, str, i, j + 1)//匹配n个
        ;
    }
    else if(tolower(patter[i]) == tolower(str[j]))
    {
        return Match(patter, str, i + 1, j + 1);
    }
    else 
    {
        return false;
    }
}

int main()
{
    string s1;
    getline(cin, s1);
    string s2;
    getline(cin, s2);
    if(Match(s1, s2, 0, 0)) 
        cout<<"true"<<endl;
    else
        cout<<"false"<<endl;
    return 0;
}