Transformer模型中的Attention算法
参考【经典精读】万字长文解读Transformer模型和Attention机制 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/104393915图解Transformer_transformer模型训练准确率曲线图-CSDN博客
Transformer是《Attention is all you need》论文里提出来的新的框架，其就是一个升级版的seq2seq，也是由一个encoder和一个decoder组成的。encoder对输入序列进行编码，decoder对encoder的结果进行解码。但是，encoder和decoder都不用RNN，而且换成了多个attention。
Transformer的核心优势在于：
由于同一个序列的不同位置之间的平行关系，带来了两个重要优势
（1）它在训练时相对序列长度的复杂度是O(1) （实际上还是有一些额外的开销，比如attention里的某些运算复杂度和长度呈线性关系），和先辈RNN的O(N)复杂度比起来是一个重大突破；
（2）做到了真正的双向context融合，在此之前我们只有BiLSTM，但是其本质只是两个单向建模的叠加，而不是Transformer这种彻底的context融合
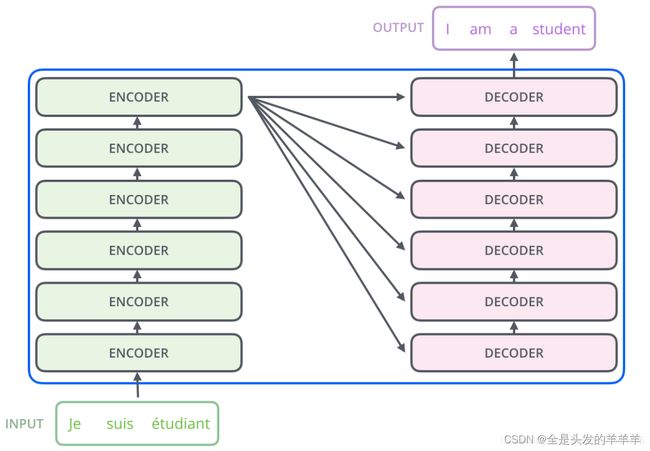
看起来很复杂的结构，其实就是这样一个Encoders和一个Decoders
每个Encoders中分别由6个Encoder组成（论文中是这样配置的）。而每个Decoders中同样也是由6个Decoder组成。
对于Encoders中的每一个Encoder，他们结构都是相同的，但是并不会共享权值。每层Encoder有2个部分组成，如下图：
每个Encoder的输入首先会通过一个self-attention层，通过self-attention层帮助Endcoder在编码单词的过程中查看输入序列中的其他单词。
Self-attention的输出会被传入一个全连接的前馈神经网络，每个encoder的前馈神经网络参数个数都是相同的，但是他们的作用是独立的。
每个Decoder也同样具有这样的层级结构，但是在这之间有一个Attention层，帮助Decoder专注于与输入句子中对应的那个单词
将每个单词编码为一个512维度的向量，我们用上面这张简短的图形来表示这些向量。词嵌入的过程只发生在最底层的Encoder。但是对于所有的Encoder来说，你都可以按下图来理解。输入（一个向量的列表，每个向量的维度为512维，在最底层Encoder作用是词嵌入，其他层就是其前一层的output）。另外这个列表的大小和词向量维度的大小都是可以设置的超参数。一般情况下，它是我们训练数据集中最长的句子的长度。
在每个单词进入Self-Attention层后都会有一个对应的输出。Self-Attention层中的输入和输出是存在依赖关系的，而前馈层则没有依赖，所以在前馈层，我们可以用到并行化来提升速率。
假设下面的句子就是我们需要翻译的输入句：
”The animal didn't cross the street because it was too tired”
这句话中的"it"指的是什么？它指的是“animal”还是“street”？对于人来说，这其实是一个很简单的问题，但是对于一个算法来说，处理这个问题其实并不容易。self attention的出现就是为了解决这个问题，通过self attention，我们能将“it”与“animal”联系起来。
当模型处理单词的时候，self attention层可以通过当前单词去查看其输入序列中的其他单词，以此来寻找编码这个单词更好的线索。
self-attention
这一节我们先介绍如何用向量的方式来计算self attention，然后再来看看它是如何使用矩阵来实现的。
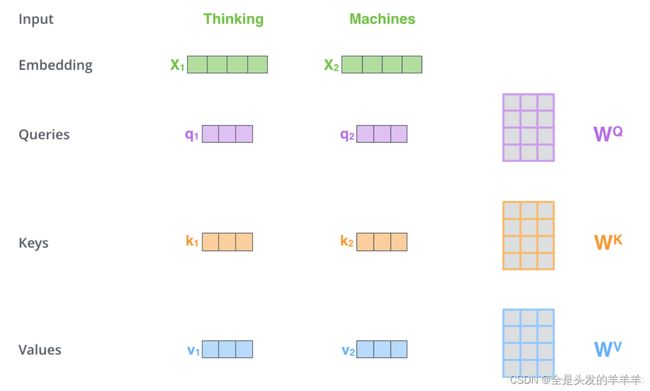
计算self attention的第一步是从每个Encoder的输入向量上创建3个向量（在这个情况下，对每个单词做词嵌入）。所以，对于每个单词，我们创建一个Query向量，一个Key向量和一个Value向量。这些向量是通过词嵌入乘以我们训练过程中创建的3个训练矩阵而产生的。
注意这些新向量的维度比嵌入向量小。我们知道嵌入向量的维度为512，而这里的新向量的维度只有64维。新向量并不是必须小一些，这是网络架构上的选择使得Multi-Headed Attention（大部分）的计算不变。
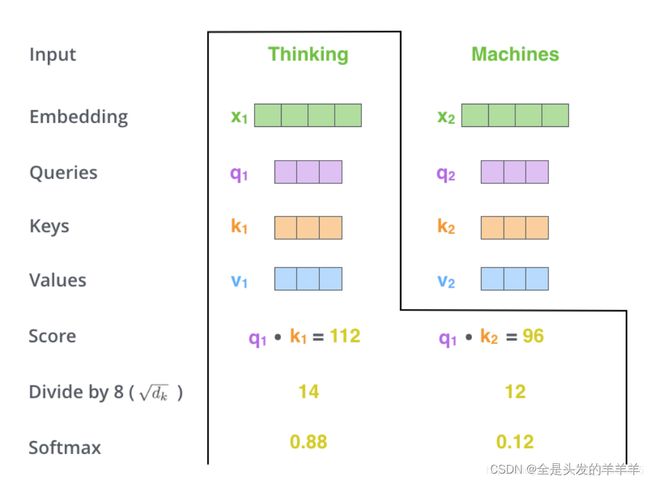
计算self attention的第二步是计算得分。以上图为例，假设我们在计算第一个单词“thinking”的self attention。我们需要根据这个单词对输入句子的每个单词进行评分。当我们在某个位置编码单词时，分数决定了对输入句子的其他单词的关照程度。
通过将query向量和key向量点积来对相应的单词打分。所以，如果我们处理开始位置的的self attention，则第一个分数为
和
的点积，第二个分数为
和
的点积。如下图
第三步和第四步的计算，是将第二部的得分除以8（
）（论文中使用key向量的维度是64维，其平方根=8，这样可以使得训练过程中具有更稳定的梯度。这个并不是唯一值，经验所得）。然后再将得到的输出通过softmax函数标准化，使得最后的列表和为1。
为什么要有缩放因子
?
- 先一句话回答这个问题: 缩放因子的作用是归一化。
- 假设Q , K里的元素的均值为0，方差为1，那么
=
中元素的均值为0，方差为d. 当d变得很大时， A 中的元素的方差也会变得很大，如果 A 中的元素方差很大，那么softmax(A) 的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。总结一下就是softmax(A)的分布会和d有关。因此A 中每一个元素乘上 后，方差又变为1。这使得softmax(A) 的分布“陡峭”程度与d解耦，从而使得训练过程中梯度值保持稳定。
这个softmax的分数决定了当前单词在每个句子中每个单词位置的表示程度。很明显，当前单词对应句子中此单词所在位置的softmax的分数最高，但是，有时候attention机制也能关注到此单词外的其他单词，这很有用。
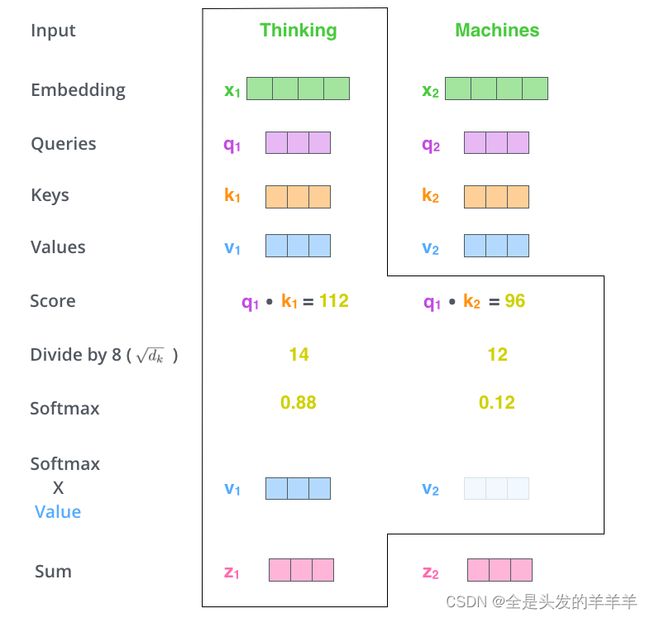
第五步是将每个Value向量乘以softmax后的得分。这里实际上的意义在于保存对当前词的关注度不变的情况下，降低对不相关词的关注。
第六步是 累加加权值的向量。 这会在此位置产生self-attention层的输出（对于第一个单词）。
总结self-attention的计算过程，（单词级别）就是得到一个我们可以放到前馈神经网络的矢量。 然而在实际的实现过程中，该计算会以矩阵的形式完成，以便更快地处理。下面我们来看看Self-Attention的矩阵计算方式。
Matrix Calculation of Self-Attention
第一步是去计算Query，Key和Value矩阵。我们将词嵌入转化成矩阵X中，并将其乘以我们训练的权值矩阵（
,
,
）
X矩阵中的每一行对应于输入句子中的一个单词。 我们看到的X每一行的方框数实际上是词嵌入的维度，图中所示的和论文中是有差距的。X（图中的4个方框论文中为512个）和q / k / v向量（图中的3个方框论文中为64个）
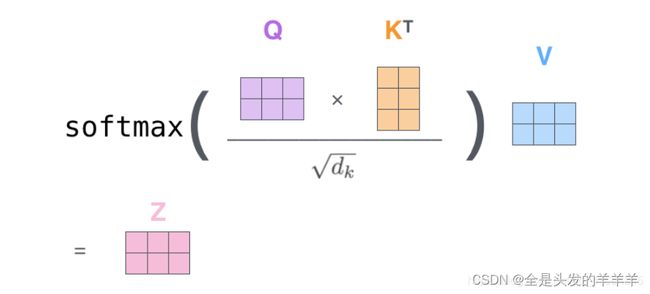
最后，由于我们正在处理矩阵，我们可以在一个公式中浓缩前面步骤2到6来计算self attention层的输出。
使用位置编码表示序列的顺序
到目前为止，模型中缺少的一件事是解释输入序列中单词顺序的方法。
为了解决这个问题，transformer 在每个输入嵌入中添加一个向量。这些向量遵循模型学习的特定模式，这有助于它确定每个单词的位置，或序列中不同单词之间的距离。这里的直觉是，一旦嵌入向量被投影到 Q/K/V 向量中，并且在点积注意力期间，将这些值添加到嵌入向量之间提供了有意义的距离。
为了让模型了解单词的顺序，我们添加了位置编码向量——其值遵循特定的模式。
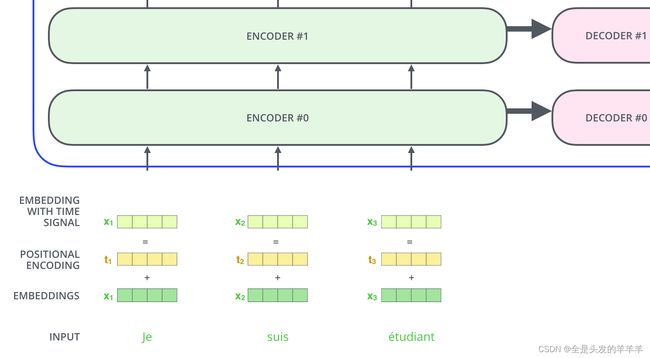
为了让模型捕捉到单词的顺序信息，我们添加位置编码向量信息（POSITIONAL ENCODING）-位置编码向量不需要训练，它有一个规则的产生方式。
如果我们的嵌入维度为4，那么实际上的位置编码就如下图所示：
A real example of positional encoding with a toy embedding size of 4
这种模式可能是什么样子的？
在下图中，每一行对应一个向量的位置编码。因此，第一行是我们添加到输入序列中第一个单词嵌入的向量。每行包含 512 个值，每个值的值介于 1 和 -1 之间。我们对它们进行了颜色编码，因此图案是可见的。
嵌入大小为 512（列）的 20 个单词（行）的位置编码的真实示例。你可以看到它从中心分成两半。这是因为左半部分的值是由一个函数（使用正弦）生成的，而右半部分的值是由另一个函数（使用余弦）生成的。然后将它们连接起来形成每个位置编码向量。
残差
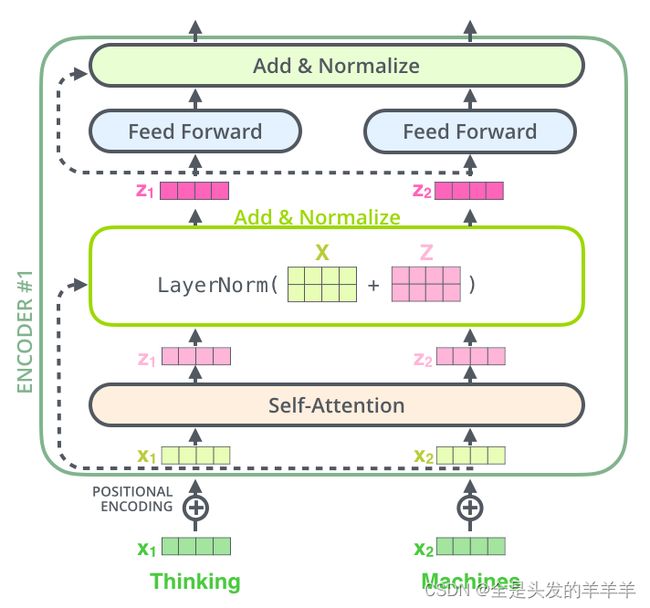
我们还需要在编码器架构中提到一个细节，即每个编码器中的每个子层(self-attention, ffnn) 周围都有一个残余连接，然后是层归一化步骤。
如果我们要可视化与自我注意力相关的向量和层范数操作，它看起来像这样：
Decoder的子层也是同样的，如果我们想做堆叠了2个Encoder和2个Decoder的Transformer，那么它可视化就会如下图所示：
Decoder
编码器首先处理输入序列。然后，顶部编码器的输出被转换为一组注意力向量 K 和 V。每个解码器在其“编码器-解码器注意力”层中使用这些，这有助于解码器专注于输入序列中的适当位置：
以下步骤重复该过程，直到到达一个特殊符号，指示转换器解码器已完成其输出。每个步骤的输出在下一个时间步中被馈送到底部解码器，解码器像编码器一样冒出它们的解码结果。就像我们对编码器输入所做的那样，我们在这些解码器输入中嵌入并添加位置编码，以指示每个单词的位置。
Decoder中的self attention与Encoder的self attention略有不同：
在Decoder中，self attention只关注输出序列中的较早的位置。这是在self attention计算中的softmax步骤之前屏蔽了特征位置（设置为 -inf）来完成的。
“Encoder-Decoder Attention”层的工作方式与"Multi-Headed Self-Attention"一样，只是它从下面的层创建其Query矩阵，并在Encoder堆栈的输出中获取Key和Value的矩阵。
最终的线性层和 Softmax 层
Decoder堆栈输出浮点数向量。我们如何把它变成一个词？这是最后一个线性层的工作，然后是 Softmax 层。
线性层是一个简单的全连接神经网络，它将Decoder堆栈产生的向量投射到一个更大的向量中，称为对数向量。
假设我们的模型知道 10,000 个独特的英语单词（我们模型的“输出词汇表”），这些单词是从其训练数据集中学习到的。这将使对数向量有 10,000 个单元格宽——每个单元格对应一个唯一单词的分数。这就是我们如何解释模型的输出，然后是线性层。
然后，softmax 层将这些分数转换为概率（全部为正数，加起来为 1.0）。选择概率最高的单元格，并生成与其关联的单词作为此时间步的输出。
嵌入大小为 512（列）的 20 个单词（行）的位置编码的真实示例。你可以看到它从中心分成两半。这是因为左半部分的值是由一个函数（使用正弦）生成的，而右半部分的值是由另一个函数（使用余弦）生成的。然后将它们连接起来形成每个位置编码向量。
Recap Of Training
现在我们已经讲解了transformer的训练全过程了，让我们回顾一下。
在训练期间，未经训练的模型将通过如上的流程一步一步计算的。而且因为我们是在对标记的训练数据集进行训练（机器翻译可以看做双语平行语聊），那么我们可以将模型输出与实际的正确答案相比较，来进行反向传播。
为了更好的理解这部分内容，我们假设我们输出的词汇只有（“a”，“am”，“i”，“thanks”，“student”和“
我们模型的输出词汇表是在我们开始训练之前的预处理阶段创建的。
一旦我们定义了输出的词汇表，那么我们就可以使用相同宽度的向量来表示词汇表中的每个单词。称为one-hot编码。例如，我们可以使用下面向量来表示单词“am”：
示例：输出词汇表的独热编码
在此回顾之后，让我们讨论模型的损失函数 - 我们在训练阶段优化的指标，以产生一个经过训练且希望非常准确的模型。
The Loss Function
假设我们正在训练一个模型，比如将“merci”翻译成“thanks”。这意味着我们希望模型计算后的输出为“谢谢”，但由于这种模式还没有接受过训练，所以这种情况不太可能发生。
由于模型的参数（权重）都是随机初始化的，因此（未经训练的）模型会为每个单元格/单词生成具有任意值的概率分布。我们可以将其与实际输出进行比较，然后使用反向传播调整模型的所有权重，使输出更接近所需的输出。
如何比较两种概率分布？我们只是从另一个中减去一个。有关更多详细信息，请查看交叉熵和 Kullback-Leibler 散度。
但请注意，这是一个过于简化的示例。更现实地说，我们将使用一个比一个单词更长的句子。例如，输入：“je suis étudiant”和预期输出：“i am a student”。这真正意味着，我们希望我们的模型连续输出概率分布，其中：
- 每个概率分布都由宽度为 vocab_size 的向量表示（在我们的玩具示例中为 6，但更实际地说是 30,000 或 50,000 等数字）
- 第一个概率分布在与单词“i”关联的单元格中具有最高概率
- 第二个概率分布在与单词“am”关联的单元格中具有最高概率
- 依此类推，直到第五个输出分布指示 '' 符号，该符号也有一个来自 10,000 个元素词汇表的单元格与之关联。
我们将在一个示例句子的训练示例中训练模型的目标概率分布。
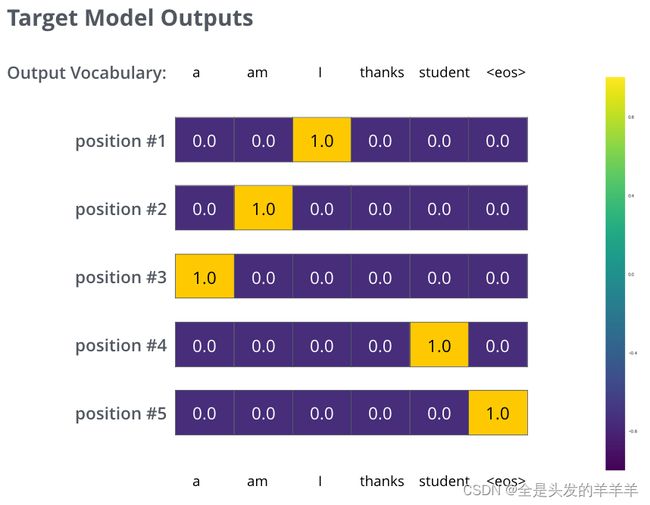
在足够大的数据集上训练模型足够长的时间后，我们希望生成的概率分布如下所示：
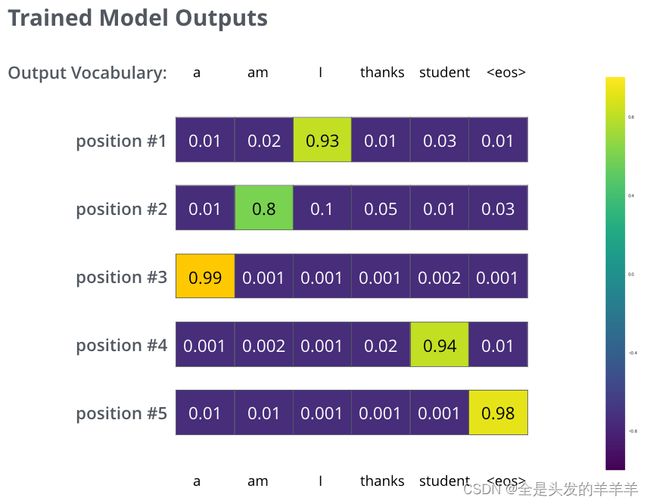希望在训练时，该模型将输出我们期望的正确翻译。当然，这并不是真正表明这句话是否是训练数据集的一部分（参见： 交叉验证）。请注意，每个位置都会获得一点概率，即使它不太可能是该时间步的输出——这是 softmax 的一个非常有用的属性，有助于训练过程。
现在，由于模型一次生成一个输出，我们可以假设模型从该概率分布中选择概率最高的单词并丢弃其余的单词。这是一种方法（称为贪婪解码）。另一种方法是保留前两个单词（例如，“I”和“a”），然后在下一步中运行模型两次：一次假设第一个输出位置是单词“I”，另一个假设第一个输出位置是单词“a”，考虑到位置 #1 和 #2，无论哪个版本产生的误差都较小。我们对位置 #2 和 #3 重复此操作......等。这种方法称为“光束搜索”，在我们的示例中，beam_size是两个（这意味着在任何时候，两个部分假设（未完成的翻译）都保留在内存中），top_beams也是两个（意味着我们将返回两个翻译）。这些都是可以试验的超参数。
- 阅读 Attention Is All You Need 论文、Transformer 博客文章（Transformer：用于语言理解的新型神经网络架构）和 Tensor2Tensor 公告。
- 观看 Łukasz Kaiser 的演讲，了解模型及其细节
- 使用作为 Tensor2Tensor 存储库的一部分提供的 Jupyter Notebook
- 探索 Tensor2Tensor 存储库。
后续工作：
- 用于神经机器翻译的深度可分离卷积
- 一个模型来学习所有模型
- 序列模型的离散自动编码器
- 通过汇总长序列生成维基百科
- 图像转换器
- Transformer 模型的训练技巧
- 具有相对位置表示的自注意力
- 使用离散潜在变量在序列模型中快速解码
- Adafactor：具有亚线性内存成本的自适应学习率