leetcode算法python,C++解题笔记
目录
- 数组
-
- 动态数组的建立C++
- 1.删除排序数组重复项(简单)数组双指针问题
-
- python实现
- C++实现
- 2.买卖股票的最佳时机 II 贪心算法
-
- 贪心算法的框架
- python实现
- 3. 缺失的第一个正数 数组排序 困难
-
- 算法的时间复杂度和空间复杂度
-
- 时间复杂度
- 空间复杂度
- 时空权衡
-
- 暴力枚举
- 辅助哈希表
- 4、数组矩阵原地旋转
-
- python // 整除向小取整
- 数据结构之哈希表
-
- 解题
- 1.哈希表解题
-
- 思路
- 方法:
- 4、给定一个整数数组,判断是否存在重复元素。简单
-
- 思路:
-
- 1、排序:
- 1.1 冒泡排序
- 题解一:类似冒泡排序,超出时间复杂度,用了两个for循环,时间复杂度为O(n^2)
- 1.2 归并排序
- 题解二:归并排序+找相邻元素 通过
- 链表
-
- 单向链表
- 双向链表
- 题目
-
- 初级算法
- 1、删除链表的倒数第N个节点,求解链表长度
- 2、链表的反转
-
- 2.1 双链表双指针求解
- 2.2 栈求解
- 3、合并两个有序链表
- 4、判断回文链表
-
- 进阶 你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
- 5、环形链表
-
- 快慢指针解决
- 队列
- 栈
-
- 动态数组实现栈C++
- 1、每日温度
- 栈和DFS深度优先搜索
-
- 例子一从A节点找到G节点的路径
- 树
-
- 一些概念总结
- 1、简单题:求二叉树的最大深度
- 题解一 深度优先搜索(DFS)
- 题解二 广度优先搜索(BFS)
- 2、平衡二叉搜索数AVL(实现代码未看)
-
- AVL树的性质:
- 题目剑指判断平衡二叉树
-
- 自顶向下
- 自底向上
- 堆
-
- 创建堆
- 插入元素
- 删除堆顶元素
- 获取堆的长度
-
- 应用——堆排序
- 输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
- 图
-
- 一、并查集
-
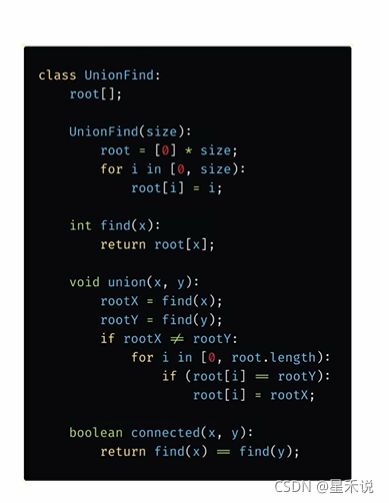
- quick find伪代码:
- quick union
- 题目——力扣 547 省份数量
- 总结
- 按秩合并的并查集
- 基于路径压缩的并查集
- 将秩合并和路径压缩结合♥♥
- 二、图的深度优先搜索
-
- 题目 797. 所有可能的路径
- 三、广度优先搜索
- 算法设计
-
- 动态规划
- 爬楼梯
数组
动态数组的建立C++
// 初始化可变数组
vector<int> array;
// 向尾部添加元素
array.push_back(2);
array.push_back(3);
array.push_back(1);
array.push_back(0);
array.push_back(2);
//初始化size,但每个元素值为默认值
vector<int> abc(10); //初始化了10个默认值为0的元素
//初始化size,并且设置初始值
vector<int> cde(10,1); //初始化了10个值为1的元素
作者:Krahets
链接:https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50e446/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1.删除排序数组重复项(简单)数组双指针问题
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
如:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
python实现
遇到相同元素就删除
class Solution(object):
def removeDuplicates(self, nums):
i=1
for r in range(0,len(nums)-1):
if nums[i]==nums[i-1]:
del nums[i]
i=i-1
i=i+1
return len(nums)
leetcode上看见的比较好的解法
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
for i in range(len(nums) - 1, 0, -1):
if nums[i] == nums[i - 1]:
del nums[i]
return len(nums)
作者:xuanli
链接:https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/x2gy9m/?discussion=GI58ZK
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
C++实现
开始的想法是看到相同的项就用后面的替换,但是这样做超过时间限制了,直接找到不同的数替换到前面即可
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.empty()){
return 0;
}
int index = nums.size();
int sum=1;
int t=1;
for(int i=0;i<index-1;i++){
if(nums[i+1]==nums[i]){
continue;
}
else{
nums[t] = nums[i+1];
t++;
sum++;
}
}
return sum;
}
};
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.empty()){
return 0;
}
int index = nums.size();
int sum=1;
int t=1;
for(int i=0;i<index-1;i++){
if(nums[i+1]==nums[i]){
continue;
}
else{
nums[t] = nums[i+1];
t++;
sum++;
}
}
return sum;
}
};
作者:TNT_tr
链接:https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/x2gy9m/?discussion=BYccvJ
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2.买卖股票的最佳时机 II 贪心算法
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
题源:https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/x2zsx1/
示例 1: 输入: prices = [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2: 输入: prices = [1,2,3,4,5] 输出: 4 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3: 输入: prices = [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
贪心算法的框架
从问题的某一初始解出发:
while (朝给定总目标前进一步)
{
利用可行的决策,求出可行解的一个解元素。
}
由所有解元素组合成问题的一个可行解;
贪心算法参考:https://www.jianshu.com/p/ab89df9759c8
思路:
循环(第一天开始,循环到第n天)//prices=[第1天,…,第n天]
{
//判断是否是买入时机
//这天和后一天相比较:
if 这天<后一天:
买入,记下买入的这天;
//判断是否是卖出时机
if 已经买入:
//是否是最后一天?
if 这天是最后一天:
卖出,卖出的这天-买入的那天
计算卖出的总价格
跳出循环;
if 这天>后一天:
卖出,卖出的这天-买入的那天
计算卖出的总价格
}
python实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
day=0 #第n天
buy=0 #是否买入,1不可买,0可买
buy_day=0 #本次买入时间
money=0#总利润
allday=len(prices)
while day<allday:
if day == allday-1:
if buy==1:
money=money+prices[day]-prices[buy_day]
break
if buy == 1:
if prices[day]>prices[day+1]:
buy=0 #卖掉
money=money+prices[day]-prices[buy_day]#计算收益
if buy==0:
if prices[day]<prices[day+1]:
buy=1#买入
buy_day=day#记下买入时间
day=day+1#新的一天开始啦
return money
3. 缺失的第一个正数 数组排序 困难
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
https://leetcode-cn.com/problems/first-missing-positive/
算法的时间复杂度和空间复杂度
https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/r81qpe/
时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述。
时间复杂度
根据从小到大排列,常见的算法时间复杂度主要有:
O(1)
1、平方 O(N^2) :冒泡排序
2、指数 O(2^N) :递归
算法中,指数阶常出现于递归,算法原理图与代码如下所示。
def algorithm(N):
if N <= 0: return 1
count_1 = algorithm(N - 1)
count_2 = algorithm(N - 1)
return count_1 + count_2
3、对数 O(logN) :
对数阶与指数阶相反,指数阶为 “每轮分裂出两倍的情况” ,而对数阶是 “每轮排除一半的情况” 。对数阶常出现于「二分法」、「分治」等算法中,体现着 “一分为二” 或 “一分为多” 的算法思想。
def algorithm(N):
count = 0
i = N
while i > 1:
i = i / 2
count += 1
return count
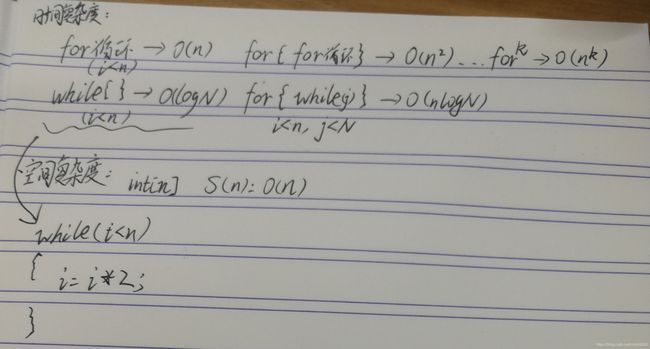
https://zhuanlan.zhihu.com/p/50479555
空间复杂度
空间复杂度涉及的空间类型有:
输入空间: 存储输入数据所需的空间大小;
暂存空间: 算法运行过程中,存储所有中间变量和对象等数据所需的空间大小;
输出空间: 算法运行返回时,存储输出数据所需的空间大小;
通常情况下,空间复杂度指在输入数据大小为 N 时,算法运行所使用的「暂存空间」+「输出空间」的总体大小。


时空权衡
对于算法的性能,需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性,即时间和空间复杂度皆较低。而实际上,对于某个算法问题,同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度,往往是以提升空间复杂度为代价的,反之亦然。
由于当代计算机的内存充足,通常情况下,算法设计中一般会采取「空间换时间」的做法,即牺牲部分计算机存储空间,来提升算法的运行速度。
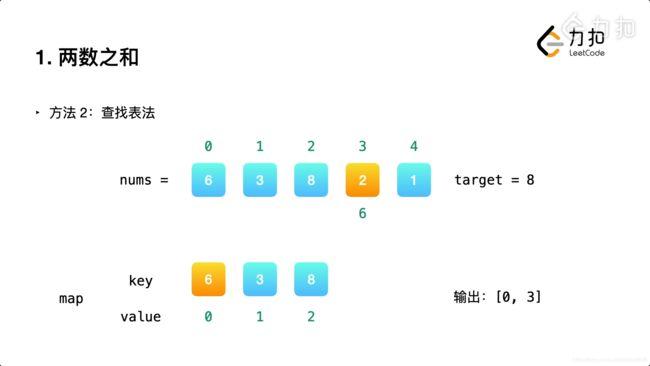
以 LeetCode 全站第一题 两数之和 为例,「暴力枚举」和「辅助哈希表」分别为「空间最优」和「时间最优」的两种算法。
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个
整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
暴力枚举
https://www.cnblogs.com/bigbigli/p/13279909.html
枚举的概念
枚举就是列出一个范围内的所有成员的程序,或者说是将所有情况都举出,并判断其是否符合题目条件,生活中常见的枚举有星期,里面有星期一、星期二… …星期日… …
在C++里面最常见的枚举就是数组的for循环,这种循环就是把数组中的每一个元素都列举一遍。
枚举的优缺点
优点:1.能举出所有情况,保证解为正确解。
2.能解决许多用其他算法难以解决的问题。
3.便于思考与编程。
缺点:为何要叫做暴力枚举呢?因为暴力出奇迹,但是暴力在大多数情况下都是不可取。枚举仅适用于一些规模较小的问题。(否则可能会超时)
时间复杂度 O(N^2) ,空间复杂度 O(1);属于「时间换空间」,虽然仅使用常数大小的额外空间,但运行速度过慢。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int size = nums.size();
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
if (nums[i] + nums[j] == target)
return { i, j };
}
}
return {};
}
};
辅助哈希表
时间复杂度 O(N) ,空间复杂度 O(N) ;属于「空间换时间」,借助辅助哈希表 dic ,通过保存数组元素值与索引的映射来提升算法运行效率,是本题的最佳解法。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int size = nums.size();
unordered_map<int, int> dic;
for (int i = 0; i < size; i++) {
if (dic.find(target - nums[i]) != dic.end()) {
return { dic[target - nums[i]], i };
}
dic.emplace(nums[i], i);
}
return {};
}
};
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> hashtable;
for (int i=0;i<nums.size();++i){
auto it=hashtable.find(target-nums[i]);
if(it!=hashtable.end()){
return {it->second,i};
}
hashtable[nums[i]]=i;
}
return {};
}
};
python用字典来完成哈希表
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashtable={}
for i in range(len(nums)):
tmp=target-nums[i]
if hashtable.get(tmp)==None:
hashtable[nums[i]]=i
else:
return [hashtable[tmp],i]
return []
4、数组矩阵原地旋转
https://leetcode-cn.com/problems/rotate-matrix-lcci/solution/xuan-zhuan-ju-zhen-by-leetcode-solution/
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotate-matrix-lcci
观察找规律

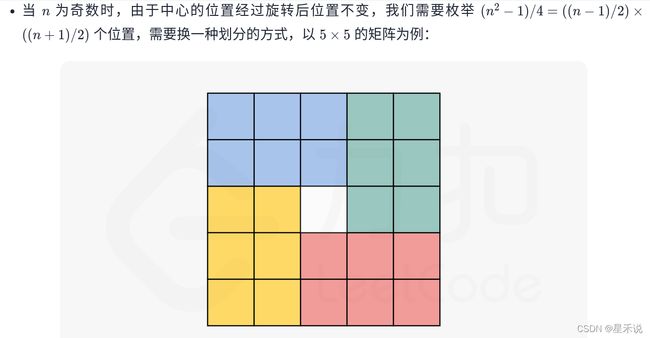
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n=len(matrix)
if n>0:
I=int(n/2)
J=int((n+1)/2)
for r in range(I):
for c in range(J):
tmp=matrix[r][c]
matrix[r][c]=matrix[n-c-1][r]
matrix[n-c-1][r]=matrix[n-r-1][n-c-1]
matrix[n-r-1][n-c-1]=matrix[c][n-r-1]
matrix[c][n-r-1]=tmp
```python
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
for i in range(n // 2):
for j in range((n + 1) // 2):
matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
= matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]
复杂度分析
时间复杂度:O(N^2)O(N
2
),其中 NN 是 \textit{matrix}matrix 的边长。我们需要枚举的子矩阵大小为 O(\lfloor n/2 \rfloor \times \lfloor (n+1)/2 \rfloor) = O(N^2)⌊n/2⌋×⌊(n+1)/2⌋)=O(N
2
)。
空间复杂度:O(1)O(1)。为原地旋转。
python // 整除向小取整
数据结构之哈希表
https://www.cnblogs.com/s-b-b/p/6208565.html
一个好的哈希函数需要有以下特点:
1.尽量使关键字对应的记录均匀分配在哈希表里面(比如说某厂商卖30栋房子,均匀划分ABC3个区域,如果你划分A区域1个房子,B区域1个房子,C区域28个房子,有人来查找C区域的某个房子最坏的情况就是要找28次)。
2.关键字极小的变化可以引起哈希值极大的变化。比较好的哈希函数是time33算法。PHP的数组就是把这个作为哈希函数。
unsigned long hash(const char* key){
unsigned long hash=0;
for(int i=0;i<strlen(key);i++){
hash = hash*33+str[i];
}
return hash;
}
由于哈希表高效的特性,查找或者插入的情况在大多数情况下可以达到O(1)
解题
1.哈希表解题
如果本题没有额外的时空复杂度要求,那么就很容易实现:
- 我们可以将数组所有的数放入哈希表,随后从 1 开始依次枚举正整数,并判断其是否在哈希表中;
- 我们可以从 1 开始依次枚举正整数,并遍历数组,判断其是否在数组中。
如果数组的长度为 N,那么第一种做法的时间复杂度为 O(N),空间复杂度为 O(N);第二种做法的时间复杂度为 O(N^2),空间复杂度为 O(1)。但它们都不满足时间复杂度为 O(N) 且空间复杂度为 O(1)。
思路
实际上,对于一个长度为 N 的数组,其中没有出现的最小正整数只能在 [1, N+1] 中。这是因为如果 [1, N]都出现了,那么答案是 N+1,否则答案是 [1, N]中没有出现的最小正整数。这样一来,我们将所有在 [1,N] 范围内的数放入哈希表,也可以得到最终的答案。
方法:
我们对数组进行遍历,对于遍历到的数 x,如果它在 [1, N]的范围内,那么就将数组中的第 x-1 个位置(注意:数组下标从 00 开始)打上「标记」。在遍历结束之后,如果所有的位置都被打上了标记,那么答案是 N+1,否则答案是最小的没有打上标记的位置加 11。


C++实现:
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
int n = nums.size();//确定数组大小n
for (int& num: nums) {
if (num <= 0) {
num = n + 1;
}
}//遍历数组,把负数标为n+1
for (int i = 0; i < n; ++i) {//
int num = abs(nums[i]);//找到对应数组元素的绝对值参数
if (num <= n) {
nums[num - 1] = -abs(nums[num - 1]);//在1到n范围内,标记成负数
}
}
for (int i = 0; i < n; ++i) {
if (nums[i] > 0) {
return i + 1; //遍历到第一个正整数,返回i+1即可
}
}
return n + 1;//全部遍历完,则最小正整数为n+1
}
};
4、给定一个整数数组,判断是否存在重复元素。简单
如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
思路:
1、排序
2、比较相邻元素是否相等
1、排序:
https://blog.csdn.net/liang_gu/article/details/80627548
1.1 冒泡排序
首先从数组的第一个元素开始到数组最后一个元素为止,对数组中相邻的两个元素进行比较,如果位于数组左端的元素大于数组右端的元素,则交换这两个元素在数组中的位置,此时数组最右端的元素即为该数组中所有元素的最大值。接着对该数组剩下的n-1个元素进行冒泡排序,直到整个数组有序排列。算法的时间复杂度为O(n^2)。
// 冒泡排序
void BubbleSort(int arr[], int length)
{
for (int i = 0; i < length; i++)
{
for (int j = 0; j < length - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
int temp;
temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
题解一:类似冒泡排序,超出时间复杂度,用了两个for循环,时间复杂度为O(n^2)
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
int length=nums.size();
for( int i=0; i<length; i++)
{
for( int j=0; j<length-1-i; j++)
{
int temp=i+j+1;
if(nums[i]==nums[temp])
{
return true;
break;
}
}
}
return false;
}
};
1.2 归并排序
“归并”的含义是将两个或两个以上的有序序列组合成一个新的有序表。假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到(表示不小于x的最小整数)个长度为2(或者是1)的有序子序列,再两两归并。如此重复,直到得到一个长度为n的有序序列为止。这种排序方法称为2-路归并排序。

// 归并排序
void MergeSort(int arr[], int start, int end, int * temp)
{
if (start >= end)
return;
int mid = (start + end) / 2;
MergeSort(arr, start, mid, temp);
MergeSort(arr, mid + 1, end, temp);
// 合并两个有序序列
int length = 0; // 表示辅助空间有多少个元素
int i_start = start;
int i_end = mid;
int j_start = mid + 1;
int j_end = end;
while (i_start <= i_end && j_start <= j_end)
{
if (arr[i_start] < arr[j_start])
{
temp[length] = arr[i_start];
length++;
i_start++;
}
else
{
temp[length] = arr[j_start];
length++;
j_start++;
}
}
while (i_start <= i_end)
{
temp[length] = arr[i_start];
i_start++;
length++;
}
while (j_start <= j_end)
{
temp[length] = arr[j_start];
length++;
j_start++;
}
// 把辅助空间的数据放到原空间
for (int i = 0; i < length; i++)
{
arr[start + i] = temp[i];
}
}
关于代码的理解可以参考以下博客:
https://www.cnblogs.com/chengxiao/p/6194356.html



题解二:归并排序+找相邻元素 通过
class Solution {
public:
void MergeSort(int arr[], int start, int end, int temp[]){
if(start >= end)
return;
int mid=(start+end)/2;
MergeSort(arr,start,mid,temp);
MergeSort(arr,mid+1,end,temp);
int i_start=start;
int i_end=mid;
int j_start=mid+1;
int j_end=end;
int length=0;
while(i_start<=i_end && j_start<=j_end){
if(arr[i_start]<=arr[j_start]){
temp[length]=arr[i_start];
length++;
i_start++;
}
if(arr[j_start]<arr[i_start]){
temp[length]=arr[j_start];
length++;
j_start++;
}
}
while (i_start <= i_end)
{
temp[length] = arr[i_start];
i_start++;
length++;
}
while (j_start <= j_end)
{
temp[length] = arr[j_start];
length++;
j_start++;
}
// 把辅助空间的数据放到原空间
for (int i = 0; i < length; i++)
{
arr[start + i] = temp[i];
}
}
bool containsDuplicate(vector<int>& nums) {
int len=nums.size();
int temp[len];
int s=0;
int e=len-1;
int arr[len];
for(int j=0;j<len;j++){
arr[j]=nums[j];
}
MergeSort(arr,s,e,temp);
for(int i=0;i<len-1;i++){
if(arr[i]==arr[i+1])
return true;
}
return false;
}
};
链表
单向链表
双向链表
//双向链表节点结构
typedef struct dlink_node
{
struct dlink_node *prev;
struct dlink_node *next;
void *val; //能存储任意类型数据
}node;
题目
初级算法
1、删除链表的倒数第N个节点,求解链表长度
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
private: int length(ListNode* head){//求解链表长度
int len=0;
while(head!=nullptr){
len++;
head=head->next;
}
return len;
}
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
int line=length(head);
ListNode* del=head;
int last=line-n;
if(last==0){//如果倒数n个节点是头节点
return head=head->next;
}
for(int i=0;i<last-1;i++){
del=del->next;//找到倒数第n个节点前一个节点
}
del->next=del->next->next;//删除第n个节点
return head;//返回头节点
}
};
执行结果:
通过
显示详情
执行用时:8 ms, 在所有 C++ 提交中击败了33.02% 的用户
内存消耗:10.4 MB, 在所有 C++ 提交中击败了74.30% 的用户
2、链表的反转
2.1 双链表双指针求解
新设置一个链表,不断更新该链表的头节点
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* newhead=nullptr;//定义一个新链表
while(head!=nullptr){
ListNode* temp=head->next;//缓存原链表下一个节点
head->next=newhead;//链表下一节点连接新链表
newhead=head;//保存新链表
head=temp;//head指向原链表下一个节点
}
return newhead;//循环结束,返回新链表,即为反转后的链表
}
};
执行结果:
通过
显示详情
执行用时:4 ms, 在所有 C++ 提交中击败了92.65% 的用户
内存消耗:8.1 MB, 在所有 C++ 提交中击败了49.20% 的用户
2.2 栈求解
java
public ListNode reverseList(ListNode head) {
Stack<ListNode> stack = new Stack<>();
//把链表节点全部摘掉放到栈中
while (head != null) {
stack.push(head);
head = head.next;
}
if (stack.isEmpty())
return null;
ListNode node = stack.pop();
ListNode dummy = node;
//栈中的结点全部出栈,然后重新连成一个新的链表
while (!stack.isEmpty()) {
ListNode tempNode = stack.pop();
node.next = tempNode;
node = node.next;
}
//最后一个结点就是反转前的头结点,一定要让他的next
//等于空,否则会构成环
node.next = null;
return dummy;
}
作者:sdwwld
链接:https://leetcode-cn.com/problems/reverse-linked-list/solution/shu-ju-jie-gou-he-suan-fa-zhan-shuang-li-xv2d/
来源:力扣(LeetCode)
3、合并两个有序链表
采用迭代的方法
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* preHead= new ListNode(-1);
ListNode* prev = preHead;//设置指针指向新的链表
while(l1!=nullptr&&l2!=nullptr){
if(l1->val <l2->val){
prev->next=l1;
l1=l1->next;//l1指针向后移动一位
}
else{
prev->next=l2;
l2=l2->next;//l2指针向后移动一位
}
prev=prev->next;
}
if(l1!=nullptr){
prev->next=l1;
}
if(l2!=nullptr){
prev->next=l2;
}
return preHead->next;
}
};
执行结果:
执行用时:8 ms, 在所有 C++ 提交中击败了73.24% 的用户
内存消耗:14.4 MB, 在所有 C++ 提交中击败了65.92% 的用户
4、判断回文链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
private:
int length(ListNode* head){//求解链表长度
int len=0;
while(head!=nullptr){
len++;
head=head->next;
}
return len;
}
void CopyList(ListNode* L,ListNode* M, int n)
{ // 给链表插入n个数据
ListNode* p=L;
ListNode* q=M;
for (int i = 0; i < n; i++)
{
ListNode* h = new ListNode(-1); // 生成头结点
h->val=p->val;
h->next=nullptr;
q->next=h;
q=q->next;
p=p->next;
}
q->next=nullptr;
}
public:
bool isPalindrome(ListNode* head) {
ListNode* newhead=nullptr;
ListNode* oldhead=new ListNode(-1);
int n=length(head);
CopyList(head,oldhead,n);
oldhead=oldhead->next;
while(head!=nullptr){
ListNode* temp=head->next;//暂存链表下一节点
head->next=newhead;//链表下一节点连接新链表
newhead=head;//保存更新的新链表
head=temp;//原链表指向下一节点
}
while(newhead!=nullptr&&oldhead!=nullptr&&newhead->val==oldhead->val){
newhead=newhead->next;
oldhead=oldhead->next;
}
if(newhead==nullptr&&oldhead==nullptr){
return true;
}
else
return false;
}
};
思路:反转链表,判断反转后的链表和之前的链表是否相同
难点:怎么复制保存之前的链表,两个链表之间怎样比较是否相同
在visual studio code中的调试程序
#include执行用时:216 ms, 在所有 C++ 提交中击败了62.30% 的用户
内存消耗:137.5 MB, 在所有 C++ 提交中击败了4.99% 的用户
进阶 你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
https://leetcode-cn.com/leetbook/read/top-interview-questions-easy/xnv1oc/
5、环形链表
 输入:head = [3,2,0,-4], pos = 1
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
快慢指针解决
队列
queue<int> que;
que.push(1); // 元素 1 入队
que.push(2); // 元素 2 入队
que.pop(); // 出队 -> 元素 1
que.pop(); // 出队 -> 元素 2
栈
stack<int> stk;
stk.push(1); // 元素 1 入栈
stk.push(2); // 元素 2 入栈
stk.top();//返回栈顶元素2,栈内元素不变
stk.pop(); // 出栈 -> 元素 2返回空void
stk.pop(); // 出栈 -> 元素 1
stk.empty();//判断是否为空值
动态数组实现栈C++
(一般情况用上面的栈函数就可以了不必自己写了解即可)
#include 1、每日温度
请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
作者:力扣 (LeetCode)
链接:https://leetcode-cn.com/leetbook/read/queue-stack/genw3/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n=temperatures.size();
stack<int> stk;
vector<int> output(n);
for(int i=0;i<n;i++){
while(!stk.empty()&&temperatures[i]>temperatures[stk.top()]){
int idx=stk.top();
output[idx]=i-idx;
stk.pop();
}
stk.push(i);
}
return output;
}
};
执行结果:
通过
显示详情
执行用时:152 ms, 在所有 C++ 提交中击败了50.38% 的用户
内存消耗:86.8 MB, 在所有 C++ 提交中击败了43.79% 的用户
栈和DFS深度优先搜索
https://leetcode-cn.com/leetbook/read/queue-stack/gro21/
例子一从A节点找到G节点的路径

在上面的例子中,我们从根结点 A 开始。首先,我们选择结点 B 的路径,并进行回溯,直到我们到达结点 E,我们无法更进一步深入。然后我们回溯到 A 并选择第二条路径到结点 C 。从 C 开始,我们尝试第一条路径到 E 但是 E 已被访问过。所以我们回到 C 并尝试从另一条路径到 F。最后,我们找到了 G。
总的来说,在我们到达最深的结点之后,我们只会回溯并尝试另一条路径。
因此,你在 DFS 中找到的第一条路径并不总是最短的路径。例如,在上面的例子中,我们成功找出了路径 A-> C-> F-> G 并停止了 DFS。但这不是从 A 到 G 的最短路径。
栈操作:
如上面的动画所示,我们首先将根结点推入到栈中;然后我们尝试第一个邻居 B 并将结点 B 推入到栈中;等等等等。当我们到达最深的结点 E 时,我们需要回溯。当我们回溯时,我们将从栈中弹出最深的结点,这实际上是推入到栈中的最后一个结点。
树
一些概念总结
节点的度:一个节点含有的子树的个数称为该节点的度;
树的度:一棵树中,最大的节点度称为树的度;
叶节点或终端节点:度为零的节点;
非终端节点或分支节点:度不为零的节点;
父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
堂兄弟节点:父节点在同一层的节点互为堂兄弟;
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m(m>=0)棵互不相交的树的集合称为森林;
作者:sdwwld
链接:https://leetcode-cn.com/problems/balanced-binary-tree/solution/shu-ju-jie-gou-he-suan-fa-ping-heng-er-c-ckkm/
1、简单题:求二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/
15 7
题解一 深度优先搜索(DFS)
如果我们知道了左子树和右子树的最大深度 l 和 r,那么该二叉树的最大深度即为
max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在 O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
复杂度分析
时间复杂度:O(n)O(n)O(n),其中 nnn 为二叉树节点的个数。每个节点在递归中只被遍历一次。
空间复杂度:O(height)O(\textit{height})O(height),其中 height\textit{height}height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
题解二 广度优先搜索(BFS)
BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。一般用队列数据结构来辅助实现BFS算法。
我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量 ans 来维护拓展的次数,该二叉树的最大深度即为ans。
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
queue<TreeNode*> Q;
Q.push(root);
int ans = 0;
while (!Q.empty()) {
int sz = Q.size();
while (sz > 0) {
TreeNode* node = Q.front();Q.pop();
if (node->left) Q.push(node->left);
if (node->right) Q.push(node->right);
sz -= 1;
}
ans += 1;
}
return ans;
}
};
2、平衡二叉搜索数AVL(实现代码未看)
https://blog.csdn.net/tanrui519521/article/details/80935348
平衡二叉搜索树,它能保持二叉树的高度平衡,尽量降低二叉树的高度,减少树的平均查找长度。
AVL树的性质:
左子树与右子树高度之差的绝对值不超过1
树的每个左子树和右子树都是AVL树
每一个节点都有一个平衡因子(balance factor),任一节点的平衡因子是-1、0、1(每一个节点的平衡因子 = 右子树高度 - 左子树高度)
题目剑指判断平衡二叉树
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
自顶向下
int height(TreeNode* root) {
if (root == NULL) {
return 0;
} else {
return max(height(root->left), height(root->right)) + 1;
}
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
} else {
return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
}
自底向上
class Solution {
public:
int height(TreeNode* root) {
if (root == NULL) {
return 0;
}
int leftHeight = height(root->left);
int rightHeight = height(root->right);
if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return max(leftHeight, rightHeight) + 1;
}
}
bool isBalanced(TreeNode* root) {
return height(root) >= 0;
}
};
堆
根据 维基百科 的定义,堆 是一种特别的二叉树,满足以下条件的二叉树,可以称之为 堆:
完全二叉树;
每一个节点的值都必须 大于等于或者小于等于 其孩子节点的值。
堆 具有以下的特点:
可以在 O(logN)O(logN) 的时间复杂度内向 堆 中插入元素;
可以在 O(logN)O(logN) 的时间复杂度内向 堆 中删除元素;
可以在 O(1)O(1) 的时间复杂度内获取 堆 中的最大值或最小值。
堆 有两种类型:最大堆 和 最小堆。
最大堆:堆中每一个节点的值 都大于等于 其孩子节点的值。所以最大堆的特性是 堆顶元素(根节点)是堆中的最大值。
最小堆:堆中每一个节点的值 都小于等于 其孩子节点的值。所以最小堆的特性是 堆顶元素(根节点)是堆中的最小值。

堆 在大部分编程语言中,都已经有内置方法实现它。所以,一般来说并不需要我们去实现一个 堆 。而对于使用者来说,我们需要掌握堆在对应的编程语言中的常用方法,使我们能灵活的运用 堆 。
本章节将带你学会:
如何创建 最大堆 和 最小堆;
如何往 堆 中插入元素;
如何获取堆顶元素;
如何删除堆顶元素;
如何获取 堆 的长度;
堆 常用方法的时间复杂度和空间复杂度分析。
创建堆
import heapq
# 创建一个空的最小堆
minHeap = []
heapq.heapify(minHeap)
# 创建一个空的最大堆
# 由于Python中并没有内置的函数可以直接创建最大堆,所以一般我们不会直接创建一个空的最大堆。
# 创建带初始值的「堆」, 或者称为「堆化」操作,此时的「堆」为「最小堆」
heapWithValues = [3,1,2]
heapq.heapify(heapWithValues)
# 创建最大堆技巧
# Python中并没有内置的函数可以直接创建最大堆。
# 但我们可以将[每个元素*-1],再将新元素集进行「堆化」操作。此时,堆顶元素是新的元素集的最小值,也可以转换成原始元素集的最大值。
# 示例
maxHeap = [1,2,3]
maxHeap = [-x for x in maxHeap]
heapq.heapify(maxHeap)
# 此时的maxHeap的堆顶元素是-3
# 将-3转换为原来的元素3,既可获得原来的maxHeap中最大的值是3
插入元素
最小堆插入元素最大堆插入元素
元素乘以-1的原因是我们将最小堆转换为最大堆。
# 最小堆插入元素
heapq.heappush(minHeap, 1)
# 最大堆插入元素
# 元素乘以-1的原因是我们将最小堆转换为最大堆。
heapq.heappush(maxHeap, 1*-1)
时间复杂度: O(log N)
空间复杂度: O(1)
# 最小堆获取堆顶元素,即最小值
minHeap[0]
# 最大堆获取堆顶元素,即最大值
# 元素乘以 -1 的原因是:我们之前插入元素时,将元素乘以 -1,所以在获取元素时,我们需要乘以 -1还原元素。
maxHeap[0]*-1
删除堆顶元素
# 最小堆删除堆顶元素
heapq.heappop(minHeap)
# 最大堆删除堆顶元素
heapq.heappop(maxHeap)
获取堆的长度
# 最小堆的长度
len(minHeap)
# 最大堆的长度
len(maxHeap)
应用——堆排序
理论:堆排序指的是利用堆的数据结构对一组无序元素进行排序。
最小堆 排序算法步骤如下:
将所有元素堆化成一个 最小堆 ;
取出并删除堆顶元素,并将该堆顶元素放置在存储有序元素的数据集 T 中;
此时,堆 会调整成新的 最小堆;
重复 3 和 4 步骤,直到 堆 中没有元素;
此时得到一个新的数据集 T,其中的元素按照 从小到大 的顺序排列。
最大堆排序算法步骤如下:
将所有元素堆化成一个 最大堆;
取出并删除堆顶元素,并将该堆顶元素放置在存储有序元素的数据集 T 中;
此时,堆 会调整成新的 最大堆;
重复3和4步骤,直到堆中没有元素;
此时得到一个新的数据集T,其中的元素按照从大到小的顺序排列。
时间复杂度:O(NlogN)。N是堆中的元素个数。
空间复杂度:O(N)。N是 堆 中的元素个数。
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
我们用一个大根堆实时维护数组的前 k 小值。首先将前 k 个数插入大根堆中,随后从第 k+1个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。在下面的代码中,由于 C++ 语言中的堆(即优先队列)为大根堆,我们可以这么做。而 Python 语言中的堆为小根堆,因此我们要对数组中所有的数取其相反数,才能使用小根堆维护前 k 小值。
输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1]
输入:arr = [0,1,2,1], k = 1输出:[0]
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> vec(k, 0);创建一个元素k,元素值为0
if (k == 0) { // 排除 0 的情况
return vec;
}
priority_queue<int> Q;
for (int i = 0; i < k; ++i) {
Q.push(arr[i]);//k个数放进来,排列从大到小
}
for (int i = k; i < (int)arr.size(); ++i) {//后面的k个数与堆顶元素做比较
if (Q.top() > arr[i]) {//如果堆顶元素比后面的元素大,换掉它
Q.pop();
Q.push(arr[i]);
}
}
for (int i = 0; i < k; ++i) {//把堆中元素推出到vec容器里
vec[i] = Q.top();
Q.pop();
}
return vec;
}
};
图
并查集( Union Find )数据结构
「图」的深度优先搜索算法
「图」的广度优先搜索算法
最小生成树相关定理和算法
切分定理
Kruskal 算法
Prim 算法
单源最短路径相关算法
Dijkstra 算法
Bellman-Ford 算法
拓扑排序之 Kahn 算法
一、并查集
quick find伪代码:
quick union
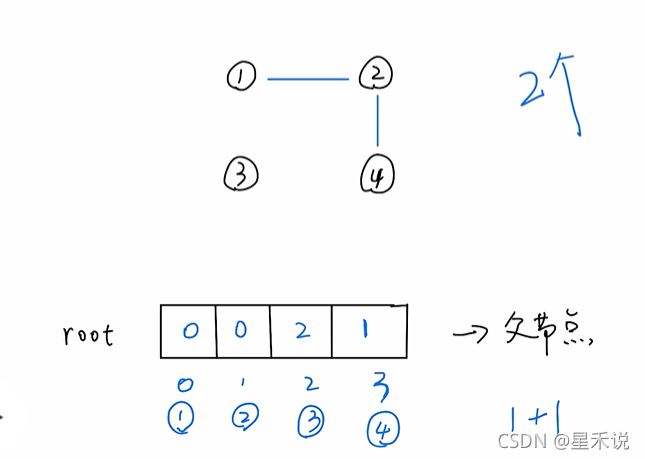
题目——力扣 547 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
class UnionFind{
public:
vector<int> root;
vector<int> rank;
UnionFind(int size):root(size),rank(size){
for(int i=0;i<size;i++){
root[i]=i;
rank[i]=1;
}
}
int find(int x){
if(x == root[x])
return x;
return root[x]=find(root[x]);
}
void union1(int x,int y){
int rootX=find(x);
int rootY=find(y);
if(rootX!=rootY){
if(rank[rootX]>rank[rootY]){
root[rootY]=rootX;
}
if(rank[rootX]<rank[rootY]){
root[rootX]=rootY;
}
if(rank[rootX]==rank[rootY]){
root[rootY]=rootX;
rank[rootX]+=1;
}
}
}
bool connected(int x,int y){
return find(x)==find(y);
}
int rootnumber(){
int flag=0;
for(int i=0;i<root.size();i++){
if(i==root[i])
flag++;
}
return flag;
}
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int n=isConnected.size();
UnionFind uf(n);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(isConnected[i][j]==1 && i!=j)
{
uf.union1(i,j);
}
}
}
return uf.rootnumber();
}
};
执行结果:
通过
显示详情
执行用时:
20 ms
, 在所有 C++ 提交中击败了
77.93%
的用户
内存消耗:
13.4 MB
, 在所有 C++ 提交中击败了
49.48%
的用户
通过测试用例:
113 / 113
总结
作者:爱学习的饲养员
链接:https://leetcode-cn.com/leetbook/read/graph/r3f173/
来源:力扣(LeetCode)
「并查集」数据结构总结
在「并查集」数据结构中,其中心思想是将所有连接的顶点,无论是直接连接还是间接连接,都将他们指向同一个父节点或者根节点。此时,如果要判断两个顶点是否具有连通性,只要判断它们的根节点是否为同一个节点即可。
在「并查集」数据结构中,它的两个灵魂函数,分别是 find和 union。find 函数是为了找出给定顶点的根节点。 union 函数是通过更改顶点根节点的方式,将两个原本不相连接的顶点表示为两个连接的顶点。对于「并查集」来说,它还有一个重要的功能性函数 connected。它最主要的作用就是检查两个顶点的「连通性」。find 和 union 函数是「并查集」中必不可少的函数。connected 函数则需要根据题目的意思来决定是否需要。
「并查集」代码基本结构
Java
public class UnionFind {
// UnionFind 的构造函数,size 为 root 数组的长度
public UnionFind(int size) {}
public int find(int x) {}
public void union(int x, int y) {}
public boolean connected(int x, int y) {}
}
「并查集」的 find 函数
它主要是用于查找顶点 x 的根结点。
find 函数的基本实现
public int find(int x) {
while (x != root[x]) {
x = root[x];
}
return x;
}
find 函数的优化 - 路径压缩
public int find(int x) {
if (x == root[x]) {
return x;
}
return root[x] = find(root[x]);
}
「并查集」的 union 函数
它主要是连接两个顶点 x 和 y 。将它们的根结点变成相同的,即代表它们来自于同一个根节点。
union 函数的基本实现
Java
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
root[rootY] = x;
}
};
union 函数的优化 - 按秩合并
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
};
「并查集」的 connected 函数
它主要是检查两个顶点 x 和 y 的「连通性」。这个函数通过顶点 x 和 y 的根结点是否相同来判断 x 和 y 的「连通性」。如果 x 和 y 的根结点相同,则为连通。反之,则为不连通。
Java
public boolean connected(int x, int y) {
return find(x) == find(y);
}
「并查集」的刷题小技巧
「并查集」的代码是高度模版化的。所以作者建议大家熟记「并查集」的实现代码,这样小伙伴们在遇到「并查集」的算法题目的时候,就可以淡定的应对了。作者推荐大家在理解的前题下,请熟记**「基于路径压缩+按秩合并的并查集」的实现代码。**
最后,请小伙伴们尝试用「并查集」以及刚刚熟记的代码,实现后面「并查集」相关的练习题。虽然,一道算法题可以有很多种解法,但是作者还是非常建议大家用「并查集」的思想实现该章节的算法练习题哦。
按秩合并的并查集

对于合并最左边的两棵树,最后面一种以0为根节点的方法效率更高。

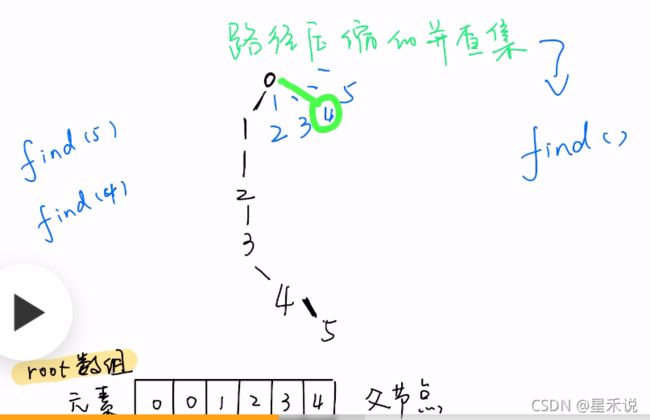
基于路径压缩的并查集
将秩合并和路径压缩结合♥♥
// UnionFind.class
public class UnionFind {
int root[];
// 添加了 rank 数组来记录每个顶点的高度,也就是每个顶点的「秩」
int rank[];
public UnionFind(int size) {
root = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
rank[i] = 1; // 一开始每个顶点的初始「秩」为1,因为它们只有自己本身的一个顶点。
}
}
// 此处的 find 函数与路径压优化缩版本的 find 函数一样。
public int find(int x) {
if (x == root[x]) {
return x;
}
return root[x] = find(root[x]);
}
// 按秩合并优化的 union 函数
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
};
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// 测试样例
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}
作者:爱学习的饲养员
链接:https://leetcode-cn.com/leetbook/read/graph/r3jbih/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
二、图的深度优先搜索
题目 797. 所有可能的路径
https://leetcode-cn.com/problems/all-paths-from-source-to-target/
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点,空就是没有下一个结点了。
译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a 。

即索引0对应1,2
索引1对应3,索引2对应3,索引3不对应任何
图的深度为3,从0开始找,所以先把0放入栈中,从索引0开始找,找到1,把1压入栈内,递归从索引1开始找,找到3,3压入栈中,3是最大深度,路径就是栈中的路径。
把3出栈,回去找1没有其它路径,for(auto& y:graph[x])即找索引x层的单元数组元素,把1出栈,回去找0的下一个路径,也就是2,索引2在继续找。
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
class Solution {
public:
vector<vector<int>> ans;
vector<int> stk;
void dfs(vector<vector<int>>& graph, int x, int n) {
if (x == n) {
ans.push_back(stk);
return;
}
for (auto& y : graph[x]) {
stk.push_back(y);
dfs(graph, y, n);
stk.pop_back();
}
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
stk.push_back(0);
dfs(graph, 0, graph.size() - 1);
return ans;
}
};
//测试用例
int main() {
Solution s;
vector<int> B,C,D,E,F;
B.push_back(4);
B.push_back(3);
B.push_back(1);
vector<vector<int>> g;
g.push_back(B);
C.push_back(3);
C.push_back(2);
C.push_back(4);
g.push_back(C);
D.push_back(3);
g.push_back(D);
g.push_back(vector<int> ());
auto a=s.allPathsSourceTarget(g);
}
三、广度优先搜索
「广度优先搜索」算法不仅可以遍历「图」的所有顶点,也可以遍历两个顶点的所有路径。但是,「广度优先搜索」最高效的用途是:当在 权重相等且均为正数的「图」 中,它可以快速的找到两点之间的最短路径。
虽然「深度优先搜索」算法也可以针对权重相等均且为正数的「图」找出两点之间的最短路径,但它需要先找出两点之间的所有路径之后,才可以求出最短路径。但是对于「广度优先搜索」,在大多数情况下,它可以不用找出所有路径,就能取出两点之间的最短路径。除非,最短路径出现在最后一条遍历的路径上,这种情况下,「广度优先搜索」也是遍历出了所有路径后,才取出的最短路径。
编程思路:
定义一个 queue
首先que.push({0})用来放入起始路径
{进入循环,循环条件为que.size()!=0即当它=0时表示我的路径已经全部处理完了
从队列里弹出当前路径curPath=que.front()
并且把这条要处理的路径清除出待处理队列que.pop()
找到curPath队列的末尾节点,node=curPath.back()
{for(int nextNode:graph[node])循环末位节点在图中对应的下一节点
把找到的下一节点放入curPath里
如果发现是末尾节点即重点,则把这条路径放入ret已找到路径中,
否则的话把当前路径放回待处理队列里
最后在curPath中弹出这个已经处理好的路径,进入循环从que中取出下一条待处理的路径
}
}
循环结束,返回ret即可。
class Solution
{
public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph)
{
vector<vector<int>> ret;
if (graph.size() == 0) return ret;
queue<vector<int>> que; // 保存每条路径
// 加入首节点
que.push({0});
while (que.size())
{
// 从队列中弹出当前路径
vector<int> curPath = que.front();
que.pop();
// 末尾节点
int node = curPath.back();
// 下层节点等于目标值入结果集,不再入队
for (int nextNode : graph[node])
{
curPath.push_back(nextNode);
if (nextNode == graph.size() - 1) // 是 nextNode 不是 node 也不是当前 curPath 的 size
ret.push_back(curPath);
else
que.push(curPath);
// 选中下一层一个节点后,遍历下一个下层节点,需要先恢复现场
curPath.pop_back();
}
}
return ret;
}
};
作者:匿名用户
链接:https://leetcode-cn.com/leetbook/read/graph/rq24fj/?discussion=nNaK68
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
算法设计
动态规划
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
设爬n个台阶,有f(n)种方法
n=1,f(1)=1;n=2,f(2)=2;n=3,f(3)=f(1)+f(2)
推f(n)=f(n-1)+f(n-2)
当n过大时,用递归调用不合适,可以用动态规划代替递归调用
class Solution {
public:
int climbStairs(int n) {
if(n<=2)
return n;
int first=1;
int second=2;
int sum=0;
while(n-->2){
sum=first+second;
first=second;
second=sum;
}
return sum;
}
};
执行结果:
通过
显示详情
执行用时:0 ms, 在所有 C++ 提交中击败了100.00% 的用户
内存消耗:5.9 MB, 在所有 C++ 提交中击败了65.71% 的用户