XGBoost理论推导+论文解读-下篇

确定树结构

通常采用贪心法，每次尝试分裂一个叶节点，计算分裂后的增益，选增益最大的。这个方法在之前的决策树算法中大量被使用。而增益的计算方式比如ID3的信息增益，C4.5的信息增益率，CART的Gini系数等。

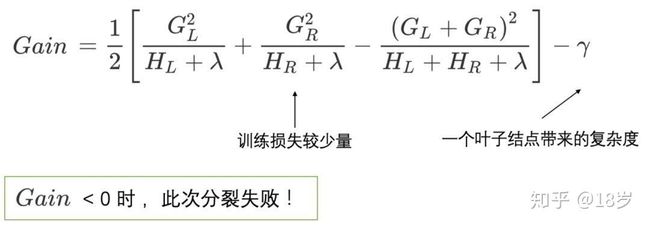
而在XGBoost中，计算增益的公式：
$$\text{ Gain }=\frac{1}{2}[\underset{\text{左子树分数 }}{\frac{G_L^2}{H_L+\lambda }}+\underset{\text{右子树分数 }}{\frac{G_R^2}{H_R+\lambda }}-\underset{\text{分裂前分数 }}{\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }}]-\underset{\text{新叶节点复杂度 }}{\gamma }$$

证明：

$优化目标：minOb{j}^{(t)}-\frac{1}{2}{\sum }_{j=1}^T\left(\frac{G_j^2}{H_j+\lambda }\right)+\gamma$

我们希望损失函数越小越好，也就希望以下式子越大越好：$\frac{({\sum }_{i\in j}{g}_i{)}^2}{{\sum }_{i\in j}{h}_i+\lambda }$，而它正是XGBoost用于分枝时的指标“结构分数”（Structure Score）。

要让目标函数下降，则需要分裂节点来增加模型的复杂度，从而更好地拟合数据

接下来对单个叶子节点进行分析：只对一个节点进行分裂

分裂前：$Ob{j}_{前}=-\frac{1}{2}{\sum }_{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$

分裂后：$Ob{j}_{后}=-\frac{1}{2}{\sum }_{j=1}^{T-1}\frac{G_j^2}{H_j+\lambda }+\gamma (T-1)-\frac{1}{2}\frac{G_L^2}{H_L+\lambda }-\frac{1}{2}\frac{G_R^2}{H_R+\lambda }+2\gamma$

注释：

等号右边前两项是分裂前除了需要分析的父节点以外的其他T-1个节点的损失值，$2\gamma 是由于由一个父节点分裂成左右两个节点（二叉树）$ ，而目标是让obj最小化，也就是 $ob{j}_{后}-ob{j}_{前}\le 0$

$$\begin{gathered} ob{j}_{后}-ob{j}_{前}=\frac{1}{2}\left[\frac{G_L^2}{H_{L_L}+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{G^2}{H+\lambda }\right]-\gamma \\ =\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }\right]-\gamma \end{gathered}$$

此时一开始的优化目标也就变为max $(ob{j}_{后}-ob{j}_{前})$ ，即

$max\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }\right]-2\gamma$

由于每一个结点每一次分裂都会多产生一个节点（二叉树），从而会导致损失函数多一个$\gamma$,每一个节点都会存在这个现象，所以$\gamma$可以忽略不计。

解释父节点的结构分数是$\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }$?

首先每个节点的结构计算公式$$Scor{e}_j=\frac{({\sum }_{i\in j}{g}_i{)}^2}{{\sum }_{i\in j}{h}_i+\lambda }$$，而父节点上的样本相当于左子节点的样本加上右子节点上的样本，再遵循最终的求导结果可以转化为各个样本的求导结果之和，所以最终的结果是$\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }$。

结构分数的意义

$$\begin{gathered} Scor{e}_j=\frac{节点j上所有样本的一阶导数之和的平方}{节点j上所有样本的二阶导数之和+\lambda } \\ =\frac{({\sum }_{i\in L}{g}_i{)}^2}{{\sum }_{i\in L}{h}_i+\lambda }+\frac{({\sum }_{i\in R}{g}_i{)}^2}{{\sum }_{i\in R}{h}_i+\lambda }-\frac{({\sum }_{i\in P}{g}_i{)}^2}{{\sum }_{i\in P}{h}_i+\lambda } \end{gathered}$$

与信息熵、基尼系数等可以评价单一节点的指标不同，结构分数只能够评估结构本身的优劣，不能评估节点的优劣，分数越高则说明树结构质量越高。

例子：

样本	y	y_hat
1	1	0.5
2	-2	0.5
3	-2	0.5

• 分割方案1:（1,23）

左子节点	y	y_hat		右子节点	y	y_hat
1	1	0.5		2	-2	0.5
				3	-2	0.5

• 分割方案2:（12,3）

左子节点	y	y_hat		右子节点	y	y_hat
1	1	0.5		3	-2	0.5
2	-2	0.5

假设现在执行的是XGBoost回归，损失函数为0.5倍MSE，公式为$\frac{1}{2}(y-\hat{y}{)}^2$，假设lambda=1。那基于MSE的一阶导数为：

$$\begin{array}{rl}l& =\frac{1}{2}(y_i-\widehat{y_i}{)}^2\\ & \\ l^{\prime }& =\frac{\partial }{\partial \widehat{y_i}}\frac{1}{2}(y_i-\widehat{y_i}{)}^2\\ & \\ & =-(y_i-\widehat{y_i})\\ & \\ & =\widehat{y_i}-y_i\\ & \end{array}$$

基于MSE的二阶导数为：

$$\begin{array}{rl}{l}^{\prime \prime }& =\frac{\partial }{\partial \widehat{y_i}}(\widehat{y_i}-y_i)\\ & \\ & =1\end{array}$$

方案	左侧结构分数	右侧结构分数	父节点结构分数	增益
(1,23)	0.125	8.333	5.0625	3.3958
(12,3)	1.333	3.125	5.0625	-0.6041

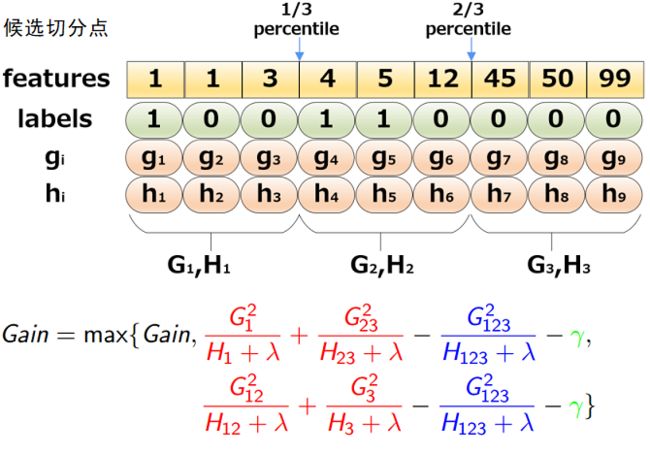
因此，每次分裂，枚举所有可能的分裂方案，就和CART中回归树进行划分一样，要枚举所有特征和特征的取值。该算法称为Exact Greedy Algorithm，如下图所示：

Exact Greedy Algorithm的复杂度：

设树的高度为H，特征数d，则复杂度为 O(Hdnlogn)。 其中，排序为O(nlogn)，每个特征都要排序所以乘以d，每一层都要这样一遍，所以乘以高度H（每一层第一次分裂就已经对特征的信息增益排序好了，同层的后续分类直接用排序信息就可以直接检索特征进行分裂）

证明O(nlogn)

决策树是一棵二叉树，每个叶子节点表示元素之间的一组可能排序。若决策树的深度为d，则这棵树最多有$2^d$个叶子节点，相反地，如果L个叶子节点的决策树，他的深度至少是$lo{g}_{2}L$( $2^T\ge L$)

所以，对n个元素排序的决策树必然有n!片树叶（因为n个数有n!种不同的大小关系），所以决策树的深度至少是log(n!)，即至少需要log(n!)次比较

而
$$\begin{array}{rl}log(n!)& =logn+log(n-1)+log(n-2)+...log2+log1\\ & \ge logn+log(n-1)+log(n-2)+...+log(n/2)\\ & \ge (n/2)log(n/2)(忽略常数)\\ & =O(nlogn)\end{array}$$

停止生长

一棵树不会一直生长下去，下面是一些常见的限制条件。

(1) 当新引入的一次分裂所带来的增益Gain<0时，放弃当前的分裂。这是训练损失和模型结构复杂度的博弈过程。

(2) 当树达到最大深度时，停止建树，因为树的深度太深容易出现过拟合，这里需要设置一个超参数max_depth。

(3) 当引入一次分裂后，重新计算新生成的左、右两个叶子结点的样本权重和。如果任一个叶子结点的样本权重低于某一个阈值，也会放弃此次分裂。这涉及到一个超参数:最小样本权重和，是指如果一个叶子节点包含的样本数量太少也会放弃分裂，防止树分的太细，这也是过拟合的一种措施。

每个叶子结点的样本权值和计算方式如下：$w_j=-\frac{b}{2a}=-\frac{G_j}{H_j+\lambda },则此时目标函数取到最小值$

XGBoost的一些trick

步长 step-size

XGBoost也可以加入步长η（有的也叫收缩率Shrinkage），通常步长 η 取值为0.1，这也是防止过拟合的好方法：

${\hat{y}}_i^t={\hat{y}}_i^{(t-1)}+\eta f_t\left(x_i\right)$

行列抽样

XGBoost借鉴随机森林也使用了列抽样(在每一次分裂中使用特征抽样)，进一步防止过拟合，并加速训练和预测过程。此外，在实现中还有行抽样（样本抽样）

树节点划分算法 - Approximate Algorithm

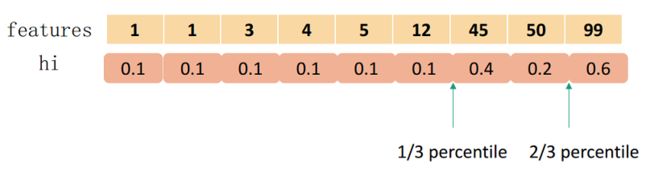
当数据量十分庞大，以致于不能全部放入内存时，Exact Greedy 算法就会很慢。因此XGBoost引入了近似的算法。简单的说，就是根据特征k的分布来确定l个候选切分点$S_k=s_{k1},s_{k2},...,s_{kl}$，然后根据这些候选切分点把相应的样本放入对应的桶中，对每个桶的G,H进行累加。最后在候选切分点集合上贪心查找，和Exact Greedy Algorithm类似。该算法描述如下：

给定了候选切分点后，一个例子为：

那么，现在有两个问题：

1. 如何选取候选切分点$S_k=s_{k1},s_{k2},...,s_{kl}$呢？
2. 什么时候进行候选切分点的选取？

切分点的选取 - Weighted Quantile Sketch

基于此，XGBoost提出了一系列加快寻找最佳分裂点的方案：

• **特征预排序+缓存+并行查找：**XGBoost在训练之前，预先对每个特征按照特征值大小（排序依据：hi）进行排序，然后保存为block结构，后面的迭代中会重复地使用这个结构，使计算量大大减小。XGBoost支持利用多个线程并行地计算每个特征的最佳分割点，这不仅大大提升了结点的分裂速度，也极利于大规模训练集的适应性扩展。
• **分位点近似法：**对每个特征按照特征值排序后，采用类似分位点选取的方式，仅仅选出常数个特征值作为该特征的候选分割点，在寻找该特征的最佳分割点时，从候选分割点中选出最优的一个。

分位数（先把数值进行排序，然后根据你采用的几分位数把数据分为几份即可）：即把概率分布划分为连续的区间，每个区间的概率相同。

以统计学常见的四分位数为例：

• 第一四分位数(Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字；
• 第二四分位数(Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字；
• 第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

而XGBoost不单单是采用简单的分位数的方法，而是对分位数进行加权（使用二阶梯度h），称为：Weighted Quantile Sketch。PS:上面的那个例子采用的是没有使用二阶导加权的分位数。

对特征k构造multi-set 的数据集：$D_k=(x_{1k},h_1),(x_{2k},h_2),...,(x_{nk}，h_n)$, 其中 $x_{ik}$表示样本i的特征k的取值，而$h_i$则为对应的二阶梯度。

可以定义一个rank function为：

$r_k(z)=\frac{1}{{\sum }_{(x,h)\in D_k}h}{\sum }_{(x,h)\in D_k,x<z}h$

rank function表达了第 $k$ 个特征小于z的样本比例，和之前的分位数挺相似，不过这里是按照二阶梯度进行累计。而候选切分点 $\left\{s_{k1},s_{k2},\cdots ,s_{kl}\right\}$ 要求:
$$||r_k\left(s_{k,j}\right)-r_k\left(s_{k,j+1}\right)\mid <\epsilon ,s_{k1}=\underset{i}{\min }{x}_{ik},s_{kl}=\underset{i}{\max }{x}_{ik}$$
用大白话说就是让相邻两个候选分裂点相差不超过某个值ε。因此，总共会得到1/ε个切分点。

一个例子如下：

要切分为3个，总和为1.8，因此第1个在0.6处，第2个在1.2处。

那么，为什么要用二阶梯度加权？将前面我们泰勒二阶展开后的目标函数2-4进行配方：

$\begin{array}{rl}& \sum _{i=1}^N\left(g_i{f}_t\left({\mathbf{x}}_{\mathbf{i}}\right)+\frac{1}{2}{h}_i{f}_t^2\left({\mathbf{x}}_{\mathbf{i}}\right)\right)+\Omega \left(f_t\right)\\ =& \sum _{i=1}^N\frac{1}{2}{h}_i\left(2\frac{g_i}{h_i}{f}_t\left({\mathbf{x}}_{\mathbf{i}}\right)+f_t^2\left({\mathbf{x}}_{\mathbf{i}}\right)\right)+\Omega \left(f_t\right)\\ =& \sum _{i=1}^N\frac{1}{2}{h}_i\left(\frac{g_i^2}{h_i^2}+2\frac{g_i}{h_i}{f}_t\left({\mathbf{x}}_{\mathbf{i}}\right)+f_t^2\left({\mathbf{x}}_{\mathbf{i}}\right)\right)+\Omega \left(f_t\right)\\ =& \sum _{i=1}^N\frac{1}{2}{h}_i{\left(f_t\left({\mathbf{x}}_{\mathbf{i}}\right)-\left(-\frac{g_i}{h_i}\right)\right)}^2+\Omega \left(f_t\right)\end{array}$

注释：

推导第三行可以加入$\frac{g_i^2}{h_i^2}$是因为$g_i$和$h_i$是上一轮的损失函数求导，是常量。上式就像是标签为$-\frac{g_i}{h_i}$，权重为$h_i$的平方损失.在建立第i棵树的时候已经知道数据集在前面i−1棵树的误差，因此采样的时候是需要考虑误差，对于误差大的特征值采样粒度要加大，误差小的特征值采样粒度可以减小，也就是说采样的样本是需要权重的。

采样粒度加大是指在抽样或数据采集过程中，选择的数据间隔变得更小，即每次采样包括的数据范围更小。在机器学习和数据处理领域，这通常意味着用于训练模型的数据点之间的距离减小了（要保证每个分位点之间的差值一样）。如果我们将数据想象成一个连续的序列，较大的采样粒度意味着我们从这个序列中选择点的步长更小。

XGBoost中，对于误差较大的特征值，增加采样粒度可以帮助模型更加集中于这些区域的重要变化，从而可能提高模型对这些区域的学习和泛化能力。

二阶导数h为权重的解释

如果损失函数是Square loss，即$Loss(y,\hat{y})=(y-\hat{y}{)}^2$，则h=2，那么实际上是不带权。 如果损失函数是Log loss，则h=pred∗(1−pred). 这是个开口朝下的一元二次函数，所以最大值在0.5。当pred在0.5附近，这个值是非常不稳定的，很容易误判，h作为权重则因此变大，那么直方图划分，这部分就会被切分的更细。

注解：

分界点选取时机

XGBoost有两种策略，全局策略（Global）和局部策略(Local)

• Global： 学习每棵树前， 即开始之前为整颗树做一次提取即可，在每次的节点划分时都使用已经提取好的候选切分点

• Local： 每次分裂前， local方式是在每次节点切分时才进行，需要很多次的提取

  注释：

  global方式需要更多的候选点，即对候选点提取数量比local更多，因为没有像local方式一样每次节点划分时(前面父节点划分过的可以不用考虑），对当前节点的样本进行细化，local方式更适合树深度较大的情况。

稀疏值处理 - Sparsity-aware Split Finding

在真实世界中，我们的特征往往是稀疏的，可能的原因有：

1. 数据缺失值；
2. 大量的0值（比如统计出现的）；
3. 进行了One-hot 编码。

XGBoost能对缺失值自动进行处理，其思想是对于缺失值自动学习出它该被划分的方向（左子树or右子树）:

注意:

上述的算法只遍历非缺失值(缺失值只是确实特征值，label是不会缺失的，不影响叶子节点的值，该值可能是该叶子节点的所有样本的label值的均值，也就不影响后面计算一阶导和二阶导)。划分的方向怎么学呢？很naive但是很有效的方法：

1. 让特征k的所有缺失值的都到右子树，然后和之前的一样，枚举划分点，计算最大的gain;
2. 让特征k的所有缺失值的都到左子树，然后和之前的一样，枚举划分点，计算最大的gain.

这样最后求出最大增益的同时，也知道了缺失值的样本应该往左边还是往右边。使用了该方法，相当于比传统方法多遍历了一次，但是它只在非缺失值的样本上进行迭代，因此其复杂度与非缺失值的样本成线性关系.

分块并行 - Column Block for Parallel Learning

在建树的过程中，最耗时是找最优的切分点，而这个过程中，最耗时的部分是将数据排序。为了减少排序的时间，提出Block结构存储数据。

• Block中的数据以稀疏格式CSC进行存储

  介绍稀疏格式CSC：

  CSC格式通常包含三个主要数组：

  1. 数值数组 (Values)：存储所有非零元素的数值，按列顺序排列。
  2. 行索引数组 (Row Indices)：存储每个非零元素的行索引。这个数组的长度与数值数组相同。
  3. 列指针数组 (Column Pointers)：存储每列非零元素在数值数组中的开始位置。此外，最后一个元素是非零元素的总数。

  假设我们有以下 4×4稀疏矩阵：

  [ 10 0 0 0 0 20 0 0 0 0 30 0 0 40 0 50 ] \left[\begin{array}{cccc}10 & 0 & 0 & 0 \\ 0 & 20 & 0 & 0 \\ 0 & 0 & 30 & 0 \\ 0 & 40 & 0 & 50\end{array}\right] ​10000​020040​00300​00050​ ​

  在CSC格式中，这个矩阵将被存储为：

  • 数值数组：10,20,40,30,50
  • 行索引数组：0,1,3,2,3（从0开始索引）
  • 列指针数组：0,1,3,4,5（第二列中有两个元素20、40，第一个元素20在数值数组中的开始位置索引是1，只记录开始位置，40的索引可以不记录）

• Block中的特征进行排序（不对缺失值排序）

• Block 中特征还需存储指向样本的索引，这样才能根据特征的值来取梯度。

• 一个Block中存储一个或多个特征的值

注意：

可以看出，只需在建树前排序一次，后面节点分裂时可以直接根据索引得到梯度信息。

• 在Exact greedy算法中，将整个数据集存放在一个Block中。这样，复杂度从原来的$O(Hd||x|{|}_{0}logn)$降为$O(Hd||x|{|}_0+||x|{|}_{0}logn)$，其中$||x|{|}_0$为训练集中非缺失值的个数。这样，Exact greedy算法就省去了每一步中的排序开销。

  分析：

  原始的稀疏贪心算法不使用块存储。因此，为了找到每个节点的最优分割，你需要在每一列上重新排序数据。这样在每一层会产生一个时间复杂度，可以非常粗略地近似为 $O\left(\Vert x{\Vert }_0\log n\right)$ : 比方说你有 $\Vert x{\Vert }_{0i}$ 个非零条目对于每一个特征 $1\le i\le m$ ； 然后在每一层你都在排序列表，每个列表最多有 $n$ 个长度，这些列表的长度总和为 ${\sum }_{i=1}^m\Vert x{\Vert }_{0i}=\Vert x{\Vert }_0$ ，排序时间不会超过 $O\left(\Vert x{\Vert }_0\log n\right)$ 。乘以 $K$ 棵树和每棵树 $d$ 层，就得到了原始的 $O\left(Kd\Vert x{\Vert }_0\log n\right)$ 时间复杂度。

  $$\begin{array}{rl}& 对所有特征进行排序的时间复杂度:\\ \sum _{i=1}^{m}log(n!)& =\sum _{i=1}^m[logn+log(n-1)+log(n-2)+...log2+log1]\\ & \ge \sum _{i=1}^m[logn+log(n-1)+log(n-2)+...+log(n-||x|{|}_{oi}+1)]\\ & \ge \sum _{i=1}^m(||x|{|}_{0i})log(n-||x|{|}_{oi}+1)(忽略常数)\\ & =O(||x|{|}_{0}logn)\end{array}$$

  另一方面，使用块结构，因为数据已经预先按照每一列排序了，所以你不需要在每个节点重新排序，只要你在每个节点(余下哪些特征)跟踪哪些特征到达了那个节点。正如作者所指出的，这将复杂度降低到 $O(Kd||x|{|}_0)$（因为现在可以通过在块上单次扫描找到每一层的最优分割,所有特征进行排序结果都实现存储在block中，只需根据csc格式索引来读取信息，需要将行索引和列索引结合与稀疏数组进行比对，数值数组、行索引和列索引中最多的数组是$||x|{|}_0$个元素）加上任何预处理的成本（作者声称这是 $O(||x|{|}_{0}logn)$，这是有意义的）。

• 在近似算法中，使用多个Block，每个Block（一个Block中存储一个或多个特征的值）对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效，因为Local策略每次分支都重新生成候选切分点。

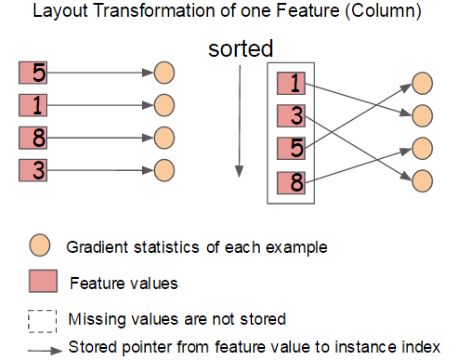
  在树生成过程中，需要花费大量的时间在特征选择与切分点选择上，并且这部分时间中大部分又花费在了对特征值得排序上。那么怎么样减小这个排序时间开销呢？

  作者提出通过按特征进行分块并排序，在块里面保存排序后的特征值及对应样本的引用，以便于获取样本的一阶、二阶导数值。具体方式如图：

  

  通过顺序访问排序后的块，遍历样本特征的特征值，方便进行切分点的查找。此外分块存储后多个特征之间互不干涉，可以使用多线程同时对不同的特征进行切分点查找，即特征的并行化处理。注意到，在顺序访问特征值时，访问的是一块连续的内存空间，但通过特征值持有的索引（样本索引）访问样本获取一阶、二阶导数时，这个访问操作访问的内存空间并不连续(左图是左边第一个对应右边，而右图第一个箭头并不是指向右边第一个），这样可能造成cpu缓存命中率低，影响算法效率。那么怎么解决这个问题呢？

  解释不连续的内存访问？

  不连续的内存访问，也称为非顺序或随机内存访问，是指对计算机内存的访问模式，其中数据访问的位置在内存中不是按照连续的、顺序的方式进行的。这与连续的内存访问形成对比，连续访问是指数据被顺序地、一个接一个地存储和访问。以下是一些详细解释：

  1. 连续内存访问：在连续的内存访问中，数据元素被顺序地存储在内存中。例如，在处理数组时，数组的元素通常存储在连续的内存位置中。当程序访问数组的一个元素后，下一个被访问的元素就是物理上紧接着的那个。这种访问模式对CPU缓存非常友好，因为一次内存读取可以将多个连续的数据元素带入缓存。
  2. 不连续内存访问：在不连续的内存访问中，数据元素在内存中的位置是分散的。例如，在处理链表或者跳跃访问数组时，接下来要访问的数据元素可能位于内存中完全不同的位置。这种访问模式对CPU缓存不友好，因为缓存无法有效地预加载即将访问的数据，导致缓存未命中的概率增加。
  3. 对CPU缓存的影响：多数现代CPU都采用某种形式的预取策略，即基于当前访问的数据来预测下一次可能访问的数据。在连续内存访问模式中，预取器可以轻松预测下一个数据块的位置，因为它通常紧随当前数据块。然而，在不连续内存访问中，下一个数据块的位置可能随机分散在内存中，使得预取变得复杂和不可靠。
  4. 缓存行和内存块：CPU缓存以缓存行的形式工作，通常一次加载整个缓存行的数据。在连续内存访问中，一次缓存行加载可能包含多个即将被访问的数据项。但在不连续访问中，加载的缓存行可能只包含单个有用数据项，其余部分可能无关或不会被立即访问。
  5. 缓存未命中的开销：每当CPU尝试从缓存中读取数据但未找到时，就会发生缓存未命中。这迫使CPU等待较慢的主内存加载数据，从而增加了延迟并降低了性能。

  xgboost中 会存在cpu缓存命中率低的原因：

  1. 特征和数据集的大小：处理具有大量特征的大型数据集时，数据量可能远远超出CPU缓存的容量，导致高缓存低命中率（缓存放不下这么多数据）。特别是在并行处理特征时，每个核心可能需要访问不同的数据集部分，这进一步增加了缓存未命中的可能性。
  2. 大量数据访问和不规则内存访问模式：XGBoost在训练过程中需要处理大量数据。特别是在并行计算特征分割点时，算法会访问大量分散在内存中的数据点。由于数据访问模式可能是不规则的（即不连续的内存访问），这可能导致CPU缓存命中率低。
  3. 计算与内存访问的比例：在XGBoost的训练过程中，计算与内存访问的比例可能导致缓存效率问题。如果算法的计算强度较低（即每次内存访问所进行的计算较少），则更多的时间会花在等待数据从内存加载到CPU上，而不是进行实际的计算。这会增加缓存未命中的机会

Block结构还有其它好处，数据按列存储，可以同时访问所有的列，很容易实现并行的寻找分裂点算法。此外也可以方便实现之后要讲的out-of score计算。

缓存优化 - Cache-aware Access

使用Block结构的一个缺点是取梯度的时候，是通过索引来获取的，而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问，可能使得CPU cache缓存命中率低，从而影响算法效率。

因此，对于exact greedy算法中, 使用缓存预取。具体来说，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式在训练样本数大的时候特别有用。

在approximate 算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的，设置过大则容易导致命中率低，过小则容易导致并行化效率不高

核外计算 Blocks for Out-of-core Computation

XGBoost的其中一个目标是，充分利用机器资源来达到scalable learning。除了处理器和内存外，很重要的一点是，使用磁盘空间来处理不能完全装载进主存的数据。当数据量太大不能全部放入主内存的时候，为了使得out-of-core计算称为可能，将数据划分为多个Block并存放在磁盘上。计算的时候，使用独立的线程预先将Block放入主内存，因此可以在计算的同时读取磁盘。但是由于磁盘IO速度太慢，通常跟不上计算的速度。因此，减小开销和增加磁盘IO吞吐很重要，Xgboost采用了2个策略：

• Block压缩（Block Compression）：将Block按列压缩，读取的时候用另外的线程解压。对于行索引，只保存第一个索引值，然后只保存该数据与第一个索引值之差(offset)，一共用16个bits来保存offset，因此，一个block一般有2的16次方个样本。

解释一个block一般有2的16次方个样本？

1. 16位二进制数的表示范围：一个二进制位（bit）可以表示两个值（0或1）。因此，16位二进制数可以表示的不同值的数量是 $2^{16}$，即65536。这是因为每增加一个比特，表示的值的数量就翻倍。
2. 偏移量的存储：在这种方法中，每个行索引的偏移量被限制为16位，这意味着每个偏移量可以表示从0到65535的范围（最大的偏移量为65535，也就是$2^{16}+0(第一个元素的索引为0)$）。这些偏移量是相对于第一个索引值的，所以偏移量0表示第一个索引本身。

• Block拆分（Block Sharding）：将数据划分到不同磁盘上，为每个磁盘分配一个**预取（pre-fetcher）**线程，并将数据提取到内存缓冲区中。然后，训练线程交替地从每个缓冲区读取数据。这有助于在多个磁盘可用时增加磁盘读取的吞吐量。

总结

读到这里，相信你对XGBoost已经很有了解。下面总结几个问题：

XGBoost为什么快

• 当数据集大的时候使用近似算法
• Block与并行
• CPU cache 命中优化
• Block预取、Block压缩、Block Sharding等

XGBoost与传统GBDT的不同

• 传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。

• 传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导。

• xgboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是xgboost优于传统GBDT的一个特性。

• Shrinkage（缩减），相当于学习速率（xgboost中的eta）。xgboost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）

• 列抽样（column subsampling）。xgboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。

• 对缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。

• xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

  特征的粒度：在机器学习中，特征是数据集中的属性或变量，用于描述每个样本的不同方面。例如，在房价预测问题中，特征可以包括房子的面积、卧室数量、浴室数量等。这些特征是用来训练和测试机器学习模型的输入。

  在特征的粒度上的并行：XGBoost中的并行计算是针对每个特征的。具体来说，XGBoost可以同时处理数据集中的不同特征，而不是按照顺序逐个处理。这意味着在训练或预测时，XGBoost可以并行计算每个特征的信息增益（或梯度），然后将这些结果合并以更新模型的状态。这种特征级别的并行计算使XGBoost能够高效地处理大量特征，尤其是在大规模数据集上。

• 可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

XGBoost Scalable的体现

XGBoost的paper在KKD上发表，名为：《Xgboost: A scalable tree boosting system》，那么scalable体现在哪?

• 模型的scalability：弱分类器可以支持cart也可以支持lr和linear， 但其实这是Boosting算法做的事情，XGBoost只是实现了而已。
• 目标函数的scalability： 支持不同的loss function, 支持自定义loss function，只要一、二阶可导。有这个特性是因为泰勒二阶展开，得到通用的目标函数形式。
• 学习方法的scalability：Block结构支持并行化，支持 Out-of-core计算

XGBoost 防止过拟合的方法

• 目标函数的正则项， 叶子节点数+叶子节点数输出分数的平方和 $\Omega \left(f_t\right)=\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_j^2$
• 行抽样和列抽样：训练的时候只用一部分样本和一部分特征
• 可以设置树的最大深度
• η: 可以叫学习率、步长或者shrinkage
• Early stopping：使用的模型不一定是最终的ensemble，可以根据测试集的测试情况，选择使用前若干棵树

XGBoost的创新点

• 第一，实现精确性与复杂度之间的平衡

树的集成模型是机器学习中最为强大的学习器之一，这一族学习器的特点是精确性好、适用于各种场景，但运行缓慢、且过拟合风险很高，而剪枝策略的目的就是为了降低各种树模型的模型复杂度，从而控制住过拟合。树模型的学习能力与过拟合风险之间的平衡，就是预测精确性与模型复杂度之间的平衡，也是经验风险与结构风险之间的平衡，这一平衡对决策树以及树的集成模型来说是永恒的议题。

在过去，我们总是先建立效果优异的模型，再依赖于手动剪枝来调节树模型的复杂度，但在XGBoost中，精确性与复杂度会在训练的每一步被考虑到。主要体现在：

• 1. XGBoost为损失函数$L(y,\hat{y})$加入结构风险项，构成目标函数$O(y,\hat{y})$

  在AdaBoost与GBDT当中，我们的目标是找到损失函数$L(y,\hat{y})$的最小值，也就是让预测结果与真实结果差异最小，这一流程只关心精确性、不关心复杂度和过拟合情况。为应对这个问题，XGBoost从决策树的预剪枝流程、逻辑回归、岭回归、Lasso等经典算法的抗过拟合流程吸取经验，在损失函数中加入了控制过拟合的结构风险项，并将【$L(y,\hat{y})$ + 结构风险】定义为目标函数$O(y,\hat{y})$。

  这一变化让XGBoost在许多方面都与其他Boosting算法不同：例如，XGBoost是向着令目标函数最小化的目标进行训练，而不是令损失函数最小化的方向。再比如，XGBoost会优先利用结构风险中的参数来控制过拟合，而不像其他树的集成模型一样依赖于树结构参数（例如max_depth，min_impurity_decrease等）。

• 2. 使用全新不纯度衡量指标，将复杂度纳入分枝规则

  在之前学过的算法当中，无论Boosting流程如何进化，建立单棵决策树的规则基本都遵循我们曾经学过的CART树流程，在分类树中，我们使用信息增益（information gain）来衡量叶子的质量，在回归树中，我们使用MSE或者弗里德曼MSE来衡量叶子的质量。这一流程有成熟的剪枝机制、预测精度高、能够适应各种场景，但却可能建立复杂度很高的树。

  为实现精确性与复杂度之间的平衡，XGBoost重新设定了分枝指标**【结构分数】（原论文中写作Structure Score，也被称为质量分数Quality Score），以及基于结构分数的【结构分数增益】**（Gain of structure score），结构分数增益可以逼迫决策树向整体结构更简单的方向生长。

  这一变化让XGBoost使用与传统CART略有区别的建树流程，同时在建树过程中大量使用残差（Residuals）或类残差对象作为中间变量，因此XGBoost的数学过程比其他Boosting算法更复杂。

• 第二，极大程度地降低模型复杂度、提升模型运行效率，将算法武装成更加适合于大数据的算法

在任意决策树的建树过程中，都需要对每一个特征上所有潜在的分枝节点进行不纯度计算，当数据量巨大时，这一计算将消耗巨量的时间，因此树集成模型的关键缺点之一就是计算缓慢，而这一缺点在实际工业环境当中是相当致命的。为了提升树模型的运算速度、同时又不极大地伤害模型的精确性，XGBoost使用多种优化技巧来实现效率提升：

• 1. 使用估计贪婪算法、平行学习、分位数草图算法等方法构建了适用于大数据的全新建树流程
• 2. 使用感知缓存访问技术与核外计算技术，提升算法在硬件上的运算性能
• 3. 引入Dropout技术，为整体建树流程增加更多随机性、让算法适应更大数据
  不仅在数学方法上有所改进，XGBoost正式拉开了Boosting算法工程优化的序幕。后续更多的Boosting算法，包括LightGBM，CatBoost等也都是在工程方法上做出了大量的优化。

除此之外，XGBoost还保留了部分与梯度提升树类似的属性，包括：

• 弱评估器的输出类型与集成算法输出类型不一致

对于AdaBoost或随机森林算法来说，当集成算法执行的是回归任务时，弱评估器也是回归器，当集成算法执行分类任务时，弱评估器也是分类器。但对于GBDT以及基于GBDT的复杂Boosting算法们而言，无论集成算法整体在执行回归/分类/排序任务，弱评估器一定是回归器。GBDT通过sigmoid或softmax函数输出具体的分类结果，但实际弱评估器一定是回归器，XGBoost也是如此。

• 拟合负梯度，且当损失函数是0.5倍MSE时，拟合残差

任意Boosting算法都有自适应调整弱评估器的步骤。在GBDT当中，每次用于建立弱评估器的是样本$X$以及当下集成输出$H(x_i)$与真实标签$y$之间的伪残差（也就是负梯度）。当损失函数是$\frac{1}{2}MSE$时，负梯度在数学上等同于残差（Residual），因此GBDT是通过拟合残差来影响后续弱评估器结构。XGBoost也是依赖于拟合残差来影响后续弱评估器结构，但是与GBDT一样，这一点需要通过数学来证明。

• 抽样思想

GBDT借鉴了大量Bagging算法中的抽样思想，XGBoost也继承了这一属性，因此在XGBoost当中，我们也可以对样本和特征进行抽样来增大弱评估器之间的独立性

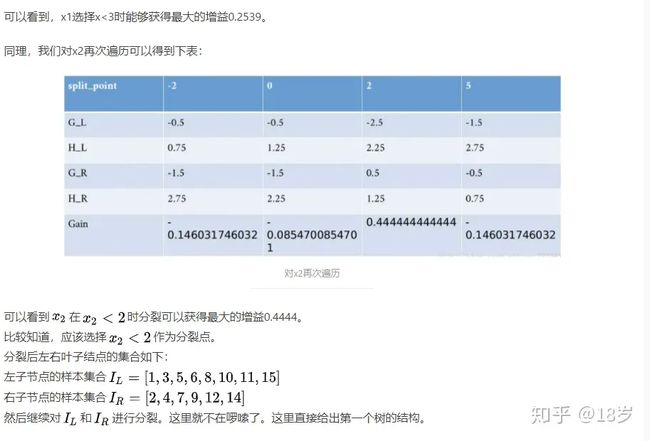
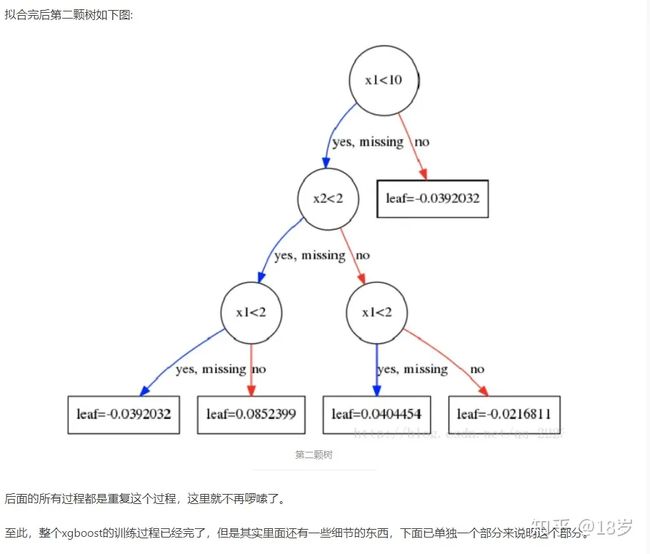
XGBoost实例（copy的知乎的一个例子，目的是熟悉算法流程）

注意：logloss：$y_{i}log(1+e^{-{\hat{y}}_i})+(1-y_i)\ast log(1+e^{{\hat{y}}_i}))$（下面图片的中$L(y_i,{\hat{y}}_i)$错了)

相比于GBDT，XGBoost的优点？

解释：XGBoost拟合的也是残差?

当目标函数为$\frac{1}{2}MSE$，负梯度$-g_i$就等于残差，而$h_i=1$，因此拟合项$-\frac{g_i}{h_i}$自然也是残差本身了。因此，XGBoost也是拟合负梯度的算法，并且在特定损失函数下，XGBoost也拟合残差。

---

参考资料

1. https://www.matongxue.com/madocs/7/
2. https://www.matongxue.com/madocs/126/
3. 菜菜九天机器学习课程
4. https://www.hrwhisper.me/machine-learning-xgboost/
5. Chen, Tianqi, and Carlos Guestrin. “Xgboost: A scalable tree boosting system.” Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. ACM, 2016.
6. https://zhuanlan.zhihu.com/p/92837676
7. http://t.csdnimg.cn/mTL0h
8. XGBoost 与 Boosted Tree - 陈天奇：https://pan.baidu.com/s/10NWfRM9qimswGxPsF9VlDw 密码:v3y6