算法与数据结构之数组轮转问题详解｜力扣leetcode189（cpp、Java实现）超级详细！！！

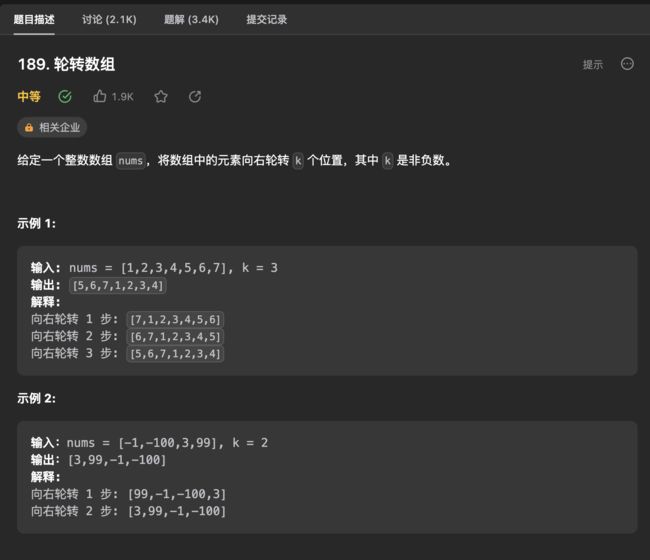
189 轮转数组

数组轮转问题

力扣

方法一：分组翻转

先将整个数组翻转，然后再将前k个元素翻转，再将剩余的n-k个元素翻转。时间复杂度为O(n)，空间复杂度为O(1)。

下面是CPP的实现代码:

class Solution {
public:
    void rotate(vector& nums, int k) {
        k=k%nums.size();
        reverse(nums,0,nums.size()-1);
        reverse(nums,0,k-1);
        reverse(nums,k,nums.size()-1);
    }
    void reverse(vector& nums, int start, int end){
        while(start

cpp中可以利用专门的颠倒顺序的函数reverse实现。从而达到简化代码的效果：

class Solution {
public:
    void rotate(vector& nums, int k) {
        int n = nums.size();
        k %= n;
        reverse(nums.begin(), nums.end());
        reverse(nums.begin(), nums.begin() + k);
        reverse(nums.begin() + k, nums.end());
    }
};

这种方法优化了内存，但是折损了时间。

下面是C语言的实现代码:

void rotate(int* nums, int numsSize, int k) {
    k %= numsSize;
    reverse(nums, 0, numsSize - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, numsSize - 1);
}

void reverse(int* nums, int start, int end) {
    while (start < end) {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start += 1;
        end -= 1;
    }
}

需要注意的：

C语言中并没有直接获取数组长度的函数，需要使用一些技巧计算数组长度。

一种方法是通过 sizeof 操作符计算数组的字节数，然后除以单个元素的字节数得到数组长度。

例如，对于一个 int 类型的数组 arr，可以使用下面的语句计算数组长度：

int arr[] = {1, 2, 3, 4, 5};
int arr_len = sizeof(arr) / sizeof(int);

另一种方法是在定义数组时，同时记录数组长度。例如：

int arr[] = {1, 2, 3, 4, 5};
int arr_len = 5;

这种方法在计算数组长度时更加直观，但需要手动更新数组长度，不如第一种方法灵活。

下面是Java的实现代码:

class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;//这一行必不可少，为什么
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }
    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start += 1;
            end -= 1;
        }
    }
}

• k %= nums.length;的作用是什么？

答：

题目中并没有说明k的取值小于数组长度。

在这个代码中，k %= nums.length; 的作用是将k对数组长度取模，确保k的值在合法范围内。

如果没有这一行，当k大于数组长度时，会导致数组的翻转不完整，从而出现错误的结果。

例如，如果数组长度为5，k的值为8，那么没有这一行的话，经过翻转操作后，数组的前3个元素会被正确翻转，但是剩余的2个元素则没有执行翻转操作。这样就会导致最终结果不正确。

通过取模运算，k %= nums.length; 将k的值限制在数组长度范围内，这样就能确保完整的数组翻转操作，从而得到正确的结果。

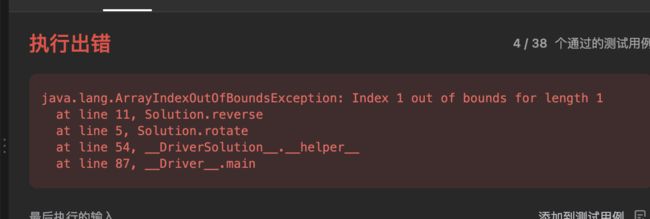
否则，k 太大会越界，从而出现以下报错：java.lang.IndexOutOfBoundsException: Index 1 out of bounds for length 1（如图）

这个错误是由于在Java代码中尝试访问数组或列表等数据结构的越界索引导致的。当你试图访问一个超出其有效长度的索引时，就会出现这个错误。

方法二：使用额外的数组

将原数组的元素根据旋转规则依次放入新数组的对应位置。然后将新数组复制回原数组即可。时间复杂度为O(n)，空间复杂度为O(n)。

下面是CPP的实现代码:

class Solution {
public:
    void rotate(vector& nums, int k) {
        int n = nums.size();
        vector temp(n);
        for (int i = 0; i < n; i++) {
            temp[(i + k) % n] = nums[i];//将原数组下标为i的元素放至新数组下标为(i+k)%n的位置
        }
        nums = temp;
    }
};

下面是Java的实现代码:

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] temp = new int[n];
        for (int i = 0; i < n; i++) {
            temp[(i + k) % n] = nums[i];
        }
        System.arraycopy(temp, 0, nums, 0, n);//将 temp 数组中的前 n 个元素复制到 nums 数组中的起始位置。
    }
}

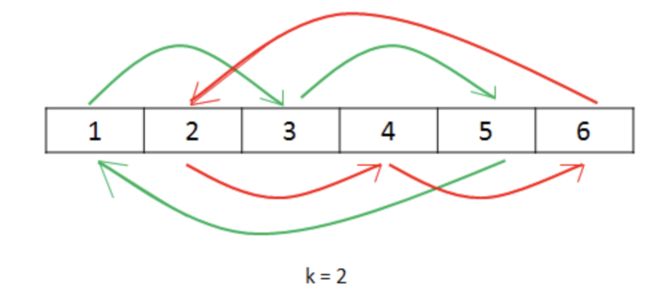
方法三：环状替换

通过从某个位置开始进行元素的交换，每次移动到下一个位置，直到回到起始位置。时间复杂度为O(n)，空间复杂度为O(1)。

cpp实现方式：

class Solution {
public:
    void rotate(vector& nums, int k) {
        int n = nums.size();
        k %= n;
        int count = gcd(k, n);
        for (int start = 0; start < count; start++) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % n;
                swap(nums[next], prev);
                current = next;
            } while (start != current);
        }
    }
};

gcd函数的作用是求最大公约数（Greatest Common Divisor，简称gcd）。

Java实现方式：

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n;
        int count = gcd(k, n);
        for (int start = 0; start < count; start++) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % n;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
            } while (start != current);
        }
    }
    public int gcd(int x, int y) {
        return y > 0 ? gcd(y, x % y) : x;
    }
}

Java中有求最大公约数（Greatest Common Divisor，简称GCD）的函数可以使用，它是Math类中的一个静态方法。具体实现如下：

public static int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

其中，a和b是要想求它们的最大公约数的两个整数。这个函数是使用递归方式实现的，若b等于0，则最大公约数即为a，否则，即对b和a对b所得的余数进行递归操作，直到b等于0。

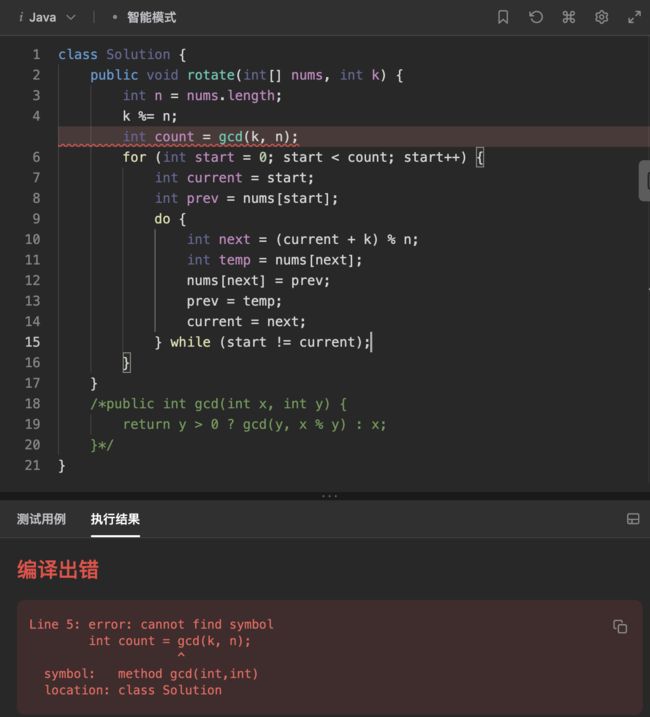
但是不单独写gcd函数的定义会报错，如下图所示：

那么，问题来了：

在Java中明明有gcd函数的定义，为什么还要另外写一遍？

因为，Java中确实有gcd函数的定义，即Math类中的静态方法gcd。但是在这个问题中，gcd方法的实现使用了递归，而Java中的Math类中的gcd函数使用了辗转相除法来实现，两者的实现方式不同。

辗转相除法是一种求最大公约数的算法，也叫欧几里得算法。其原理是：设a、b为两个整数，且a>b，a%b得余数为c，若c=0，则b即为两数的最大公约数；若c≠0，则令a=b，b=c，继续进行相除操作，直到余数为0为止。而辗转相除法的循环次数等于a和b的最大公约数，因此可以用来优化求解旋转数组问题的代码。

所以在这个问题中，使用递归实现的gcd方法就是为了用于优化旋转数组的代码，使得其能更快地求解最大公约数。

总结

解题思路：

1. 使用额外的数组：将原数组的元素根据旋转规则依次放入新数组的对应位置。然后将新数组复制回原数组即可。时间复杂度为O(n)，空间复杂度为O(n)。
2. 环状替换：通过从某个位置开始进行元素的交换，每次移动到下一个位置，直到回到起始位置。时间复杂度为O(n)，空间复杂度为O(1)。
3. 数组翻转：先将整个数组翻转，然后再将前k个元素翻转，再将剩余的n-k个元素翻转。时间复杂度为O(n)，空间复杂度为O(1)。