【学习强化学习】三、Q learning和Sarsa算法
文章目录
- 参考资料
- 1. Q- table
- 2. Model-free Prediction
-
- 2.1 Monte-Carlo Policy Evaluation
-
- 2.1.1 MC算法步骤
- 2.1.2 incremental MC updates
- 2.1.3 Difference between DP and MC for policy evaluation
- 2.1.4 Advantages of MC over DP
- 2.2 Temporal Difference
-
- 2.2.1 TD 方法介绍
- 2.2.2 Advantages of TD over MC
- 2.2.3 n-step TD
- 2.2.4 Bootstrapping and Sampling for DP,MC and TD
- 3. Model-free Control
-
- 3.1 Policy Iteration
-
- 3.1.1 Policy Iteration for a Known MDP
- 3.1.2 Generalized Policy Iteration with Action-Value Function
- 3.1.3 Monte Carlo with Exploring Starts
- 3.1.4 Monte Carlo with ε \varepsilon ε-Greedy Exploration
- 3.1.5 On Policy First Visit Monte Carlo algorithm
- 3.1.6 Off Policy Monte Carlo Algorithm
- 3.2 Sarsa: On-policy TD Control
-
- 3.2.1 sarsa 介绍
- 3.2.2 n-step Sarsa
- 3.2.3 算法伪代码
- 3.3 Q-learning: Off-policy TD Control
-
- 3.3.1 off-policy 介绍
- 3.3.2 Q-learning
- 3.3.3 算法伪代码
- 3.3.4 Q learning VS Sarsa
- 4. On-policy vs. Off-policy
- 5. 练习
-
- 5.1 简答题
-
- 5.1.1 Q表格型表示方法
- 5.1.2 时序差分(Temporal Difference)
- 5.2 问答题
-
- 5.2.1 基于SARSA算法的agent的学习过程?
- 5.2.2 能否简述on-policy和off-policy的区别?
- 5.2.3 能否讲一下Q-Learning?
- 5.2.4 能否讲一下SARSA?
- 5.2.5 请问value-based和policy-based的区别是什么?
- 5.2.6 请简述以下时序差分(Temporal Difference,TD)算法。
- 5.2.7 请问蒙特卡洛方法(Monte Carlo Algorithm,MC)和时序差分(Temporal Difference,TD)算法是无偏估计吗?
- 5.2.8 能否简单说下动态规划、蒙特卡洛和时序差分的异同点?
- 6. 编程题
-
- 6.1 使用Q-learning解决悬崖寻路问题
-
- 6.1.1 CliffWalking-v0环境简介
- 6.1.2 算法实现
- 6.2 使用Sarsa解决悬崖寻路问题
- 6.3 使用蒙特卡洛算法解决悬崖寻路问题
-
- 6.3.1 on policy first visit MC control
- 6.3.2 off policy MC control
参考资料
表格型方法
1. Q- table
-
Q table存储的是所有状态动作对的价值。其中横坐标为 action(agent)的行为,纵坐标是环境的state
-
Q表格里面 Q 函数的意义就是选择了某个动作之后,最后能不能成功,还需要去计算在当前状态下,选择了这个动作,后续能够一共拿到多少总收益。如果可以预估未来的总收益的大小,显然可以知道在当前的状态下选择哪个动作,价值更高。选择哪个动作是基于未来可以拿到的价值哪个更高一点。所以强化学习的目标导向性很强,环境给出的奖励是一个非常重要的反馈,它根据环境的奖励来去做选择。
-
Q: 为什么可以用未来的总收益来评价当前动作是好是坏?
-
A: 举个例子,假设一辆车在路上,当前是红灯,我们直接走的收益很低,因为违反交通规则,这就是当前的单步收益。可是如果是一辆救护车,我们正在运送病人,把病人快速送达医院的收益非常的高,而且越快你的收益越大。在这种情况下,我们很可能应该要闯红灯,因为未来的远期收益太高了。这也是为什么强化学习需要去学习远期的收益,因为在现实世界中奖励往往是延迟的。所以我们一般会从当前状态开始,把后续有可能会收到所有收益加起来计算当前动作的 Q 的价值,让 Q 的价值可以真正地代表当前这个状态下,动作的真正的价值。

-
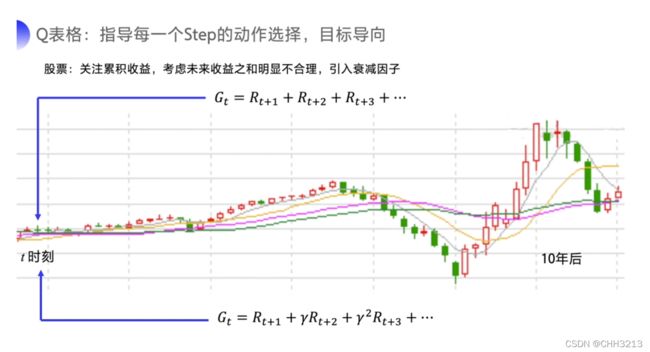
但有的时候把目光放得太长远不好,因为如果事情很快就结束的话,你考虑到最后一步的收益无可厚非。如果是一个持续的没有尽头的任务,即持续式任务(Continuing Task),你把未来的收益全部相加,作为当前的状态价值就很不合理。
-
例如股票的例子,我们要关注的是累积的收益。可是如果说十年之后才有一次大涨大跌,显然不会把十年后的收益也作为当前动作的考虑因素。我们可以引入这个衰减因子 γ \gamma γ 来去计算这个未来总收益, γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1],越往后 γ n \gamma^n γn 就会越小,也就是说越后面的收益对当前价值的影响就会越小。
-
- 类似于上图,最后我们要求解的就是一张 Q 表格, 它的行数是所有的状态数量,一般可以用坐标来表示表示格子的状态,也可以用 1、2、3、4、5、6、7 来表示不同的位置。Q 表格的列表示上下左右四个动作。
- 最开始这张 Q 表格会全部初始化为零,然后 agent 会不断地去和环境交互得到不同的轨迹,当交互的次数足够多的时候,我们就可以估算出每一个状态下,每个行动的平均总收益去更新这个 Q 表格。怎么去更新 Q 表格就是接下来要引入的强化概念。
2. Model-free Prediction
在没法获取 MDP 的模型情况下,我们可以通过以下两种方法来估计某个给定策略的价值:
- Monte Carlo policy evaluation
- Temporal Difference(TD) learning
2.1 Monte-Carlo Policy Evaluation
- 蒙特卡罗(Monte-Carlo,MC)方法是基于采样的方法,让 agent 跟环境进行交互,就会得到很多轨迹。每条轨迹都有对应的 return:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + … G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots Gt=Rt+1+γRt+2+γ2Rt+3+…
-
把每个轨迹的 return 进行平均,就可以知道某一个策略下面对应状态的价值。
-
MC 是用 经验平均回报(empirical mean return) 的方法来估计。
-
MC 方法不需要 MDP 的转移函数和奖励函数,并且不需要像动态规划那样用 bootstrapping 的方法。
-
MC 的局限性:只能用在有终止的 MDP 。
2.1.1 MC算法步骤
-
为了评估 v ( s ) v(s) v(s),需要进行如下步骤:
- 在每个回合中,如果在时间步 t 时状态 s 被访问了,那么
- 状态 s 的访问数 N ( s ) N(s) N(s) 增加 1,
- 状态 s 的总的回报 S ( s ) S(s) S(s) 增加 G t G_t Gt。
- 状态 s 的价值可以通过 return 的平均来估计,即 v ( s ) = S ( s ) / N ( s ) v(s)=S(s)/N(s) v(s)=S(s)/N(s)。
- 在每个回合中,如果在时间步 t 时状态 s 被访问了,那么
-
根据大数定律,只要我们得到足够多的轨迹,就可以趋近这个策略对应的价值函数。
2.1.2 incremental MC updates
假设现在有样本 x 1 , x 2 , ⋅ x_1,x_2,\cdot x1,x2,⋅,我们可以把经验均值(empirical mean)转换成增量均值(incremental mean) 的形式,如下式所示: μ t = 1 t ∑ j = 1 t x j = 1 t ( x t + ∑ j = 1 t − 1 x j ) = 1 t ( x t + ( t − 1 ) μ t − 1 ) = 1 t ( x t + t μ t − 1 − μ t − 1 ) = μ t − 1 + 1 t ( x t − μ t − 1 ) \begin{aligned} \mu_{t} &=\frac{1}{t} \sum_{j=1}^{t} x_{j} \\ &=\frac{1}{t}\left(x_{t}+\sum_{j=1}^{t-1} x_{j}\right) \\ &=\frac{1}{t}\left(x_{t}+(t-1) \mu_{t-1}\right) \\ &=\frac{1}{t}\left(x_{t}+t \mu_{t-1}-\mu_{t-1}\right) \\ &=\mu_{t-1}+\frac{1}{t}\left(x_{t}-\mu_{t-1}\right) \end{aligned} μt=t1j=1∑txj=t1(xt+j=1∑t−1xj)=t1(xt+(t−1)μt−1)=t1(xt+tμt−1−μt−1)=μt−1+t1(xt−μt−1)
通过这种转换,我们就可以把上一时刻的平均值跟现在时刻的平均值建立联系,即: μ t = μ t − 1 + 1 t ( x t − μ t − 1 ) \mu_t = \mu_{t-1}+\frac{1}{t}(x_t-\mu_{t-1}) μt=μt−1+t1(xt−μt−1)
其中:
x t − μ t − 1 x_t- \mu_{t-1} xt−μt−1 是残差
1 t \frac{1}{t} t1类似于学习率(learning rate)当我们得到 x t x_t xt,就可以用上一时刻的值来更新现在的值。
我们可以把 Monte-Carlo 更新的方法写成 incremental MC 的方法:
- 采集数据,得到一个新的轨迹 ( S 1 , A 1 , R 1 , . . . , S t ) (S_1,A_1,R_1,...,S_t) (S1,A1,R1,...,St)。
- 对于这个轨迹,我们采用增量的方法进行更新,如下式所示:
N ( S t ) ← N ( S t ) + 1 v ( S t ) ← v ( S t ) + 1 N ( S t ) ( G t − v ( S t ) ) \begin{array}{l} N\left(S_{t}\right) \leftarrow N\left(S_{t}\right)+1 \\ v\left(S_{t}\right) \leftarrow v\left(S_{t}\right)+\frac{1}{N\left(S_{t}\right)}\left(G_{t}-v\left(S_{t}\right)\right) \end{array} N(St)←N(St)+1v(St)←v(St)+N(St)1(Gt−v(St))
- 我们可以直接把 1 N ( S t ) \frac{1}{N(S_t)} N(St)1 变成 α \alpha α (学习率), α \alpha α 代表着更新的速率有多快,可以进行人为设置。
2.1.3 Difference between DP and MC for policy evaluation
-
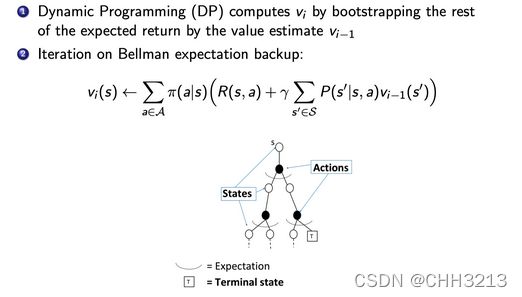
动态规划也是常用的估计价值函数的方法。在动态规划里面,我们使用了 bootstrapping 的思想。bootstrapping 的意思就是我们基于之前估计的量来估计当前的量。
-
DP 就是用 Bellman expectation backup,就是通过上一时刻的值 v i − 1 ( s ′ ) v_{i-1}(s') vi−1(s′) 来更新当前时刻 v i ( s ) v_i(s) vi(s)这个值,不停迭代,最后可以收敛。Bellman expectation backup 有两层加和,内部加和和外部加和,即算了两次 expectation。
-
MC 是通过
empirical mean return(实际得到的收益)来更新它,对应上图蓝色的轨迹,我们得到的是一个实际的轨迹,实际的轨迹上的状态已经是确定的,采取的行为都是确定的。MC 得到的是一条轨迹,这条轨迹表现出来就是这个蓝色的从起始到最后终止状态的轨迹。现在只是更新这个轨迹上的所有状态,跟这个轨迹没有关系的状态都没有更新。

2.1.4 Advantages of MC over DP
- MC 可以在不知道环境的情况下 work,而 DP 是 model-based。
- MC 只需要更新一条轨迹的状态,而 DP 则是需要更新所有的状态。状态数量很多的时候(比如一百万个,两百万个),DP 这样去迭代的话,速度是非常慢的。这也是 MC这种 sample-based 的方法 相对于 DP 的优势。
2.2 Temporal Difference
- 为了让大家更加直观感受下一个状态影响上一个状态(状态价值迭代),大家可以跳转这个网站:Temporal Difference Learning Gridworld Demo。
2.2.1 TD 方法介绍
-
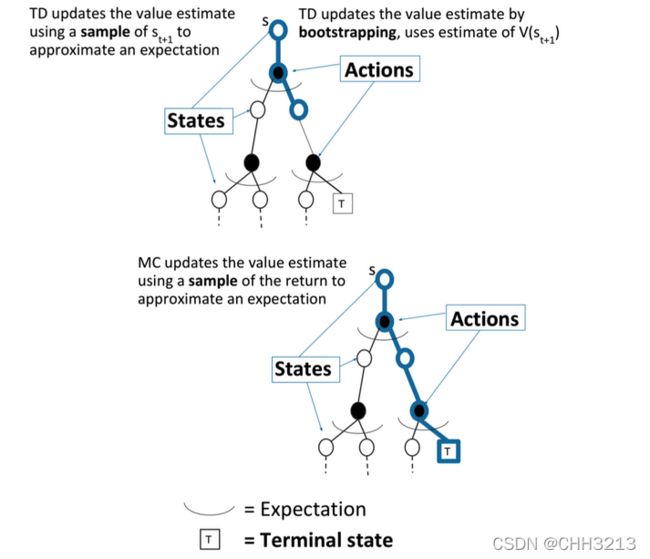
TD 是介于 MC 和 DP 之间的方法。
-
TD 是 model-free 的,不需要 MDP 的转移矩阵和奖励函数。
-
TD 可以从不完整的 episode 中学习,结合了 bootstrapping 的思想。
-
目的:对于某个给定的策略,在线(online)地算出它的价值函数,即一步一步地(step-by-step)算。
-
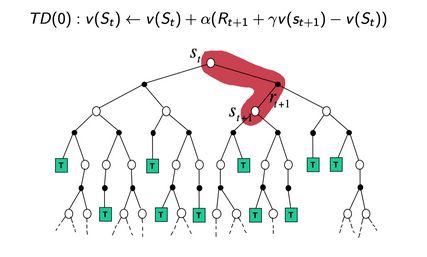
最简单的算法是 TD(0),每往前走一步,就做一步 bootstrapping,用得到的估计回报(estimated return)来更新上一时刻的值。
-
估计回报 R t + 1 + γ v ( S t + 1 ) R_{t+1}+\gamma v(S_{t+1}) Rt+1+γv(St+1) 被称为 TD target,TD target 是带衰减的未来收益的总和。TD target 由两部分组成:
- 走了某一步后得到的实际奖励: R t + 1 R_{t+1} Rt+1,
- γ v ( S t + 1 ) \gamma v(S_{t+1}) γv(St+1)是利用了 bootstrapping 的方法,通过之前的估计来估计 v ( S t + 1 ) v(S_{t+1}) v(St+1) ,然后加了一个折扣系数,具体过程如下式所示:
v ( s ) = E [ G t ∣ s t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + … ∣ s t = s ] = E [ R t + 1 ∣ s t = s ] + γ E [ R t + 2 + γ R t + 3 + γ 2 R t + 4 + … ∣ s t = s ] = R ( s ) + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ v ( s t + 1 ) ∣ s t = s ] \begin{aligned} v(s)&=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid s_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}|s_t=s\right] +\gamma \mathbb{E}\left[R_{t+2}+\gamma R_{t+3}+\gamma^{2} R_{t+4}+\ldots \mid s_{t}=s\right]\\ &=R(s)+\gamma \mathbb{E}[G_{t+1}|s_t=s] \\ &=R(s)+\gamma \mathbb{E}[v(s_{t+1})|s_t=s]\\ \end{aligned} v(s)=E[Gt∣st=s]=E[Rt+1+γRt+2+γ2Rt+3+…∣st=s]=E[Rt+1∣st=s]+γE[Rt+2+γRt+3+γ2Rt+4+…∣st=s]=R(s)+γE[Gt+1∣st=s]=R(s)+γE[v(st+1)∣st=s]
-
之所以TD target 是一个估计,是因为:它对期望值进行采样,并且使用当前估计 V 而不是真实的 v π v_{\pi} vπ。
-
TD error(误差)
δ = R t + 1 + γ v ( S t + 1 ) − v ( S t ) \delta=R_{t+1}+\gamma v(S_{t+1})-v(S_t) δ=Rt+1+γv(St+1)−v(St) -
可以类比于
Incremental Monte-Carlo的方法,写出如下的更新方法:
v ( S t ) ← v ( S t ) + α ( R t + 1 + γ v ( S t + 1 ) − v ( S t ) ) v\left(S_{t}\right) \leftarrow v\left(S_{t}\right)+\alpha\left(R_{t+1}+\gamma v\left(S_{t+1}\right)-v\left(S_{t}\right)\right) v(St)←v(St)+α(Rt+1+γv(St+1)−v(St))
- 通过上式与MC的更新式子对比,我们可知:
v ( S t ) ← v ( S t ) + α ( G i , t − v ( S t ) ) \begin{array}{l}v\left(S_{t}\right) \leftarrow v\left(S_{t}\right)+\alpha\left(G_{i,t}-v\left(S_{t}\right)\right) \end{array} v(St)←v(St)+α(Gi,t−v(St))- 在 MC 里面 G i , t G_{i,t} Gi,t 是实际得到的值(可以看成 target),因为它已经把一条轨迹跑完了,可以算每个状态实际的 return。
- TD 没有等轨迹结束,往前走了一步,就可以更新价值函数。
2.2.2 Advantages of TD over MC
-
TD 只执行了一步,状态的值就更新。
-
MC 全部走完了之后,到了终止状态之后,再更新它的值。
-
TD 可以在线学习(online learning),每走一步就可以更新,效率高。
-
MC 必须等一个回合结束才可以学习。
-
TD 可以从不完整序列上进行学习。
-
MC 只能从完整的序列上进行学习。
-
TD 可以在连续的环境下(没有终止)进行学习。
-
MC 只能在有终止的情况下学习。
-
TD 利用了马尔可夫性质,在马尔可夫环境下有更高的学习效率。
-
MC 没有假设环境具有马尔可夫性质,利用采样的价值来估计某一个状态的价值,在不是马尔可夫的环境下更加有效。
-
举个例子来解释 TD 和 MC 的区别,
-
TD 是指在不清楚马尔可夫状态转移概率的情况下,以采样的方式得到不完整的状态序列,估计某状态在该状态序列完整后可能得到的收益,并通过不断地采样持续更新价值。
-
MC 则需要经历完整的状态序列后,再来更新状态的真实价值。
-
例如,你想获得开车去公司的时间,每天上班开车的经历就是一次采样。假设今天在路口 A 遇到了堵车,
- TD 会在路口 A 就开始更新预计到达路口 B、路口 C ⋯ ⋯ \cdots \cdots ⋯⋯,以及到达公司的时间;
- 而 MC 并不会立即更新时间,而是在到达公司后,再修改到达每个路口和公司的时间。
-
-
TD 能够在知道结果之前就开始学习,相比 MC,其更快速、灵活。
2.2.3 n-step TD
-
我们可以把 TD 进行进一步的推广。之前是只往前走一步,即 one-step TD,TD(0)。
-
我们可以调整步数,变成 n-step TD。比如 TD(2),即往前走两步,然后利用两步得到的 return,使用 bootstrapping 来更新状态的价值。
-
这样就可以通过 step 来调整这个算法需要多少的实际奖励和 bootstrapping。
-
- 通过调整步数,可以进行一个 MC 和 TD 之间的 trade-off,如果 n = ∞ n=\infty n=∞, 即整个游戏结束过后,再进行更新,TD 就变成了 MC。
- n-step 的 TD target 如下式所示:
G t n = R t + 1 + γ R t + 2 + … + γ n − 1 R t + n + γ n v ( S t + n ) G_{t}^{n}=R_{t+1}+\gamma R_{t+2}+\ldots+\gamma^{n-1} R_{t+n}+\gamma^{n} v\left(S_{t+n}\right) Gtn=Rt+1+γRt+2+…+γn−1Rt+n+γnv(St+n) - 得到 TD target 之后,我们用增量学习(incremental learning)的方法来更新状态的价值:
v ( S t ) ← v ( S t ) + α ( G t n − v ( S t ) ) v\left(S_{t}\right) \leftarrow v\left(S_{t}\right)+\alpha\left(G_{t}^{n}-v\left(S_{t}\right)\right) v(St)←v(St)+α(Gtn−v(St))
2.2.4 Bootstrapping and Sampling for DP,MC and TD
-
Bootstrapping:更新时使用了估计:
- MC 没用 bootstrapping,因为它是根据实际的 return 来更新。
- DP 用了 bootstrapping。
- TD 用了 bootstrapping。
-
Sampling:更新时通过采样得到一个期望:
- MC 是纯 sampling 的方法。
- DP 没有用 sampling,它是直接用
Bellman expectation equation来更新状态价值的。 - TD 用了 sampling。
-
TD target 由两部分组成,一部分是 sampling,一部分是bootstrapping。
-
Unified View: Dynamic Programming Backup
DP 是直接算 expectation,把它所有相关的状态都进行加和。

-
Unified View: Monte-Carlo Backup
MC 在当前状态下,采一个支路,在一个path 上进行更新,更新这个 path 上的所有状态。

-
Unified View: Temporal-Difference Backup
TD 是从当前状态开始,往前走了一步,关注的是非常局部的步骤。
-
Unified View of Reinforcement Learning
3. Model-free Control
- Q: 当我们不知道 MDP 模型情况下,如何优化价值函数,得到最佳的策略?
- A: 我们可以把
policy iteration进行一个广义的推广,使它能够兼容 MC 和 TD 的方法,即Generalized Policy Iteration(GPI) with MC and TD。
3.1 Policy Iteration
-
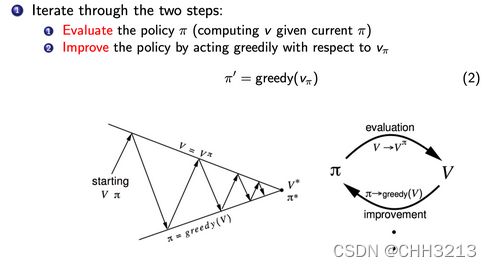
Policy iteration 由两个步骤组成:
3.1.1 Policy Iteration for a Known MDP

得到一个价值函数过后,我们并不知道它的奖励函数和状态转移,所以就没法估计它的 Q 函数。所以这里有一个问题:当我们不知道奖励函数和状态转移时,如何进行策略的优化。
3.1.2 Generalized Policy Iteration with Action-Value Function
- 针对上述情况,我们引入了广义的 policy iteration 的方法。
- 我们对 policy evaluation 部分进行修改:用 MC 的方法代替 DP 的方法去估计 Q 函数。
- 当得到 Q 函数后,就可以通过 greedy 的方法去改进它。
3.1.3 Monte Carlo with Exploring Starts
- 上图是用 MC 估计 Q 函数的算法。
- 假设每一个 episode 都有一个
exploring start,exploring start保证所有的状态和动作都在无限步的执行后能被采样到,这样才能很好地去估计。 - 算法通过 MC 的方法产生了很多的轨迹,每个轨迹都可以算出它的价值。然后,我们可以通过 average 的方法去估计 Q 函数。Q 函数可以看成一个 Q-table,通过采样的方法把表格的每个单元的值都填上,然后我们使用 policy improvement 来选取更好的策略。
- 假设每一个 episode 都有一个
- 算法核心:如何用 MC 方法来填 Q-table。
3.1.4 Monte Carlo with ε \varepsilon ε-Greedy Exploration
-
为了确保 MC 方法能够有足够的探索,我们使用了 ε \varepsilon ε-greedy exploration。
ε -greedy \varepsilon\text{-greedy} ε-greedy 的意思是说,我们有 1 − ε 1-\varepsilon 1−ε 的概率会按照Q-function 来决定 action,通常 ε \varepsilon ε就设一个很小的值, 1 − ε 1-\varepsilon 1−ε 可能是 90%,也就是 90% 的概率会按照 Q-function 来决定 action,但是你有 10% 的机率是随机的。通常在实现上 ε \varepsilon ε会随着时间递减。在最开始的时候。因为还不知道那个 action 是比较好的,所以你会花比较大的力气在做exploration。接下来随着训练的次数越来越多。已经比较确定说哪一个 Q 是比较好的。你就会减少你的 exploration,你会把 ε \varepsilon ε 的值变小,主要根据 Q-function 来决定你的 action,比较少做 random,这是 ε -greedy \varepsilon\text{-greedy} ε-greedy。
-
当我们使用 MC 和 ε \varepsilon ε-greedy 探索这个形式的时候,可以确保价值函数是单调的,改进的。

-
下图是带 ε \varepsilon ε-greedy 探索的 MC 算法的伪代码。
-
与 MC 相比,TD 有如下几个优势:
- 低方差。
- 能够在线学习。
- 能够从不完整的序列学习。
-
所以我们可以把 TD 也放到 control loop 里面去估计 Q-table,再采取 ε \varepsilon ε-greedy policy improvement。这样就可以在 episode 没结束的时候来更新已经采集到的状态价值。

3.1.5 On Policy First Visit Monte Carlo algorithm
3.1.6 Off Policy Monte Carlo Algorithm
3.2 Sarsa: On-policy TD Control
-
TD 给定了一个策略,然后我们去估计它的价值函数。接着我们要考虑怎么用 TD 这个框架来估计 Q-function。
-
Sarsa 所作出的改变很简单,就是将原本 TD 更新 V 的过程,变成了更新 Q,如下式所示:
Q Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left[R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right)-Q\left(S_{t}, A_{t}\right)\right] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]
这个公式表示可以拿下一步的 Q 值 Q ( S t + 1 , A t + 1 ) Q(S_{t+_1},A_{t+1}) Q(St+1,At+1) 来更新这一步的 Q 值 Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 。
3.2.1 sarsa 介绍
-
为了理解这个公式,如上图所示,我们先把 R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right.) Rt+1+γQ(St+1,At+1) 当作是一个目标值,就是 Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 想要去逼近的一个目标值。 R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right.) Rt+1+γQ(St+1,At+1)就是 TD target。
-
我们想要计算的就是 Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 。因为最开始 Q 值都是随机初始化或者是初始化为零,它需要不断地去逼近它理想中真实的 Q 值(TD target), R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right)-Q\left(S_{t}, A_{t}\right) Rt+1+γQ(St+1,At+1)−Q(St,At) 就是 TD 误差。
-
也就是说,我们拿 Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 来逼近 G t G_t Gt,那 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1,At+1) 其实就是近似 G t + 1 G_{t+1} Gt+1。我就可以用 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1,At+1) 近似 G t + 1 G_{t+1} Gt+1,然后把 ) R t + 1 + Q ( S t + 1 , A t + 1 ) )R_{t+1}+Q(S_{t+1},A_{t+1}) )Rt+1+Q(St+1,At+1)当成目标值。
-
Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 就是要逼近这个目标值,用软更新的方式来逼近。软更新的方式就是每次只更新点, α \alpha α 类似于学习率。最终的话,Q 值都是可以慢慢地逼近到真实的 target 值。这样更新公式只需要用到当前时刻的 S t S_{t} St,还有拿到的 R t + 1 , S t + 1 , A t + 1 R_{t+1}, S_{t+1},A_{t+1} Rt+1,St+1,At+1。
-
该算法由于每次更新值函数需要知道当前的状态(state)、当前的动作(action)、奖励(reward)、下一步的状态(state)、下一步的动作(action),即 ) ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) )(S_{t}, A_{t}, R_{t+1}, S_{t+1}, A_{t+1}) )(St,At,Rt+1,St+1,At+1)这几个值 ,由此得名 Sarsa 算法。它走了一步之后,拿到了 ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) (S_{t}, A_{t}, R_{t+1}, S_{t+1}, A_{t+1}) (St,At,Rt+1,St+1,At+1)之后,就可以做一次更新。
3.2.2 n-step Sarsa
- Sarsa 属于单步更新法,也就是说每执行一个动作,就会更新一次价值和策略。如果不进行单步更新,而是采取 n n n 步更新或者回合更新,即在执行 n n n 步之后再来更新价值和策略,这样就得到了 n 步 Sarsa(n-step Sarsa)。

具体来说,对于 Sarsa,在 t t t 时刻其价值的计算公式为
q t = R t + 1 + γ Q ( S t + 1 , A t + 1 ) q_{t}=R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right) qt=Rt+1+γQ(St+1,At+1)
而对于 n n n 步 Sarsa,它的 n n n 步 Q 计算为
q t ( n ) = R t + 1 + γ R t + 2 + … + γ n − 1 R t + n + γ n Q ( S t + n , A t + n ) q_{t}^{(n)}=R_{t+1}+\gamma R_{t+2}+\ldots+\gamma^{n-1} R_{t+n}+\gamma^{n} Q\left(S_{t+n}, A_{t+n}\right) qt(n)=Rt+1+γRt+2+…+γn−1Rt+n+γnQ(St+n,At+n)
如果给 q t ( n ) q_t^{(n)} qt(n) 加上衰减因子 λ \lambda λ 并进行求和,即可得到 Sarsa( λ \lambda λ) 的 Q :
q t λ = ( 1 − λ ) ∑ n = 1 ∞ λ n − 1 q t ( n ) q_{t}^{\lambda}=(1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} q_{t}^{(n)} qtλ=(1−λ)n=1∑∞λn−1qt(n)
因此, n n n 步 Sarsa( λ \lambda λ)的更新策略可以表示为
Q ( S t , A t ) ← Q ( S t , A t ) + α ( q t λ − Q ( S t , A t ) ) Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left(q_{t}^{\lambda}-Q\left(S_{t}, A_{t}\right)\right) Q(St,At)←Q(St,At)+α(qtλ−Q(St,At))
总的来说,Sarsa 和 Sarsa( λ \lambda λ) 的差别主要体现在价值的更新上。
-
了解单步更新的一个基本公式之后,代码实现就很简单了。右边是环境,左边是 agent 。我们每次跟环境交互一次之后呢,就可以 learn 一下,向环境输出 action,然后从环境当中拿到 state 和 reward。Agent 主要实现两个方法:
3.2.3 算法伪代码
3.3 Q-learning: Off-policy TD Control
3.3.1 off-policy 介绍
-
Sarsa 是一种 on-policy 策略。Sarsa 优化的是它实际执行的策略,它直接拿下一步会执行的 action 来去优化 Q 表格,所以 on-policy 在学习的过程中,只存在一种策略,它用一种策略去做 action 的选取,也用一种策略去做优化。所以 Sarsa 知道它下一步的动作有可能会跑到悬崖那边去,所以它就会在优化它自己的策略的时候,会尽可能的离悬崖远一点。这样就可以保证,它下一步哪怕是有随机动作,它也还是在安全区域内。
-
而 off-policy 在学习的过程中,有两种不同的策略:
- 第一个策略是我们需要去学习的策略,即target policy(目标策略),一般用 π \pi π 来表示,Target policy 就像是在后方指挥战术的一个军师,它可以根据自己的经验来学习最优的策略,不需要去和环境交互。
- 另外一个策略是探索环境的策略,即behavior policy(行为策略),一般用 μ \mu μ 来表示。 μ \mu μ 可以大胆地去探索到所有可能的轨迹,采集轨迹,采集数据,然后把采集到的数据喂给 target policy 去学习。而且喂给目标策略的数据中并不需要 A t + 1 A_{t+1} At+1 ,而 Sarsa 是要有 A t + 1 A_{t+1} At+1 的。Behavior policy 像是一个战士,可以在环境里面探索所有的动作、轨迹和经验,然后把这些经验交给目标策略去学习。比如目标策略优化的时候,Q-learning 不会管你下一步去往哪里探索,它就只选收益最大的策略。
-
在 off-policy learning 的过程中,轨迹都是 behavior policy 跟环境交互产生的,产生这些轨迹后,我们使用这些轨迹来更新 target policy π \pi π。
-
Off-policy learning 有很多好处:
- 我们可以利用 behavior policy 来学到一个最佳的策略,学习效率高;
- 可以让我们学习其他 agent 的行为,模仿学习,学习人或者其他 agent 产生的轨迹;
- 重用旧的策略产生的轨迹。探索过程需要很多计算资源,这样的话,可以节省资源。
3.3.2 Q-learning
-
Q-learning 有两种 policy:behavior policy 和 target policy。
-
Target policy π \pi π 直接在 Q-table 上取 greedy,就取它下一步能得到的所有状态,如下式所示:
π ( S t + 1 ) = arg max a ′ Q ( S t + 1 , a ′ ) \pi\left(S_{t+1}\right)=\underset{a^{\prime}}{\arg \max}~ Q\left(S_{t+1}, a^{\prime}\right) π(St+1)=a′argmax Q(St+1,a′) -
Behavior policy μ \mu μ 可以是一个随机的 policy,但我们采取 ε -greedy \varepsilon\text{-greedy} ε-greedy,让 behavior policy 不至于是完全随机的,它是基于 Q-table 逐渐改进的。
-
我们可以构造 Q-learning target,Q-learning 的 next action 都是通过 arg max 操作来选出来的,于是我们可以代入 arg max 操作,可以得到下式:
R t + 1 + γ Q ( S t + 1 , A ′ ) = R t + 1 + γ Q ( S t + 1 , arg max Q ( S t + 1 , a ′ ) ) = R t + 1 + γ max a ′ Q ( S t + 1 , a ′ ) \begin{aligned} R_{t+1}+\gamma Q\left(S_{t+1}, A^{\prime}\right) &=R_{t+1}+\gamma Q\left(S_{t+1},\arg \max ~Q\left(S_{t+1}, a^{\prime}\right)\right) \\ &=R_{t+1}+\gamma \max _{a^{\prime}} Q\left(S_{t+1}, a^{\prime}\right) \end{aligned} Rt+1+γQ(St+1,A′)=Rt+1+γQ(St+1,argmax Q(St+1,a′))=Rt+1+γa′maxQ(St+1,a′) -
接着我们可以把 Q-learning 更新写成增量学习的形式,TD target 就变成 max 的值,即
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left[R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a\right)-Q\left(S_{t}, A_{t}\right)\right] Q(St,At)←Q(St,At)+α[Rt+1+γamaxQ(St+1,a)−Q(St,At)]
3.3.3 算法伪代码
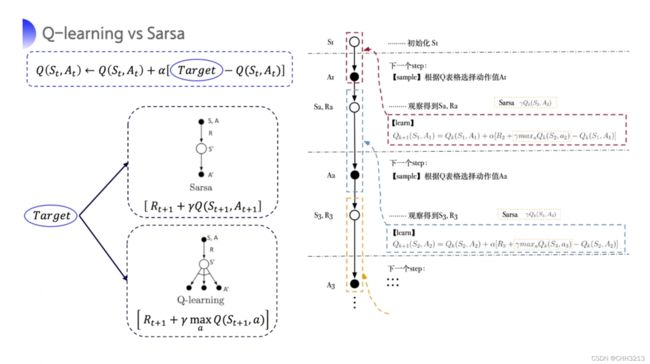
3.3.4 Q learning VS Sarsa
- Q-learning 是 off-policy 的时序差分学习方法,Sarsa 是 on-policy 的时序差分学习方法。
- Sarsa 在更新 Q 表格的时候,它用到 A’ 。要获取下一个 Q 值的时候,A’ 是下一个 step 一定会执行的 action。这个 action 有可能是 ε \varepsilon ε-greedy 方法采样出来的值,也有可能是 max Q 对应的 action,也有可能是随机动作,但这是它实际执行的那个动作。
- Q-learning 在更新 Q 表格的时候,它用到这个的 Q 值 Q ( S ′ , a ) Q(S',a) Q(S′,a) 对应的那个 action ,它不一定是下一个 step 会执行的实际的 action,因为你下一个实际会执行的那个 action 可能会探索。
- Q-learning 默认的 next action 不是通过 behavior policy 来选取的,Q-learning 直接看 Q-table,取它的 max 值,它默认 A’ 为最优策略选的动作,所以 Q-learning 在学习的时候,不需要传入 A’,即 A t + 1 A_{t+1} At+1 的值。
-
Sarsa 和 Q-learning 的更新公式都是一样的,区别只在 target 计算的这一部分
- Sarsa 是 R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1}+\gamma Q(S_{t+1}, A_{t+1}) Rt+1+γQ(St+1,At+1) ;
- Q-learning 是 R t + 1 + γ max a Q ( S t + 1 , a ) R_{t+1}+\gamma \underset{a}{\max} Q\left(S_{t+1}, a\right) Rt+1+γamaxQ(St+1,a)。
-
Sarsa 是用自己的策略产生了 S,A,R,S’,A’ 这一条轨迹。然后拿着 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1,At+1)去更新原本的 Q 值 Q ( S t , A t ) Q(S_t,A_t) Q(St,At)。
-
Q-learning 并不需要知道实际上选择哪一个 action ,它默认下一个动作就是 Q 最大的那个动作。Q-learning 知道实际上 behavior policy 可能会有 10% 的概率去选择别的动作,但 Q-learning 并不担心受到探索的影响,它默认了就按照最优的策略来去优化目标策略,所以它可以更大胆地去寻找最优的路径,它会表现得比 Sarsa 大胆非常多。
-
对 Q-learning 进行逐步地拆解的话,跟 Sarsa 唯一一点不一样就是并不需要提前知道 A 2 A_2 A2 ,就能更新 Q ( S 1 , A 1 ) Q(S_1,A_1) Q(S1,A1) 。在训练一个 episode 这个流程图当中,Q-learning 在 learn 之前它也不需要去拿到 next action A ′ A' A′,它只需要前面四个 $ (S,A,R,S’)$,这跟 Sarsa 很不一样。
4. On-policy vs. Off-policy
- Sarsa 是一个典型的 on-policy 策略,它只用了一个 policy π \pi π,它不仅使用策略 π \pi π 学习,还使用策略 π \pi π 与环境交互产生经验。如果 policy 采用 ε \varepsilon ε-greedy 算法的话,它需要兼顾探索,为了兼顾探索和利用,它训练的时候会显得有点胆小。它在解决悬崖问题的时候,会尽可能地离悬崖边上远远的,确保说哪怕自己不小心探索了一点,也还是在安全区域内。此外,因为采用的是 ε \varepsilon ε-greedy 算法,策略会不断改变( ε \varepsilon ε 会不断变小),所以策略不稳定。
- Q-learning 是一个典型的 off-policy 的策略,它有两种策略:target policy 和 behavior policy。它分离了目标策略跟行为策略。Q-learning 就可以大胆地用 behavior policy 去探索得到的经验轨迹来去优化目标策略,从而更有可能去探索到最优的策略。Behavior policy 可以采用 ε \varepsilon ε-greedy 算法,但 target policy 采用的是 greedy 算法,直接根据 behavior policy 采集到的数据来采用最优策略,所以 Q-learning 不需要兼顾探索。
- 比较 Q-learning 和 Sarsa 的更新公式可以发现,Sarsa 并没有选取最大值的 max 操作,因此,
- Q-learning 是一个非常激进的算法,希望每一步都获得最大的利益;
- 而 Sarsa 则相对非常保守,会选择一条相对安全的迭代路线。
5. 练习
5.1 简答题
5.1.1 Q表格型表示方法
表示形式是一种表格形式,其中横坐标为 action(agent)的行为,纵坐标是环境的state,其对应着每一个时刻agent和环境的情况,并通过对应的reward反馈去做选择。一般情况下,Q表格是一个已经训练好的表格,不过,我们也可以每进行一步,就更新一下Q表格,然后用下一个状态的Q值来更新这个状态的Q值(即时序差分方法)。
5.1.2 时序差分(Temporal Difference)
一种Q函数(Q值)的更新方式,也就是可以拿下一步的 Q 值 Q ( S t + 1 , A t + 1 ) Q(S_{t+_1},A_{t+1}) Q(St+1,At+1)来更新我这一步的 Q 值 Q ( S t , A t ) Q(S_t,A_t) Q(St,At) 。完整的计算公式如下:
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t,A_t) \larr Q(S_t,A_t) + \alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]
5.2 问答题
5.2.1 基于SARSA算法的agent的学习过程?
答:我们现在有环境,有agent。每交互一次以后,我们的agent会向环境输出action,接着环境会反馈给agent当前时刻的state和reward。那么agent此时会实现两个方法:
-
使用已经训练好的Q表格,对应环境反馈的state和reward选取对应的action进行输出。
-
我们已经拥有了 ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) (S_{t}, A_{t}, R_{t+1}, S_{t+1}, A_{t+1}) (St,At,Rt+1,St+1,At+1) 这几个值,并直接使用 A t + 1 A_{t+1} At+1 去更新我们的Q表格。
5.2.2 能否简述on-policy和off-policy的区别?
答:
- off-policy和on-policy的根本区别在于生成样本的policy和参数更新时的policy是否相同。
- 对于on-policy,行为策略和要优化的策略是一个策略,更新了策略后,就用该策略的最新版本对于数据进行采样;
- 对于off-policy,使用任意的一个行为策略来对于数据进行采样,并利用其更新目标策略。
- 如果举例来说,Q-learning在计算下一状态的预期收益时使用了max操作,直接选择最优动作,而当前policy并不一定能选择到最优的action,因此这里生成样本的policy和学习时的policy不同,所以Q-learning为off-policy算法;
- 相对应的SARAS则是基于当前的policy直接执行一次动作选择,然后用这个样本更新当前的policy,因此生成样本的policy和学习时的policy相同,所以SARAS算法为on-policy算法。
理想情况下,强化学习应该直奔最优策略而去–确定性的“状态-最优行为选择”。我们称之为target policy。
这是on-policy的目标,但在实施时,会遭遇探索-利用的矛盾:光利用目前已知的最优选择,可能学不到最优解,收敛到局部最优;而加入探索又降低了学习效率。epsilon-greedy 算法是这种矛盾下的折衷。
为避免on policy的问题,off policy索性把问题一分为二,采取了从行为策略来学习目标策略的办法,两者可以互不干扰。具体来说:先产生某概率分布下的大量行为数据(behavior policy),意在探索。从这些偏离(off)最优策略的数据中寻求target policy。当然这么做是需要满足数学条件的:假設π是目标策略, µ是行为策略,那么从µ学到π的条件是:π(a|s) > 0 必然有 µ(a|s) > 0成立。
优缺点:
on-policy优点是直接了当,速度快,劣势是不一定找到最优策略。
off-policy劣势是曲折,收敛慢,但优势是更为强大和通用。其强大是因为它确保了数据全面性,所有行为都能覆盖。甚至其数据来源可以多样,自行产生、或者外来数据均可。
这两种方法无绝对优劣之分,看不同的环境来选择最优办法。
5.2.3 能否讲一下Q-Learning?
答:
- Q-learning是通过计算最优动作值函数来求策略的一种时序差分的学习方法,其更新公式为:
Q ( s , a ) ← Q ( s , a ) + α [ r ( s , a ) + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s, a) \larr Q(s, a) + \alpha [r(s,a) + \gamma \max_{a'} Q(s', a') - Q(s, a)] Q(s,a)←Q(s,a)+α[r(s,a)+γa′maxQ(s′,a′)−Q(s,a)]
是off-policy的,由于Q更新使用了下一个时刻的最大值,所以我们只关心哪个动作使得 Q ( s t + 1 , a ) Q(s_{t+1}, a) Q(st+1,a) 取得最大值,而实际到底采取了哪个动作(行为策略),并不关心。这表明优化策略并没有用到行为策略的数据,所以说它是 off-policy 的。
5.2.4 能否讲一下SARSA?
答:
SARSA可以算是Q-learning的改进(这句话出自「神经网络与深度学习」的第 342 页)(可参考SARSA「on-line q-learning using connectionist systems」的 abstract 部分),其更新公式为:
Q ( s , a ) ← Q ( s , a ) + α [ r ( s , a ) + γ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s, a) \larr Q(s, a) + \alpha [r(s,a) + \gamma Q(s', a') - Q(s, a)] Q(s,a)←Q(s,a)+α[r(s,a)+γQ(s′,a′)−Q(s,a)]
SARSA必须执行两次动作得到 ( s , a , r , s ′ , a ′ ) (s,a,r,s',a') (s,a,r,s′,a′)才可以更新一次;而且 a ′ a' a′是在特定策略 π \pi π 的指导下执行的动作,因此估计出来的 Q ( s , a ) Q(s,a) Q(s,a) 是在该策略 π \pi π 之下的Q-value,样本生成用的 π \pi π和估计的 π \pi π 是同一个,因此是on-policy。
5.2.5 请问value-based和policy-based的区别是什么?
答:
- 生成policy上的差异:前者确定,后者随机。Value-Base中的 action-value估计值最终会收敛到对应的true values(通常是不同的有限数,可以转化为0到1之间的概率),因此通常会获得一个确定的策略(deterministic policy);而Policy-Based不会收敛到一个确定性的值,另外他们会趋向于生成optimal stochastic policy。如果optimal policy是deterministic的,那么optimal action对应的性能函数将远大于suboptimal actions对应的性能函数,性能函数的大小代表了概率的大小。
- 动作空间是否连续,前者离散,后者连续。Value-Base,对于连续动作空间问题,虽然可以将动作空间离散化处理,但离散间距的选取不易确定。过大的离散间距会导致算法取不到最优action,会在这附近徘徊,过小的离散间距会使得action的维度增大,会和高维度动作空间一样导致维度灾难,影响算法的速度;而Policy-Based适用于连续的动作空间,在连续的动作空间中,可以不用计算每个动作的概率,而是通过Gaussian distribution (正态分布)选择action。
- value-based,例如Q-learning,是通过求解最优值函数间接的求解最优策略;policy-based,例如REINFORCE,Monte-Carlo Policy Gradient,等方法直接将策略参数化,通过策略搜索,策略梯度或者进化方法来更新策略的参数以最大化回报。基于值函数的方法不易扩展到连续动作空间,并且当同时采用非线性近似、自举和离策略时会有收敛性问题。策略梯度具有良好的收敛性证明。
- 策略迭代。它有两个循环,一个是在策略估计的时候,为了求当前策略的值函数需要迭代很多次。另外一个是外面的大循环,就是策略评估,策略提升这个循环。值迭代算法则是一步到位,直接估计最优值函数,因此没有策略提升环节。
5.2.6 请简述以下时序差分(Temporal Difference,TD)算法。
答:
TD算法是使用广义策略迭代来更新Q函数的方法,核心使用了自举(bootstrapping),即值函数的更新使用了下一个状态的值函数来估计当前状态的值。也就是使用下一步的 Q Q Q 值 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1,At+1) 来更新我这一步的 Q 值 Q ( S t , A t ) Q(S_t,A_t) Q(St,At)。完整的计算公式如下:
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) ] Q(S_t,A_t) \larr Q(S_t,A_t) + \alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)]
5.2.7 请问蒙特卡洛方法(Monte Carlo Algorithm,MC)和时序差分(Temporal Difference,TD)算法是无偏估计吗?
答:蒙特卡洛方法(MC)是无偏估计,时序差分(TD)是有偏估计;MC的方差较大,TD的方差较小,原因在于TD中使用了自举(bootstrapping)的方法,实现了基于平滑的效果,导致估计的值函数的方差更小。
5.2.8 能否简单说下动态规划、蒙特卡洛和时序差分的异同点?
答:
-
相同点:都用于进行值函数的描述与更新,并且所有方法都是基于对未来事件的展望来计算一个回溯值。
-
不同点:蒙特卡洛和TD算法隶属于model-free,而动态规划属于model-based;TD算法和蒙特卡洛的方法,因为都是基于model-free的方法,因而对于后续状态的获知也都是基于试验的方法;TD算法和动态规划的策略评估,都能基于当前状态的下一步预测情况来得到对于当前状态的值函数的更新。
-
另外,TD算法不需要等到实验结束后才能进行当前状态的值函数的计算与更新,而蒙特卡洛的方法需要试验交互,产生一整条的马尔科夫链并直到最终状态才能进行更新。TD算法和动态规划的策略评估不同之处为model-free和model-based 这一点,动态规划可以凭借已知转移概率就能推断出来后续的状态情况,而TD只能借助试验才能知道。
-
蒙特卡洛方法和TD方法的不同在于,蒙特卡洛方法进行完整的采样来获取了长期的回报值,因而在价值估计上会有着更小的偏差,但是也正因为收集了完整的信息,所以价值的方差会更大,原因在于毕竟基于试验的采样得到,和真实的分布还是有差距,不充足的交互导致的较大方差。而TD算法与其相反,因为只考虑了前一步的回报值 其他都是基于之前的估计值,因而相对来说,其估计值具有偏差大方差小的特点。
-
三者的联系:对于 T D ( λ ) TD(\lambda) TD(λ)方法,如果 λ = 0 \lambda = 0 λ=0 ,那么此时等价于TD,即只考虑下一个状态;如果 λ = 1 \lambda = 1 λ=1,等价于MC,即考虑 T − 1 T-1 T−1个后续状态即到整个episode序列结束。
6. 编程题
6.1 使用Q-learning解决悬崖寻路问题
项目采用gym开发的CliffWalking-v0环境,在上面实现一个简单的Q-learning入门demo。
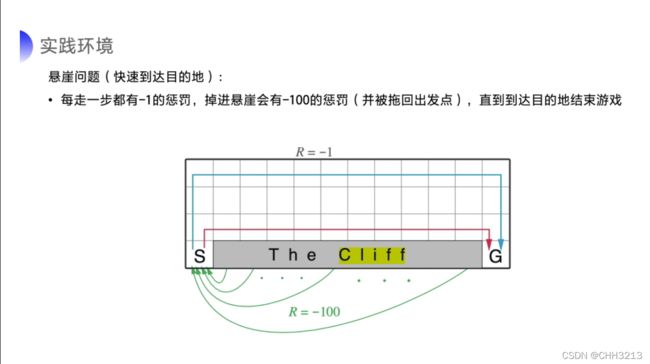
6.1.1 CliffWalking-v0环境简介
首先对该环境做一个简介,该环境中文名称叫悬崖寻路问题(CliffWalking),是指在一个4 x 12的网格中,智能体以网格的左下角位置为起点,以网格的下角位置为终点,目标是移动智能体到达终点位置,智能体每次可以在上、下、左、右这4个方向中移动一步,每移动一步会得到-1单位的奖励。
如图,红色部分表示悬崖,数字代表智能体能够观测到的位置信息,即observation,总共会有0-47等48个不同的值,智能体在移动中会有以下限制:
智能体不能移出网格,如果智能体想执行某个动作移出网格,那么这一步智能体不会移动,但是这个操作依然会得到-1单位的奖励
如果智能体“掉入悬崖” ,会立即回到起点位置,并得到-100单位的奖励
当智能体移动到终点时,该回合结束,该回合总奖励为各步奖励之和
6.1.2 算法实现
算法实现代码见于github仓库。
-
注意 ε \varepsilon ε-greedy 策略的使用,以及相应的参数 ε \varepsilon ε如何衰减
-
训练模型和测试模型的时候选择动作有一些不同,训练时采取 ε \varepsilon ε-greedy策略,而测试时直接选取Q值最大对应的动作,所以算法在动作选择的时候会包括choose_action(训练时的动作采样)和predict(测试时的动作选择)
-
Q值最大对应的动作可能不止一个,此时可以随机选择一个输出结果
6.2 使用Sarsa解决悬崖寻路问题
与q learning算法基本一致,只有q表格更新部分不同,算法实现代码见于github仓库。
6.3 使用蒙特卡洛算法解决悬崖寻路问题
代码实现见于github仓库