数据结构期末复习（1）数据结构和算法 线性表

数据结构期末总复习（gaois课堂版）

数据结构的概念

数据结构是计算机科学中的一个重要概念，它指的是组织和存储数据的方式。数据结构可以帮助我们高效地操作和管理数据，使得计算机程序能够更加有效地执行各种任务。

数据结构有很多种类，常见的包括数组、链表、栈、队列、树、图等。每种数据结构都有其特定的特点和适用场景。

数组是一种线性数据结构，它由一系列相同类型的元素组成，通过索引来访问元素。数组的主要优点是可以快速随机访问元素，但插入和删除元素的操作相对较慢。

链表也是一种线性数据结构，它由一系列节点组成，每个节点包含自身的数据和指向下一个节点的指针。链表的优点是插入和删除元素的操作比较快，但访问特定位置的元素需要遍历整个链表。

栈是一种后进先出（LIFO）的数据结构，只允许在栈顶进行插入和删除操作。栈常用于实现函数调用、表达式求值等场景。

队列是一种先进先出（FIFO）的数据结构，只允许在队尾插入元素，在队头删除元素。队列常用于实现任务调度、缓冲区等场景。

树是一种非线性数据结构，由节点和边组成。每个节点可以有多个子节点，从根节点开始遍历整个树。树常用于实现搜索、排序、存储层次关系等场景。常见的树结构包括二叉树、二叉搜索树、平衡树等。

图是一种由节点和边组成的非线性数据结构，节点之间的连接关系可以是任意的。图常用于表示网络、社交关系、路径搜索等场景。

选择合适的数据结构对于解决具体问题非常重要，不同的数据结构具有不同的性能特点和适用场景，需要根据具体的需求进行选择和应用。

在数据结构中，(D, S) 表示一个数据结构 D 和相应的操作集合 S。通常情况下，D 是指数据结构的定义和存储方式，而 S 则包括了可以对该数据结构进行的各种操作。

举例来说，对于栈这种数据结构，可以表示为 (Stack, {push, pop, isEmpty, peek})，其中 Stack 是栈的定义，{push, pop, isEmpty, peek} 是可以对栈执行的操作集合。

• push：将元素压入栈顶。
• pop：从栈顶弹出元素。
• isEmpty：判断栈是否为空。
• peek：查看栈顶元素但不移除。

通过定义数据结构和操作集合，我们可以清楚地描述出数据结构的特性和可用的操作，更方便地进行程序设计和实现。不同的数据结构可能有不同的操作集合，适用于不同的场景和问题解决方式。

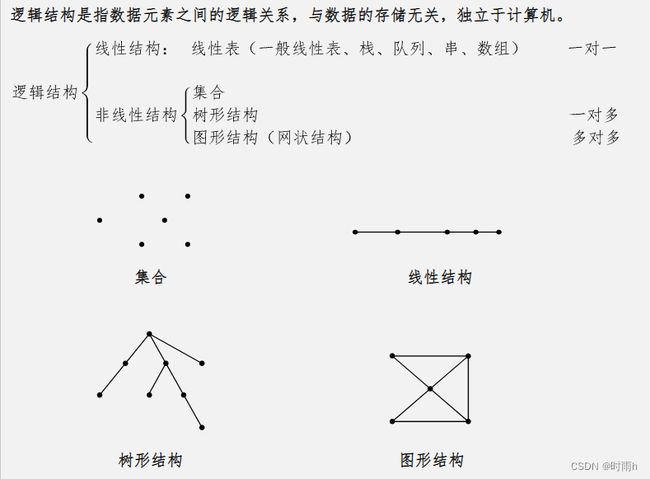
1. 线性结构：数据元素之间存在一对一的关系，线性结构可以分为线性表、栈和队列等。线性表中的数据元素排成一条直线，栈和队列则是线性表的特殊形式。

2. 非线性结构：数据元素之间存在一对多或多对多的关系，非线性结构可以分为树和图等。树结构中的数据元素呈现出层次关系，图结构中的数据元素之间可以是任意关系。

3. 集合结构：数据元素之间没有特定的关系，集合结构中的元素是无序的，每个元素都是独立的。

逻辑结构主要用于描述数据元素之间的关系和组织方式，而与具体的存储方式无关。根据实际需求，我们可以选择不同的逻辑结构来组织和处理数据，以便更好地满足问题的要求。

常见的数据结构存储结构有以下几种：

1. 顺序存储结构：也称为数组存储结构，是将元素按照一定的顺序依次存放在一段连续的内存空间中。通过下标可以直接访问元素，具有随机访问的特点。但是插入和删除操作需要移动大量元素，效率较低。

2. 链式存储结构：是将元素存储在不连续的内存空间中，并通过指针连接起来。插入和删除操作仅需要修改指针，效率较高，但是访问元素需要遍历整个链表，效率较低。

3. 树形存储结构：是一种层次结构，每个节点有零个或多个子节点。通常有二叉树、B树、B+树等。二叉树最常用的存储方式是链式存储，B树和B+树则采用了顺序存储和链式存储的结合方式。

4. 散列表：也称为哈希表，是一种根据关键字直接进行访问的数据结构。它通过关键字的哈希值映射到对应的位置上，查找、插入和删除的时间复杂度都为 O(1)。

5. 图形存储结构：是一种由节点和边组成的非线性结构，通常有邻接矩阵和邻接表两种存储方式。邻接矩阵用一个二维数组来表示节点之间的连接关系，邻接表则是用链表的形式表示。

6. 索引存储是一种常用的数据存储结构，它通过使用索引来提高数据的检索效率。索引是一种数据结构，它包含了关键字和对应数据位置的映射关系，可以快速定位到所需数据的位置。

在索引存储结构中，通常存在两种主要的索引类型：

1. 主索引：主索引是基于数据表的主键或唯一键构建的索引。主索引中的关键字与数据记录一一对应，通过主索引可以直接访问到具体的数据记录，因此具有很高的检索效率。

2. 辅助索引：辅助索引是基于非主键的其他列构建的索引。辅助索引中的关键字并不与数据记录一一对应，而是指向对应数据记录的物理地址或指针。通过辅助索引可以快速定位到满足特定条件的数据记录，但需要通过进一步的查找才能获得完整的数据。

索引存储结构的优点是可以大大提高数据的检索效率，减少了查找整个数据集的时间复杂度。同时，索引还可以提供排序功能和加速数据的插入、更新和删除操作。但索引也需要占用额外的存储空间，并且在数据的插入、更新和删除时需要维护索引结构，会增加一定的开销。

在实际应用中，根据具体的数据特点和查询需求，我们需要合理地选择和设计索引存储结构，以提高系统的性能和响应速度。

不同的存储结构适用于不同的场景和问题解决方式。我们需要在实际应用中，根据需求选择最合适的存储结构，以便更好地满足问题的要求。

算法

算法是一组解决特定问题的有限步骤。它是一种精确的、明确的、自动的计算过程，通过输入数据并处理它们来产生输出结果。算法是计算机科学中最基本的概念之一，也是计算机程序的核心部分。

算法具有以下几个重要的特点：

1. 精确性：算法必须是精确的，即每个步骤都必须明确、无歧义地定义。

2. 有限性：算法必须能在有限的时间和空间内完成计算。

3. 可行性：算法必须是可行的，即能够在计算机等计算设备上执行。

4. 输入输出：算法必须有输入和输出，即将输入转换为输出的过程。

5. 通用性：算法必须是通用的，即能够解决一类问题而不是特定的单个问题。

6. 可读性：算法必须是可读的，即容易理解和实现，并且易于维护和修改。

算法可以分为多种类型，常见的分类方式包括：

1. 按照解决问题的领域分类，如图像处理、网络优化、数据挖掘等。

2. 按照算法设计思想分类，如贪心算法、分治算法、动态规划算法、回溯算法等。

3. 按照算法的性质分类，如排序算法、查找算法、字符串匹配算法等。

在实际应用中，我们需要根据具体问题的特点和需求选择合适的算法以提高计算效率，并且对算法进行优化以满足不同的性能要求。

算法效率通常可以通过时间复杂度和空间复杂度来度量

时间复杂度指的是算法执行所需要的时间，通常使用大O符号来表示。例如，一个算法的时间复杂度为O(n)，表示随着输入规模n的增加，算法执行所需要的时间以线性方式增长。

空间复杂度指的是算法执行所需要的内存空间，同样也使用大O符号来表示。例如，一个算法的空间复杂度为O(n)，表示算法在执行期间最多需要占用n个单位的内存空间。

在实际应用中，我们需要根据具体问题的特点和要求，选择合适的算法以满足时间复杂度和空间复杂度的要求。通常情况下，时间复杂度和空间复杂度之间存在一定的权衡关系，有时需要进行折中取舍。例如，在一些对计算速度要求较高的场景中，我们可能更愿意牺牲一定的内存空间来提高执行效率；而在一些内存受限的场景中，我们可能更愿意使用空间复杂度较小的算法。

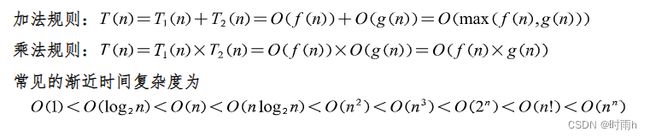
算法效率通常可以通过时间复杂度和空间复杂度来度量和评估。时间复杂度是指算法解决问题所需的时间量级，它描述了算法的运行时间随着输入规模增长时的增长率。常见的时间复杂度有常数时间 O(1)、线性时间 O(n)、对数时间 O(log n)、平方时间 O(n^2)等。

空间复杂度是指算法解决问题所需的存储空间量级，它描述了算法所需的额外空间随着输入规模增长时的增长率。常见的空间复杂度有常数空间 O(1)、线性空间 O(n)、对数空间 O(log n)等。

评估算法的时间复杂度和空间复杂度可以帮助我们比较不同算法之间的效率，选择最优的算法来解决问题。通常情况下，我们希望找到时间复杂度尽可能低且空间复杂度较小的算法，以提高程序的执行效率和节省资源的使用。

时间复杂度的频度计算

*是指对于算法中每个基本操作的执行次数进行统计和计算，从而得出算法的总执行次数。*具体地说，可以通过以下步骤来计算算法的时间复杂度：

1. 确定算法中需要执行的基本操作。基本操作通常包括算术运算、比较运算、赋值操作等。

2. 对于每个基本操作，估算它在算法中被执行的次数。这通常需要根据问题的规模和算法的实现方式进行分析和推导，并结合实际代码进行验证。

3. 将每个基本操作的执行次数相加，并用大 O 记号表示算法的时间复杂度。这里的大 O 记号表示算法的最坏情况时间复杂度，即在所有可能的输入情况下，算法的最长执行时间。

例如，对于以下求解数组元素和的算法：

int sum = 0;
for(int i=0; i<n; i++){
    sum += a[i];
}

其中，基本操作是一个加法操作 sum += a[i]，它在循环中被执行了 n 次。因此，算法的总执行次数为 n 次，时间复杂度为 O(n)。

再例如，对于以下查找有序数组中是否存在某个元素的二分查找算法：

int binarySearch(int[] a, int x){
    int low = 0, high = a.length - 1;
    while(low <= high){
        int mid = (low + high) / 2;
        if(a[mid] == x){
            return mid;
        }else if(a[mid] < x){
            low = mid + 1;
        }else{
            high = mid - 1;
        }
    }
    return -1;
}

其中，基本操作包括一个比较运算 a[mid] == x 和两个赋值操作 low = mid + 1 和 high = mid - 1。每次循环中至少执行一次比较运算和一个赋值操作，因此总执行次数为 log n（以 2 为底），时间复杂度为 O(log n)。

需要注意的是，算法的时间复杂度并不是具体的执行时间，而是对算法执行时间的一种抽象描述。它只考虑了算法在不同输入规模下的增长趋势，而没有考虑实际运行过程中的常数因子、系数和常数项等因素。因此，两个时间复杂度相同的算法在具体执行时间上可能存在较大差异，需要根据具体情况进行选择。

线性表

线性表的类型定义可以根据具体的编程语言来进行，以下是一些常见编程语言中线性表的类型定义示例：

在C语言中，可以使用结构体来定义线性表类型：

typedef struct {
    int data[MAX_SIZE];  // 存储线性表元素的数组
    int length;         // 线性表的当前长度
} LinearList;

在Java语言中，可以使用类来定义线性表类型：

public class LinearList {
    private int[] data;   // 存储线性表元素的数组
    private int length;   // 线性表的当前长度

    public LinearList(int maxSize) {
        data = new int[maxSize];
        length = 0;
    }
}

在Python语言中，可以使用类或者列表来定义线性表类型：

class LinearList:
    def __init__(self, max_size):
        self.data = [None] * max_size   # 存储线性表元素的列表
        self.length = 0

# 或者直接使用列表
linear_list = []

1. InitList(&L): 初始化表。这个操作用于构造一个空的线性表，即创建一个可以存储数据元素的容器。在具体实现时，可以根据编程语言的要求进行相应的初始化。

2. Length(L): 求表长。该操作用于返回线性表L中数据元素的个数，也就是表的长度。通过遍历线性表，计算元素个数即可得到表的长度。

3. LocateElem(L, e): 按值查找操作。该操作用于在线性表L中查找具有给定关键字值e的元素。它会返回第一个匹配到的元素的位置。需要遍历线性表，逐个比较元素的值与给定值e是否相等。

4. GetElem(L, i): 按位查找操作。该操作用于获取线性表L中第i个位置的元素的值。需要注意，线性表的索引通常从1开始。因此，该操作会返回第i个位置上的元素的值。

5. ListInsert(&L, i, e): 插入操作。该操作在线性表L的第i个位置上插入指定元素e。在插入之前，需要将第i个位置及其后面的所有元素后移一位，为新的元素腾出位置。

6. ListDelete(&L, i, &e): 删除操作。该操作用于删除线性表L中第i个位置的元素，并通过e返回被删除的元素的值。删除元素后，需要将第i个位置后面的所有元素前移一位，填补删除的空缺。

7. PrintList(L): 输出操作。该操作按照前后顺序输出线性表L的元素值。可以使用循环遍历线性表，并将每个元素的值依次输出。

8. Empty(L): 判空操作。该操作用于检查线性表L是否为空。如果线性表中没有任何元素，即为空表，则返回True；否则，返回False。

9. DestroyList(&L): 销毁操作。该操作用于销毁线性表L，释放相关的内存空间。在销毁之后，线性表将不再存在。

这些是线性表的基本操作，它们是实现线性表功能的基础。你可以根据需求选择并实现这些操作，以满足具体的编程需求。

顺序表的结构

顺序表是一种线性表的实现方式，它使用一段连续的存储空间来存储元素。在内存中，顺序表通常被表示为一个数组。下面是顺序表的结构：

typedef struct {
    ElementType *data;  // 指向存储元素的数组
    int length;         // 当前顺序表中的元素个数
    int capacity;       // 顺序表的容量，即数组的大小
} SeqList;

上面的结构体定义了一个顺序表的类型 SeqList。它包含了以下几个字段：

1. ElementType *data: 这是一个指针类型，指向存储元素的数组。每个数组元素可以存储一个数据元素，数据元素的类型由 ElementType 来定义，可以是任意类型。

2. int length: 这是一个整型变量，记录当前顺序表中的元素个数。初始时，length 为 0。

3. int capacity: 这是一个整型变量，表示顺序表的容量，即数组的大小。capacity 决定了顺序表能够容纳的最大元素个数。

顺序表的优点是可以快速根据位置访问元素，时间复杂度为O(1)。但是插入和删除操作可能需要移动大量元素，效率较低，时间复杂度为O(n)。

在具体编程实现中，还需要注意对顺序表容量的管理和动态扩容等问题。

顺序表随机查找

顺序表的主要特点之一就是支持随机存取，即通过元素的序号（或索引）可以在O(1)的时间复杂度内找到指定的元素。

这是因为顺序表的元素在存储时是按照一定的顺序依次排列在一块连续的内存空间中，每个元素占据一个固定大小的空间。因此，通过首地址和元素序号即可计算出指定元素在内存中的物理地址，从而实现随机存取。

与之相对比的是链表这种动态数据结构，它的元素在存储时并不是按照顺序存储在一块连续的内存空间中，而是通过指针链接起来的。因此，链表不支持随机存取，只能通过遍历整个链表来查找指定元素，时间复杂度为O(n)，其中n为链表的长度。

总的来说，顺序表的随机存取特性使得它在某些场景下具有优势，例如需要频繁访问指定位置的元素或进行排序等操作时，而链表则更适合于插入、删除等动态操作较多的场景。

线性表的动态分配

线性表的动态分配是指在线性表操作过程中，需要根据实际情况动态地分配内存空间来存储数据元素。动态分配可以避免事先预留过多的存储空间，节约内存资源。在线性表的动态分配中，通常使用指针来实现。

对于顺序表，动态分配的方式已经在之前回答中提到，这里再简单总结一下：

1. 初始时，可以通过 malloc 函数动态分配一定大小的存储空间，存储元素的数组称为 data。

2. 当存储空间不足以存放新元素时，需要通过 realloc 函数重新分配更大的存储空间，并将原来的数据复制到新的空间中。

3. 在释放存储空间前，需要使用 free 函数将分配的内存空间释放。

对于链表，动态分配的方式通常是通过节点的动态分配来实现。每个节点包含一个数据元素和一个指向下一个节点的指针。初始时，可以通过 malloc 函数动态分配一个节点的内存空间，并将数据元素和指针赋值给节点。当需要插入或删除节点时，只需要修改相应节点的指针即可。

需要注意的是，在动态分配内存空间时，需要管理分配的内存空间，防止出现内存泄漏等问题。在释放存储空间前，需要确保所有指向该空间的指针都已经被清空或修改，以避免访问已经释放的内存空间。

具体实现动态分配的线性表，我们可以以顺序表和链表为例进行说明。

1. 动态分配的顺序表实现：

#include 
#include 

typedef struct {
    int* data;  // 存储数据元素的数组
    int length; // 当前存储的元素个数
    int capacity; // 当前分配的存储空间容量
} SeqList;

void init(SeqList* list, int capacity) {
    list->data = (int*)malloc(sizeof(int) * capacity); // 初始分配存储空间
    list->length = 0;
    list->capacity = capacity;
}

void insert(SeqList* list, int element) {
    if (list->length >= list->capacity) {
        // 存储空间已满，需要扩容
        list->data = (int*)realloc(list->data, sizeof(int) * (list->capacity * 2));
        list->capacity *= 2;
    }
    list->data[list->length] = element; // 在末尾插入新元素
    list->length++;
}

void destroy(SeqList* list) {
    free(list->data); // 释放动态分配的存储空间
    list->data = NULL;
    list->length = 0;
    list->capacity = 0;
}

int main() {
    SeqList list;
    init(&list, 5); // 初始容量为5

    insert(&list, 1);
    insert(&list, 2);
    insert(&list, 3);
    insert(&list, 4);
    insert(&list, 5);
    insert(&list, 6); // 超过容量，进行扩容

    for (int i = 0; i < list.length; i++) {
        printf("%d ", list.data[i]); // 输出顺序表中的元素
    }
    printf("\n");

    destroy(&list);

    return 0;
}

2. 动态分配的链表实现：

#include 
#include 

typedef struct Node {
    int data;           // 数据元素
    struct Node* next;  // 指向下一个节点的指针
} Node;

typedef struct {
    Node* head; // 头节点
} LinkedList;

void init(LinkedList* list) {
    list->head = NULL; // 初始化为空链表
}

void insert(LinkedList* list, int element) {
    Node* newNode = (Node*)malloc(sizeof(Node)); // 动态分配新节点的内存空间
    newNode->data = element;
    newNode->next = NULL;

    if (list->head == NULL) {
        list->head = newNode; // 空链表，新节点成为头节点
    } else {
        Node* current = list->head;
        while (current->next != NULL) {
            current = current->next; // 找到链表的最后一个节点
        }
        current->next = newNode; // 将新节点插入到最后
    }
}

void destroy(LinkedList* list) {
    Node* current = list->head;
    while (current != NULL) {
        Node* temp = current; // 临时保存当前节点
        current = current->next; // 移动到下一个节点
        free(temp); // 释放当前节点的内存空间
    }
    list->head = NULL;
}

int main() {
    LinkedList list;
    init(&list);

    insert(&list, 1);
    insert(&list, 2);
    insert(&list, 3);

    Node* current = list.head;
    while (current != NULL) {
        printf("%d ", current->data); // 输出链表中的元素
        current = current->next;
    }
    printf("\n");

    destroy(&list);

    return 0;
}

以上是简单的动态分配线性表的实现示例，你可以根据自己的需求进行进一步的扩展和修改。

顺序表的实现

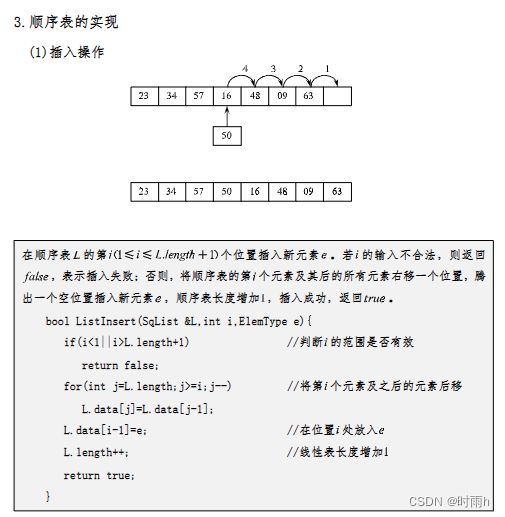
在长度为n的顺序表的第i个位置上插入一个元泰(1≤i≤n十1)，元素的移动次数为().

在长度为n的顺序表的第i个位置上插入一个元素，元素的移动次数为n - i + 1。

插入元素后，原本在第i个位置及其后面的元素都需要向后移动一位，所以移动次数为n - i。

另外，插入元素本身需要移动一次，所以总的移动次数为n - i + 1。

因此，答案是 n - i + 1。

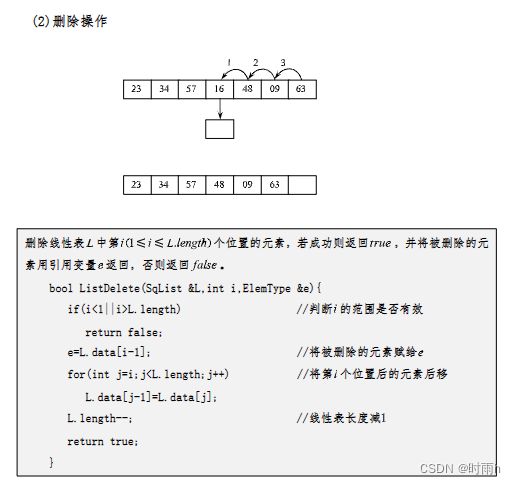
题2.设顺序线性表中有个数据元素，则删除表中第i个元素需要移动()个元素。
A.n-i
B.n-i-1
C.n-i+1
D.i
答案：A
题3.对于顺序存储的线性表，访问结点和增加、删除结点的时间复杂度为()。
A.O(n),O(n
B.O(n),O(1)
C.O(1),O(n)
D.O(1),O(1)
答案：C

题2的答案是A. n-i。

删除顺序线性表中的第i个元素时，需要将位于第i+1个位置及其后面的元素都向前移动一位，填补删除位置。因此，移动的元素个数为n-i。

题3的答案是C. O(1),O(n)。

对于顺序存储的线性表，访问结点的时间复杂度是O(1)，因为可以直接通过下标访问。

增加结点和删除结点的时间复杂度是O(n)，因为在顺序存储中，插入或删除一个元素后，需要移动该位置后面的所有元素，所以随着线性表长度的增加，时间复杂度也会增加。

按值查找操作是指在一个线性表中根据给定的值，查找该值在表中的位置或者判断该值是否存在。

具体实现方式可以是遍历整个线性表，逐个比较每个元素的值与目标值是否相等。如果找到了匹配的值，则返回其位置；如果遍历完整个表都没有找到匹配的值，则表示该值不存在。

时间复杂度为O(n)，其中n为线性表的长度。最坏情况下需要遍历整个线性表才能找到目标值或确定目标值不存在。

按位查找操作是指根据给定的位置，获取线性表中对应位置的元素值。

具体实现方式是通过索引直接访问线性表中的元素，返回对应位置的值。

时间复杂度为O(1)，因为不需要遍历整个线性表，只需要通过索引直接获取对应位置的值。

另外，对于有序线性表，可以使用二分查找来实现按值查找操作，这样可以将时间复杂度降为O(log n)，其中n为线性表的长度。具体实现方式是每次取中间位置的元素进行比较，然后根据比较结果缩小查找范围，直到找到目标元素或者确定目标元素不存在。

按位查找操作在顺序存储结构中的时间复杂度为O(1)，而在链式存储结构中时间复杂度为O(n)，其中n为链表长度。这是因为链式存储结构需要依次遍历链表中的节点才能找到目标位置。

综上所述，按值查找操作和按位查找操作都是常见的线性表操作，具体实现方式和时间复杂度取决于线性表的实现方式和特点。在实际开发中，需要根据具体情况选择合适的实现方式，以达到更高效的查找效果。

题4.将两个有序顺序表A,B合并为一个新的有序顺序表C,并用函数返回结果顺序表。

算法思想：首先，按顺序不断取下两个顺序表表头较小的结点存入新的顺序表中。然后，看哪个表还有剩余，将剩下的部分添加到新的顺序表后面。

你可以使用C语言来实现将两个有序顺序表合并为一个新的有序顺序表的算法。以下是一个示例代码：

#include 
#include 

#define MAX_SIZE 100

// 定义顺序表结构体
typedef struct {
    int data[MAX_SIZE];
    int length;
} SeqList;

// 初始化顺序表
void initSeqList(SeqList *list) {
    list->length = 0;
}

// 添加元素到顺序表
void insert(SeqList *list, int value) {
    if (list->length >= MAX_SIZE) {
        printf("顺序表已满，无法插入新元素。\n");
        return;
    }
    
    int i;
    for (i = list->length - 1; i >= 0 && list->data[i] > value; i--) {
        list->data[i + 1] = list->data[i];
    }
    
    list->data[i + 1] = value;
    list->length++;
}

// 合并两个有序顺序表
SeqList merge(SeqList listA, SeqList listB) {
    SeqList listC;
    initSeqList(&listC);
    
    int i = 0, j = 0;
    while (i < listA.length && j < listB.length) {
        if (listA.data[i] <= listB.data[j]) {
            insert(&listC, listA.data[i]);
            i++;
        } else {
            insert(&listC, listB.data[j]);
            j++;
        }
    }
    
    // 将剩余部分添加到顺序表C中
    while (i < listA.length) {
        insert(&listC, listA.data[i]);
        i++;
    }
    
    while (j < listB.length) {
        insert(&listC, listB.data[j]);
        j++;
    }
    
    return listC;
}

// 打印顺序表
void printSeqList(SeqList list) {
    printf("顺序表的元素为：");
    for (int i = 0; i < list.length; i++) {
        printf("%d ", list.data[i]);
    }
    printf("\n");
}

int main() {
    SeqList listA, listB, listC;
    initSeqList(&listA);
    initSeqList(&listB);
    
    // 向顺序表A中添加元素
    insert(&listA, 1);
    insert(&listA, 3);
    insert(&listA, 5);
    
    // 向顺序表B中添加元素
    insert(&listB, 2);
    insert(&listB, 4);
    insert(&listB, 6);
    
    // 合并两个顺序表
    listC = merge(listA, listB);
    
    // 打印合并后的顺序表C
    printSeqList(listC);
    
    return 0;
}

这段代码会将两个有序顺序表A和B合并为一个新的有序顺序表C，并通过函数返回结果顺序表。你可以根据自己的需求修改顺序表的最大长度（MAX_SIZE），及在主函数中插入元素来测试算法的正确性。