【深度学习】第三章:搭建架构-正向传播-计算损失
三、DNN架构-正向传播-计算损失
1、DNN的前生今世
DNN,全称是 deep neural network,深度神经网络。
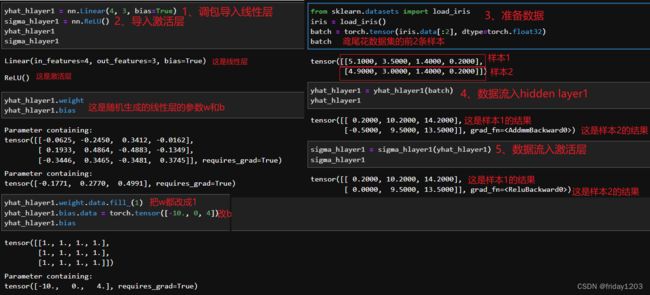
从名字上看DNN的起源就是神经网络NN(neural network),如上图A。人类大脑是最好的学习机器,所以从大脑的结构中寻找机器学习的方法也就显而易见。我们知道大脑的基本构成就是神经元,神经元通过树突接受信号,然后对信号进行加工,再通过轴突将信号传递给出去。所以我们模仿着大脑神经元的工作机制发明了感知机,如上图B。感知机是将神经元的工作方式用数学和模型的方式表达了出来。先在输入和输出之间学习一个线性关系,然后再通过激活函数进行非线性变换,得到我们想要的输出结果。上图B就是一个单层的、二分类感知机。如果把B模型用图像表达出来,就是上图的C,C中就是有4个输入,然后每个输入都通过参数w和b输出到输出层,然后再通过激活函数转化,得到一个二分类的输出。后来人们把C进行了改进,就是D,D就是一个深层神经网络,就是我们现在要讲的DNN。
这里重点给大家明确几个概念:
(1)输入层:就是上面的input layer,输入层的神经元个数是由你的数据决定的,比如前面讲的鸢尾花数据集,这个数据集有4个特征,那它对应的DNN架构的输入层一定得是4个神经元,多一个少一个都不行。
(2)隐藏层:上图的C就没有隐藏层,它是一个单层神经网络。上图的D就有一个隐藏层,它是一个两层的神经网络。所以,当我们说一个网络的层数的时候,是不包含输入层的。如果你的网络有m个隐藏层,你的网络就是一个m+1层的网络。
(3)激活函数:
一是,一般情况下激活函数是不在架构(比如上图的C,D)里面画出来的,但是有的资料里会把激活函数也画出来。即使没有画出来,你也一定要知道隐藏层后面一定是要跟激活函数的,如果隐藏层后面没有激活函数,你的多层网络就会退化成一个单层网络了。因为线性变换的叠加还是线性变换嘛。线性变换也叫仿射变换。放射变换的叠加还是放射变换。所以每层神经网络都是一个放射变换。放射变换背后的数学是矩阵的乘法,矩阵乘法又叫空间变换、空间转化等等一些很数学的概念,明白的更好,不明白的也没必要深究。说白了就是wx+b这么简单的一个线性变换。这些后面讲网络的数据流的时候你会有深刻体会的。
二是,激活函数的位置。其实激活函数可以隐藏层和输出层的前面也可以放后面。放前面叫激活函数前置,放后面叫后置。至于前置好还是后置好得看场景。后面涉及到再讲。
三是,激活函数不限于上图感知机的sign函数,还可以是sigmoid、tanh、relu等等,后面也会单独讲。
(4)参数w、b:突然发现,上图的C和D都没有画b,这是一个bug,但是懒得改了,大家凑合啊。 一是,w是必须有的,b可有可无,看你自己设置了。
二是,输入层是没有参数的,只有隐藏层和输出层才有参数,如上图的C,输出层前面的线条就是输出层的参数w,所以一个神经元就有输入个参数,如果还设置了b,一个神经元还有一个b。所以,一个隐藏层或者输出层的参数个数就是:前面一层的神经元个数x本层神经元的个数+本层神经元个数个b。这里要强调的是,参数量计算是非常重要的,你得会自己手动计算你模型的参数量。
三是,有没有发现,w和b是负责线性变换的,激活函数是负责非线性变换的。这就是为社么上面讲激活函数的时候说,如果没有激活函数,多层深究网络就退化成单层网络。也所以如果没有激活函数,神经网络就是一个线性分类器。只有加了激活函数,神经网络才拥有了非线性变换的能力。也所以这就是神经网络相比机器学习中那些算法的强大之处。这个可以参考多层神经网络-CSDN博客 这篇博文,写得非常清楚,神经网络是如何进行非线性分类的。
(5)输出层:输出层和隐藏层还是有些区别的。
首先,隐藏层的神经元个数的设置,以及激活函数的设置,目的都是为了模型有更好的效果。而输出层的神经元个数设置存粹就是为了任务目标而设置的,比如你的任务是回归类任务,那你的输出层一定得是一个神经元;如果你的任务是二分类任务,那你的输出层得是两个神经元,如上图的CD都是一个二分类模型;如果你的任务是多分类任务,那你的输出层的是类别个数个神经元。所以输出层的神经元个数是和任务关联的,不是你想设置几个就几个的。也所以隐藏层的神经元个数是和你模型的复杂程度有关的,看你数据和算力情况而设置的。
其次,输出层的激活函数可以和隐藏层的激活函数不同。一般情况下,一个网络的所有层的激活函数都只有一种激活函数。因为神经网络本来就很复杂了,不同的隐藏层再设置不同激活函数,对模型训练的稳定性、可收敛性等都不利,所以所有的隐藏层的激活函数都一样。具体你是设置sigmoid激活函数还是tanh激活函数,这个主要取决于哪个效果好就用哪个。而输出层的激活函数则不是,输出层的激活函数也是为了任务而设置。如果你是回归任务,输出层一般不要激活函数,输出层仅仅是对前面数据的一个整理汇总。如果你是二分类任务,那输出层的激活函数一般都用sigmoid+阈值判断,就是先把数据用sigmoid映射到0-1之间,然后设置一个比如0.5的阈值,大于0.5就返回1,小于0.5就返回0,就是一个0-1二分类。当然你也可以只返回sigmoid值,不用阈值判断。那此时这个返回的sigmoid值就是一个类概率值,后续用这个值来构建损失函数。如果你使用了阈值判断,这个结果后续是用来计算准确率的。这个后面还会展开讲。如果你是多分类任务,那你的输出层的激活函数一般就是softmax激活函数,返回的就是多个类别上的类概率值,后续用这个类概率值来构建损失函数的。这个后面都会演示。
(6)一般情况下,相邻两层是全连接,层内没有连接的,跨层之间也没有连接。当然如果你是分组DNN就另说了,如果你有dropout也就另说了。这里强调的主要是区别RNN的数据流,以后讲RNN时,它和DNN的区别就是数据的流向。
2、DNN架构的实现
不像机器学习,一个模型可以跑遍任何数据,深度学习的架构都是根据数据定制的。所以这里我们还以鸢尾花数据集为例。鸢尾花数据是有4个特征,3个类别的分类数据集,所以这里我们就建立一个三分类的DNN架构。
(1)架构背后的数学
神经网络的隐藏层和输出层的数学过程是:zhat = w1x1 + w2x2 +... +xnxn + b,其中,x1,x2,,xn是特征,w1,w2,,wn是模型的参数,b是截距,zhat是神经元的计算结果。
隐藏层的激活函数用relu激活函数,当然你也可以选择其他激活函数,这里我们示例就用relu。
输出层的激活函数只能用softmax函数,因为鸢尾花是个三分类数据,就是这个任务是个多分类任务,所以输出层只能是softmax激活函数。
(2)定义架构
输入层:4个神经元,因为鸢尾花数据集是4个特征的数据集。
隐藏层:这里我们打算构建两个隐藏层,第一个隐藏层打算构建3个神经元,第二个隐藏层构建2个神经元。当然这里你可以自己选择隐藏层的层数和神经元个数。这里我设置得比较保守,是因为还得画架构图,还得展示计算过程,太复杂不好展示。
输出层:3个神经元。因为鸢尾花数据集是个3分类数据集。
激活层:隐藏层都用relu激活函数,输出层使用softmax激活函数。
下图就是我们下面要搭建的架构(网络):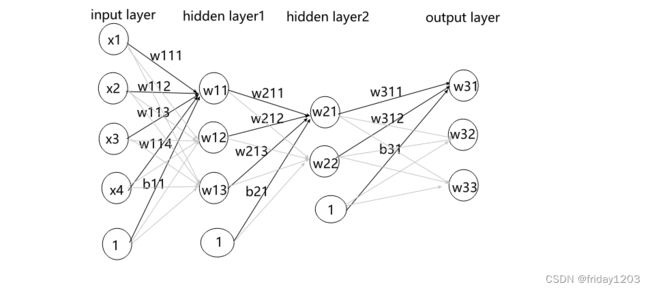
(3)手写hidden layer1层
弄明白了神经网络背后的数学,我们可以先自己手写一个层:
说明:上图A处框住的三个数字就是第一条样本的数据流过hidden layer1后,从四个特征变成了三个特征。其中第一个数字是hidden layer1的第一个神经元的输出,第二个数字是第二个神经元的输出,第三个数字是第三个神经元的输出。每个神经元都是通过wx+b算出来的结果。
同理,上图B处框住的三个数字就是第二条样本经过hidden layer1后的三个神经元的结果。
数据流过hidden layer1后,就进入hidden lyaer1后面的激活层,就是上图的步骤6。当hidden layer1的每个神经元的输出小于等于0,就把结果输出0,当输出大于0时,就把大于0的结果输出。就是上图的C和D。其中C是第一条样本经过激活函数层后的结果,D是第二条样本经过激活函数层后的结果。
说明:从结果来看,我们手写的层和掉库的层的计算结果是一样的。这里只是显示的不太一样,我手写的没有转置,pytorch中的nn.Linear()把输出结果都转了个置,这个无伤大雅哈,我实在懒得再改了。
一般情况我们是不会亲自手动完成神经网络的每一个环节的,就是不会自己去手写DNN架构的细节,这里给大家展示主要是为了展示计算过程和数据流。下面我们就用pytorch中的组件来搭建完整的架构。
小结:
(1)我们现在实现的DNN架构的每个层叫线性层。在pytorch中线性层在封装在nn.Linear(in_features, out_features, bias=True)函数里面,参数in_features表示这个层的输入数据的特征个数,参数out_features表示这个层有几个神经元,也就是这个层要输出几个特征,bias就是偏置。
(2)当我们写一个完整的架构的时候最好是写成类,而且这个类还得要继承nn.Module。
(3)在__init__函数里面一定要继承父类的的__init__,就是上图的super行。
(4)一般我们把架构写在__init__函数里。当类实例化的时候,就执行__init__()函数,此时架构里各个层的参数就被初始化了。这个初始化的参数是随机生成的。你也可以更改,更改方法上上图手动实现的过程中有更改的代码。
(5)如果激活函数是常见的函数,就不用单独写激活层了。只要在下面forward()函数中加入即可。
(6)forward函数就是数据流的传递过程。
(7)最后的softmax激活函数,一定记得参数dim否则报错。
3、DNN架构的数据流:向前传播
上图给大家详细演示了一遍数据从输入层流到输出层的全部中间过程。这个过程也叫正向传播。如果你的架构有问题,或者数据计算过程有问题,就会报错,走不通这个流程。
不但是要看懂这个传播过程,还得知道如何调取参数查看,还要知道参数结构表示什么意思,哪些参数是w哪些参数是b,这些参数又对应的是哪个层哪个神经元,也要知道数据流动过程中的计算方法,其实就是一个线性变换(矩阵乘法)+激活变换。要知道输入数据的结构,输出数据的结构和代表的意思。因为这些你都非常清楚后,后面的反向传播求梯度、参数迭代,以及最后的模型调优你就不困惑了。
4、损失函数
上图的向前传播一次,就表示我们的模型对这2条样本预测了一次。
从上图我们可以看到,我们是输入了鸢尾花数据集的前2条样本,输出的是一个2行3列的矩阵,就是上图的B处框住的矩阵。这个矩阵的行就表示样本,列表示每个样本在三种类别上的类概率值,也就是说第一条样本模型预测它是类别0的概率是0.3264,它是类别1的概率是0.3864,它是类别2的概率是0.2872。第二条样本同理。如果我们选择概率值最大的类别当作预测结果,那第一条样本的预测结果就是类别1,第二条样本的预测结果也是类别1。
我们的数据是有标签的,前面给大家展示过,前2条样本的标签都是0。所以此时我们可以计算出模型预测的准确率:0%,就是这个小批次的所有样本都预测错了。这很正常啊,因为我们模型的参数都是随机生成的初始化参数,你怎么可能指望它预测对呢。
但是,此时我们计算准确率意义不大,此时我们要构建损失函数!如何构建损失函数?我们现在的任务是一个多分类任务,就用交叉熵损失函数:
可见,交叉熵损失函数还是非常合理的。你看,第一条样本的真实标签是0,那我们是不是希望模型返回的预测值中的第一行第一列的那个类概率值尽量往1上靠,同时第一行第二列和第三列的数字尽量往0上靠。第二个样本同理。此处还需要说明的是,我们生成的B的最后一步是softmax变换,softmax变换后的每行三个数的和是1。也就是如果第一个数字尽量往1趋近,那后两个数字自然也就趋近0。也所以如果第一个数字很小,越趋近0,那第一条样本的预测损失就是极大的。如果第一个数字越趋近1,那损失就趋近0。
不同任务的损失函数不一样,这个后面我们还要单独讲损失函数,这里主要是给大家呈现一个整体过程。所以我们没单独讲nn.Linear,没有讲softmax,也没讲交叉熵损失这些点,就直接拿来用了,然后从结果推原因,这虽然有点拧巴,但为了呈现整个过程,也只能这样了,后面再点对点把这些小细节补齐。也所以这些知识点不是你用一根线就能串起来的,这些知识点之间是交织的,得从多个角度多个方面去串联。
那我们计算损失干什么?有了损失,不就可以求梯度了,求出梯度就可以更新参数了,更新参数就是模型学习了这两条样本,也就是模型训练的过程,所以下面开始讲反向传播求梯度,也就是模型的学习和训练过程。