HDOJ 3047 带权并查集

解题思路转自：

http://blog.csdn.net/azheng51714/article/details/8500459

http://blog.csdn.net/acresume/article/details/7461238

 

有一个体育馆，座位呈环状，想象下，貌似体育馆都是这样的，每一列有300个座位，按逆时钟方向编号为1~300，假设行数无穷大。

某一天，有N个人（编号为1~N）来到这个体育馆看一场赛事，主办方提出了M个要求，要求的格式是"A B X"，表示的是，假设A坐在编号为i的列，则B必须坐在编号为（i+x）%300的列上，模300是因为座位呈环状。。这些要求里有一些是错误的，只有和前面的要求产生冲突时才算错误，其它都是正确的。程序要输出错误的要求个数。

读入一个要求，看看A和B的差是否确定或是否可以根据之前的一些要求推出，即是否在同一个集合里。如果不是，则确定A和B的差，即把A所在集合和B所在集合合并为同一个集合并更新集合中每个结点相对于新根的差（查找时在路径压缩过程中分别更新两个集合的非根结点相对于根结点的差，合并时更新旧根相对于新根的差）;如果A和B已经在同一个集合里，那么判断(B-A+300)%300是否等于X，如果不相等，则该要求是错误的。另外，要注意取模操作的一些细节。

分析：这是一道比较简单地并查集题目。

（1）弄清题意，找出出现冲突的位置，判断冲突很简单就是当两个人在同一行坐，同时他们到根节点的距离差值正好是他们之间的差值，此时就出现了冲突了。

（2）关键有两个地方，这也是并查集题目的难点，就是压缩集合，和求节点到根的距离。这里压缩集合就很简单了，一个通用的递归。求到跟的距离

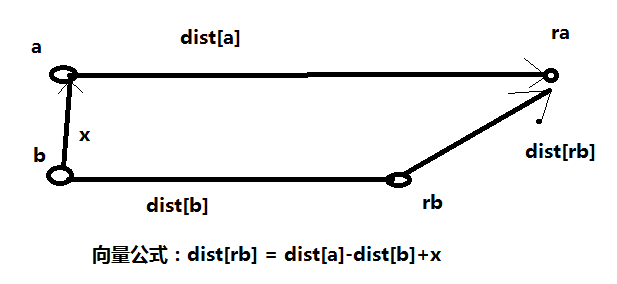
dist[a]+= dist[tem]; 

dist[rb]=dist[a]+x-dist[b];

注意这两行代码，这是核心代码，首先第一行是求出节点a到根的距离。第二行代码使用的是数学中向量计算的原理如图

AC代码：

 1 #include<iostream>

 2 #include<cstdio>

 3 #include<cstring>

 4 #include<algorithm>

 5 using namespace std;

 6 const int maxn = 200011;

 7 int n, m, root[maxn], dis[maxn];

 8 void init(){

 9     for(int i = 0; i <= n; i++)

10         root[i] = i, dis[i] = 0;

11 }

12 int find(int x){

13     if(root[x] == x)    return x;

14     int t = root[x];

15     root[x] = find(root[x]);

16     dis[x] += dis[t];//求出节点a到根的距离

17     return root[x];

18 }

19 void Union(int u,int v,int x){

20     int ru = find(u);

21     int rv = find(v);

22     root[rv] = ru;

23     dis[rv] = dis[u] + x - dis[v];//使用的是数学中向量计算

24 }

25 int main(){

26     while(scanf("%d%d",&n,&m)!=EOF){

27         init();

28         int i, j, u, v, dist, ans = 0, cnt = 0;

29         while(m--){

30             scanf("%d%d%d",&u,&v,&dist);

31             if(find(u) != find(v))    Union(u,v,dist);

32             else if(dis[u] + dist != dis[v])    ans++;

33         }

34         printf("%d\n",ans);

35     }

36     return 0;

37 }

 

Zjnu Stadium

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1221    Accepted Submission(s): 472

Problem Description

In 12th Zhejiang College Students Games 2007, there was a new stadium built in Zhejiang Normal University. It was a modern stadium which could hold thousands of people. The audience Seats made a circle. The total number of columns were 300 numbered 1--300, counted clockwise, we assume the number of rows were infinite.
These days, Busoniya want to hold a large-scale theatrical performance in this stadium. There will be N people go there numbered 1--N. Busoniya has Reserved several seats. To make it funny, he makes M requests for these seats: A B X, which means people numbered B must seat clockwise X distance from people numbered A. For example: A is in column 4th and X is 2, then B must in column 6th (6=4+2).
Now your task is to judge weather the request is correct or not. The rule of your judgement is easy: when a new request has conflicts against the foregoing ones then we define it as incorrect, otherwise it is correct. Please find out all the incorrect requests and count them as R.

 

Input

There are many test cases:
For every case:
The first line has two integer N(1<=N<=50,000), M(0<=M<=100,000),separated by a space.
Then M lines follow, each line has 3 integer A(1<=A<=N), B(1<=B<=N), X(0<=X<300) (A!=B), separated by a space.

 

Output

For every case:
Output R, represents the number of incorrect request.

 

Sample Input

10 10 1 2 150 3 4 200 1 5 270 2 6 200 6 5 80 4 7 150 8 9 100 4 8 50 1 7 100 9 2 100

 

Sample Output

2

Hint

Hint: （PS： the 5th and 10th requests are incorrect）