梯度上升和随机梯度上升
目录
梯度上升算法:
代码:
随机梯度上升算法:
代码:
实验:
做图代码:
疑问:
1.梯度上升算法不适应大的数据集,改用随机梯度上升更合适。
2.改进过的随机梯度算法,w vs epoch曲线出现波动。
代码实现时遇到的问题
1.对随机的理解,随机过的样本不再参与随机?
2.数组越界
实验结果:
Logistic回归实现二分类:http://t.csdnimg.cn/eEEjF
学习资料:Peter Harrington 机器学习实战
梯度上升算法:
如下,每更新一次权重需要计算所有样本(train_X)和权重乘积的sigmoid值。
对于m行n列特征矩阵和n行权重,迭代次数epoch,计算复杂度为O(n*m*epoch),w迭代次数为epoch.
代码:
def grad(train_X,train_y):
# 100*3
m,n = len(train_X[:,0]),len(train_X[0])
#3x1
weight=np.ones((n,1))
#迭代系数
epoch=500
for i in range(epoch):
# mxn nx1 ->m*1
y_=sigmoid(np.dot(train_X,weight))
# m*1
loss = train_y -y_
a = 0.01
# 3*1
weight = weight - np.dot(a*train_X.transpose(),loss)
return weight随机梯度上升算法:
每计算一次样本更新一次权重。
代码:
def grad(train_X,train_y):
# 100*3
m,n = len(train_X[:,0]),len(train_X[0])
#3x1
weight=np.ones((n,1))
# 每个样本更新权重一次,故使用m
for i in range(m):
# mxn nx1 ->m*1
# y_=sigmoid(np.dot(train_X,weight))
# 1xn nx1 -->1x1
#(3,)表示只有一个维度,在这个维度上有三个数字
y_=sigmoid(sum(np.dot(train_X[i].reshape(1,n),weight)))
# 1x1
loss = train_y[i] -y_
a = 0.01
# nx1 1xn 1x1 nx1 1x1
weight = weight + a*np.dot(train_X[i].transpose().reshape(n,1),loss.reshape(1,1))
return weight使用这种方法实现的分类效果相较之前效果变差了,应该是w迭代次数不够,为了查看何时收敛,查看w和epoch的变化关系图。
| 梯度上升 | 随机梯度上升 |
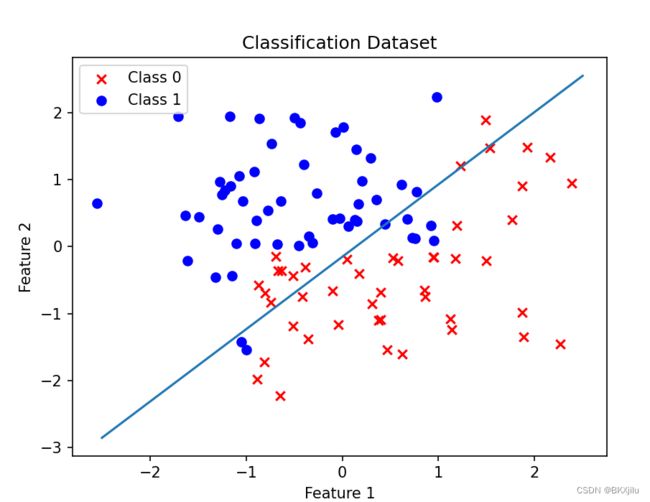 |
 |
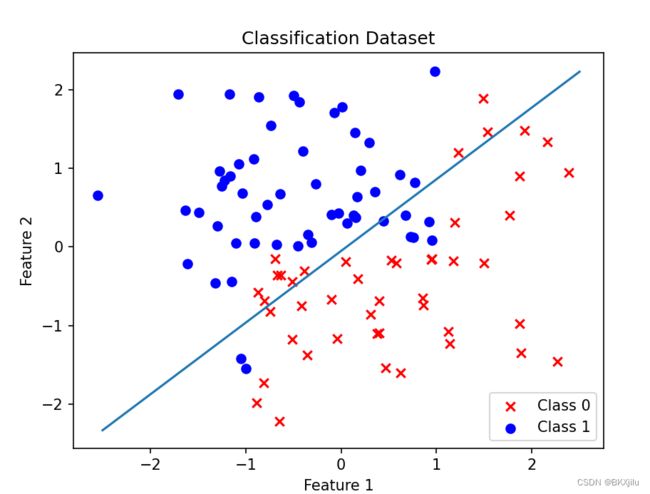
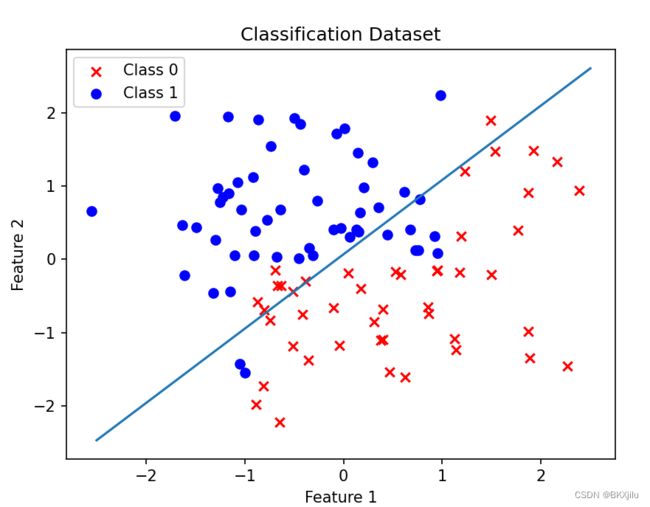
实验:
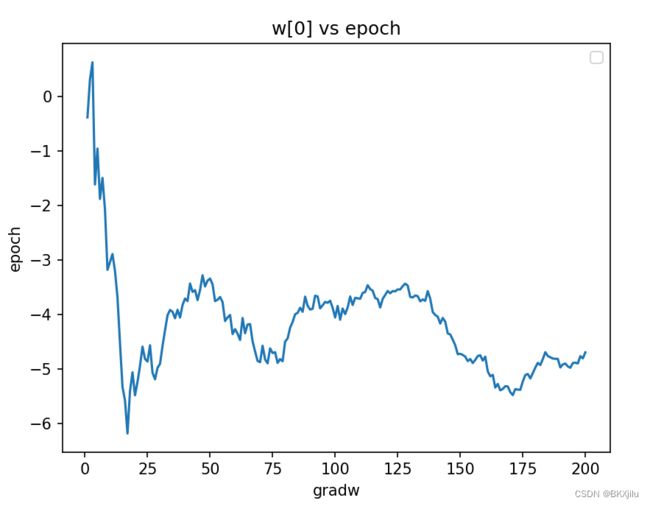
使用随机梯度算法:研究w和epoch的关系,epoch表示迭代数据集的次数.
![]()
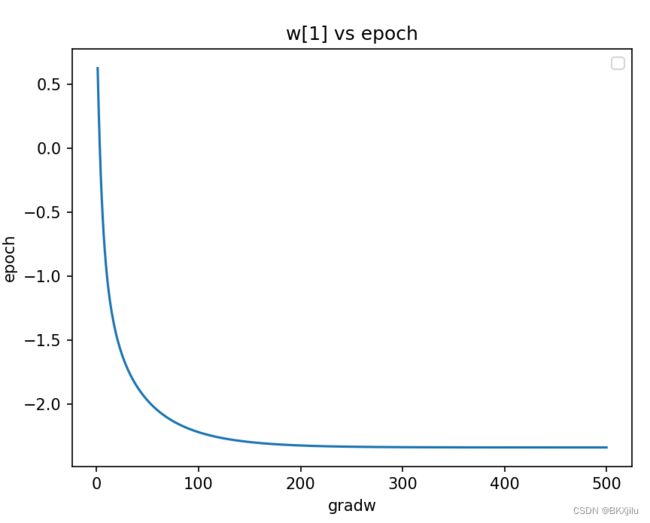
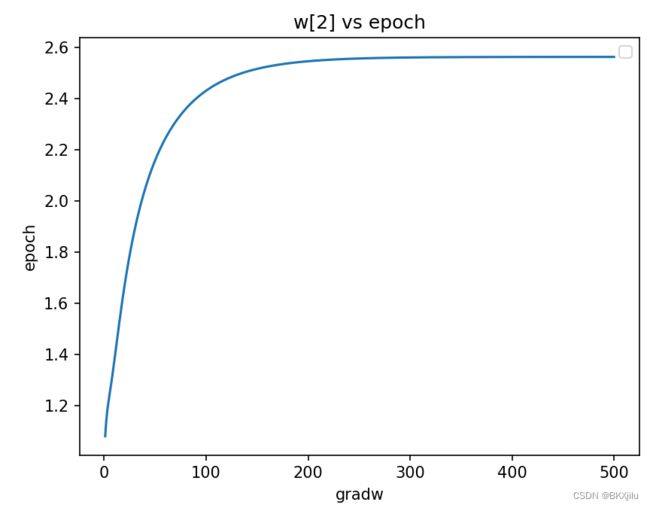
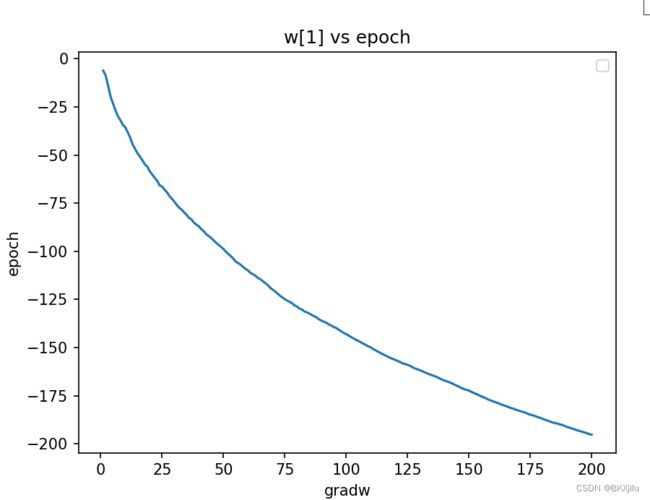
![]() 分别为权重为w[0],w[1],w[2]。
分别为权重为w[0],w[1],w[2]。
可以看出w0收敛很快,w1和w2需要更多时间才能实现收敛.
发现w大概到epoch=200处收敛,设置遍历数据集200次得到新图像基本和梯度算法基本一致:
做图代码:
def grad(train_X,train_y):
# 100*3
m,n = len(train_X[:,0]),len(train_X[0])
#3x1
weight=np.ones((n,1))
#迭代系数
epoch=500
w=[]
# lineArr.append(float(currLine[i]))
#100x100次
for j in range(epoch):
for i in range(m):
# mxn nx1 ->m*1
# y_=sigmoid(np.dot(train_X,weight))
# 1xn nx1 -->1x1
#(3,)表示只有一个维度,在这个维度上有三个数字
y_=sigmoid(sum(np.dot(train_X[i].reshape(1,n),weight)))
# 1x1
loss = train_y[i] -y_
a = 0.01
# nx1 1xn 1x1 nx1 1x1
weight = weight + a*np.dot(train_X[i].transpose().reshape(n,1),loss.reshape(1,1))
w.append(weight)
w0=[row[0] for row in w]
w1=[row[1] for row in w]
w2=[row[2] for row in w]
epochlist =list(range(1,epoch+1,1))
plt.plot(epochlist,w0)
plt.xlabel('gradw')
plt.ylabel('epoch')
plt.legend()
plt.title("w[0] vs epoch")
plt.show()
plt.plot(epochlist,w1)
plt.xlabel('gradw')
plt.ylabel('epoch')
plt.legend()
plt.title("w[1] vs epoch")
plt.show()
plt.plot(epochlist,w2)
plt.xlabel('gradw')
plt.ylabel('epoch')
plt.legend()
plt.title("w[2] vs epoch")
plt.show()
return weight疑问:
1.梯度上升算法不适应大的数据集,改用随机梯度上升更合适。
书中提到:数据量大的话不太方便,所以想到每计算一次样本更新一次权重,也就是随机梯度上升算法。但是计算每个样本迭代的权重,再遍历全部样本,不就是把矩阵乘法拆开算吗,我不理解,感觉没有提升运算效率的作用。
2.改进过的随机梯度算法,w vs epoch曲线出现波动。
我感觉这个第一个随机梯度上升法完全没有体现随机性,随机应该随机抽取训练集的的子集来更新回归系数吧。
书里有提到随机梯度算法的改进:
2.1.学习率随着迭代次数增加应该减小,能缓解高频波动。(不过我的实验在第一个梯度上升没有出现高频波动,改进后反而出现了。)
2.2.随机抽取样本进行类别预测,loss计算和更新权重。
randIndex是0-len(dataIndex)的随机值;去掉dataIndex[randIndex]的值
但是这个randIndex和dataIndex为什么这么写,不太理解.
def grad(train_X,train_y):
m,n = len(train_X[:,0]),len(train_X[0])
weight=np.ones((n,1))
epoch=50
w=[]
for j in range(epoch):
#[0,1,2,,,m-1]对应train_X的索引
dataIndex = list(range(m))
for i in range(m):
#随着迭代次数增加,减小学习率
alpha = 4/(1.0+j+i)+0.0001
#在dataIndex中取随机样本的索引
randIndex = int(random.uniform(0,len(dataIndex)))
y_=sigmoid(sum(np.dot(train_X[randIndex].reshape(1,n),weight)))
loss = train_y[i] -y_
weight = weight + alpha*np.dot(train_X[i].transpose().reshape(n,1),loss.reshape(1,1))
#去掉计算过的样本
del(dataIndex[randIndex])
return weight代码实现时遇到的问题
1.对随机的理解,随机过的样本不再参与随机?
从dataIndex中随机取值,作为随机数;去掉dataIndex中被选过的值,即随机过的样本不再参与随机了。
randIndex = random.choice(dataIndex)
dataIndex.remove(randIndex)2.数组越界
代码错误:取0-len(dataIndex)的值作为索引,拿到randIndex的随机值;但是去掉索引为randIndex对应的值
dataIndex=[0,1,2,,,80] len=81 假设去掉了dataIndex[79]=79,
dataIndex=[0,1,2,,,78,80] len=80 取79 randIndex=dataIndex[79]=80 去掉randIndex[80]数组越界
就可能出现越界:
randIndex = dataIndex[int(random.uniform(0,len(dataIndex)))]
del(dataIndex[randIndex])实验结果:
w和epoch关系: