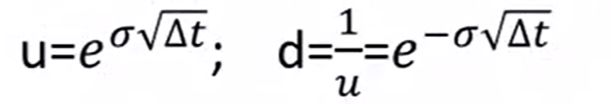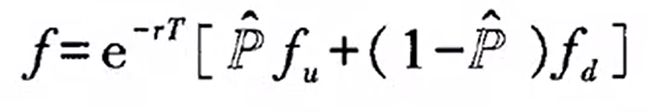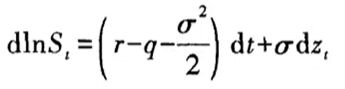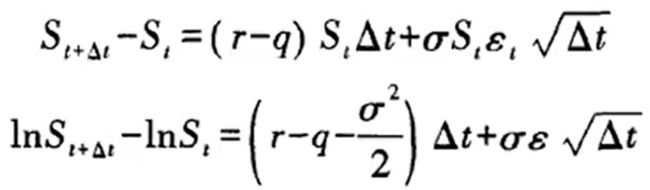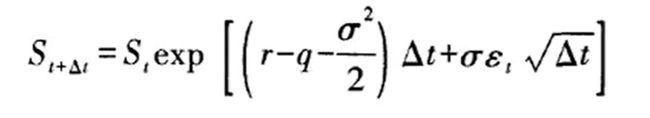创帆云

期权的定义与BSM定价

期权定价模型

期权定义

期权，是指一种合约，源于十八世纪后期的美国和欧洲市场，该合约赋予持有人在某一特定日期或该日之前的任何时间以固定价格购进或售出一种资产的权利。期权定义的要点如下：

1、期权是一种权利，期权合约至少涉及买家和出售人两方。持有人享有权利但不承担相应的义务。

2、期权的标的物。期权的标的物是指选择购买或出售的资产。它包括股票、政府债券、货币、股票指数、商品期货等。期权是这些标的物“衍生”的，因此称衍生金融工具。值得注意的是，期权出售人不一定拥有标的资产。期权是可以“卖空”的。期权购买人也不一定真的想购买资产标的物。因此，期权到期时双方不一定进行标的物的实物交割，而只需按价差补足价款即可。

3、到期日。双方约定的期权到期的那一天称为“到期日”，如果该期权只能在到期日执行，则称为欧式期权；如果该期权可以在到期日及之前的任何时间执行，则称为美式期权。

4、期权的执行。依据期权合约购进或售出标的资产的行为称为“执行”。在期权合约中约定的、期权持有人据以购进或售出标的资产的固定价格，称为“执行价格”。

期权价格特性

内在价值与时间价值

期权价格（或者说价值）=期权的内在价值+时间价值。

期权的内在价值，是多方可能行使期权时所获回报最大贴现的较大值。看涨期权的“所获回报”为St-X，看跌期权为X-St ，这里的T是指多方行使期权的时刻。由于欧式期权和美式期权可执行的时间不同，其内在价值的计算也就有所差异。

【

附：欧式期权和美式期权的区别

行权时间不同

欧式期权只能在合同约定的到期日行权，美式期权可以在到期日以及到期日之前的任何时间点行权，即美式期权意味着持有者有更高的自由度，更大的选择权。

在其他条件相同的情况下，美式期权的价值≥欧式期权的价值

期权价值=期权内在价值+时间价值

期权内在价值是指假设当前立即决定行权或弃权的期权价值，实际上是当前时点的净收入。影响期权内在价值的因素包括两项，一是执行价格，二是现行股价。

以看涨期权（买权）为例，当现行股价大于执行价格时，站在当前时点，立即行权可获利，期权内在价值=现行股价-执行价格，此时期权处于实值状态（溢价）；当现行股价等于执行价格时，立即行权无意，持有者不会选择立即行权，期权的内在价值为0，此时，期权处于平价状态；当现行股价小于执行价格时，立即行权受损，持有者不会选择行权，期权内在价值为0，此时期权处于虚值状态。

不管是看涨期权还是看跌期权，期权的内在价值都是非负的。

时间价值也称为时间溢价，由于市场股价未来的变化增加了期权价值的可能性，对于美式期权而言，可行权时间越长，期权的时间溢价越高，期权的时间价值=期权价值-内在价值；期权到期日，期权的时间价值为0，期权价值=内在价值。

在其他条件均相等的情况下，美式期权由于在到期日以及到期日之前均可以选择行权或不行选，选择机会大于欧式期权，同等条件下，美式期权的时间溢价大于等于欧式期权的时间溢价。

一般情况下，其他条件相同情况下，美式期权的期权价格≥欧式期权的期权价格

期权价格（权利金）是期权持有人为了获得期权（选择权）而付出的成本，价值决定价格，价格是价值的外在表现形式，价格围绕价值上下波动。因美式期权价值≥欧式期权价值，所以一般情况下，在其他条件相同的情况下，美式期权的期权价格≥欧式期权的期权价格。

】

实值期权、平值期权与虚值期权

与期权内在价值紧密联系的几个概念是期权的平值点以及对应的实值期权，平值期权与虚值期权。所谓平值点，就是使得期权内在价值由正值变化到零的标的资产价格的临界点。

三者区别：

实值期权In-the-Money (ITM)：行权价格小于标的资产当前价格的看涨期权，或行权价格大于标的资产当前价格的看跌期权。

平值期权At-the-Money (ATM)：行权价格等于标的资产当前价格的看涨期权和看跌期权。

虚值期权Out-of-the-Money (OTM)：行权价格大于标的资产当前价格的看涨期权，或行权价格小于标的资产当前价格的看跌期权。

期权的时间价值

期权的时间价值是基于期权多头权利义务不对称这一特性，在期权到期前，标的资产价格的变化可能给期权多头带来的收益的一种反映。

期权价格影响因素

期权价格由内在价值和时间价值两部分构成，但凡是影响内在价值和时间价值的因素，就是影响期权价格的因素。总的来看，期权价格的影响因素主要有以下几个，它们通过影响期权的内在价值和时间价值来影响期权的价格。

说明：

在期权价值的基础上，市场对期权合约的供需关系决定了期权的市场价格，即权利金。从期权要素来看，期权价格通常会受到标的价格、行权价、合约到期期限、市场无风险利率、标的证券价格波动率等因素的影响。

（1）期权标的价格。标的价格上涨，则认购期权价格上涨，而认沽期权价格下跌。对于前述行权价格为65元的认购期权来说，如果标的价格从63元上涨到68元，那么合约就从虚值变成了实值，因此期权的价格也会相应上涨。而对于同样行权价格为65元的认沽期权来说，如果标的价格从63元涨到68元，期权就从实值变成了虚值，其价格会下跌。

（2）期权的行权价。行权价越高，认购期权的价格越低，认沽期权的价格越高。行权价为55元的认购期权比65元的认购期权贵，这是因为期权买方可以以更优越的价格买入标的证券。同样的道理，行权价为75元的认沽期权比65元的认沽期权贵，因为期权买方可以以更高的价格卖出标的证券。

（3）期权的合约到期期限。对于期权来说，期权到期期限越长，期权买方获利的可能性越大，期权卖方须承担的风险也越大，因此期权价格越高。从另外一个角度看，期权到期期限越长，期权的时间价值也就越高。如果把期权比作保险，保险时间越长，所支付的保险费理应越高。

（4）期权的市场无风险利率。认购期权具有融资买入标的证券的性质，市场无风险利率越高，意味着融资成本越高，认购期权的价格就越高。同理，买入认沽期权可以达到卖空标的证券的效果。如果单纯卖空标的证券，投资者将获得现金收入，而买入认沽期权是没有现金收入的。市场无风险利率越高就越不利于认沽期权投资者，因此认沽期权的价格就越低。

（5）期权标的证券价格波动率。标的证券价格的波动率是用来衡量标的证券未来价格变动不确定性的指标。简单地说，标的证券价格波动率越高，期权合约到期时成为实值期权的可能性就越高，因此相应合约具有更高的价格。波动率分为历史波动率和隐含波动率。

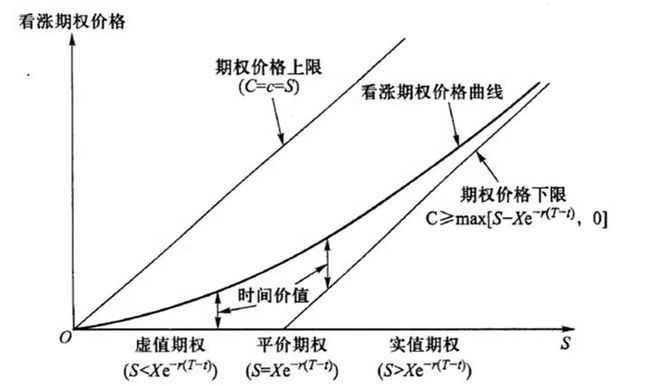
期权价格曲线

看涨期权价格曲线

期权价格等于内在价值+时间价值。内在价值主要取决于S和X，而时间价值由取决于内在价值、无风险利率、波动率等因素，因此可以得到下面的期权价格曲线：

看跌期权价格曲线

BSM定价模型

不分红股票的期权定价模型-BSM

BSM（black-scholes-merton）模型假设标的股票在到期日前不支付任何股息，因而给出了欧式期权价格的解析表达式。如果用S0代表当前价格，X代表行使价，r代表连续得利的无风险利率，T代表以年为单位的期权有效期，σ代表股票的波动率，N（）是累计标准正态分布函数，那么欧式看涨期权（C）的价格公式和欧式看跌期权（P）的价格公式分别如下：

已知分红股票的欧式期权价格

假设期权的到期日是T，已知标的股票在时间T1将发放红利，T1

BSM 期权定价模型在 Python 中的实现

from scipy import log,exp,sqrt,stats

def bs_call (S,X,T,r,sigma ) :

dl=(log(S/X) + (r+sigma*sigma/2.)*T)/(sigma*sqrt(T))

d2=d1-sigma*sqrt (T)

return S*stats.norm.cdf (dl)-X*exp(-r*T)*stats.norm.cdf(d2)

s0=40;r=0.1; T=0.5;X=42; sigma=0.2

bs_call(s0,X, T, r, sigma)

d=1.5

s=s0-exp(-r*T*d)

bs_call(s,X, T,r,sigma)

二叉树法

二叉树法（CRR法）由CR和Robin在1979年提出，二叉树图方法用离散的模型模拟资产价格的连续运动，利用均值和方差匹配来确定相关参数，然后从二叉树图的末端开始倒推可以计算出期权价格。

应用多步二叉树模型来表示证券价格变化的完整树形结构，其中u>1,d<1。

得到每个节点的资产价格之后，就可以在二叉树模型中采用倒推定价法，从树形结构图的末端t时刻开始往回折现，主期权定价。

用于计算u、d和P的公式如下:

其中每一步上升的概率：

得到风险中性概率以后每一步期权的价格为：

二叉树定价—欧式看涨期权在 Python 中的实现

from math import exp,sqrt

import scipy as sp

def binomialCall(s,x,T,r,sigma,n=1000):

deltaT=T/n

u=exp(sigma*sqrt(deltaT))

d=l/u

a=exp(r*deltaT)

p=(a-d)/(u-d)

v=[[0.0 for j in sp.arange(i+l)J for i in sp.arange(n+l)

for j in sp.arange(n+l):

v[n][j]J=max(s*u**j*d**(n-j)-x,0.0)

for i in sp.arange(n-l,-1,-1):

for j in sp.arange(i+l):

v[i][j]=exp(-r*deltaT)*(p*v[i+l][j+l]+(1-p)*v[i+l][j])

return v[0][0]

binomia1Call(40,42,0.5,0.1,0.2,1000)

二叉树—美式看涨期权在 Python 中的实现

def binomialCallAmerican(s,x, T ,r, sigma,n=1000):

deltaT=T/n

u=exp(sigma*sqrt(deltaT))

d=l/u

a=exp(r*deltaT)

p=(a-d)/(u-d)

v=[[0.0 for j in sp.arange(i+1)] for i in sp.arange(n+l)]

for j in sp.arange(n+l):

v[n][j]=max(s*u**j*d**(n-j)-x,0.0)

for i in sp.arange(n-1, -1, -1):

for j in sp.arange(i+l):

vl=exp(-r*deltaT)*(p*v[i+l][j+l]+(1-p)*v[i+l][j])

v2=max(x-s,0)

v[i][j]=max(vl,v2)

return v[0][0]

call=binomialCallAmerican(40,42,0.5,0.1,0.2,1000)

round(call,2)

蒙特卡罗模拟与期权定价

概述

蒙特卡罗模拟，是一种通过模拟标的资产价格的随机运动路径得到期权价值期望值的数值方法，也是一种应用十分广泛的期权定价方法。由于风险中性定价法可以使问题大大简化，因此主要介绍在风险中性世界中的蒙特卡罗模拟，其基本原理也适用于现实世界。

基本过程

在风险中性世界中，蒙特卡罗模拟期权定价法的基本思路是：由于大部分期权（如欧式期权）价值等于期权到期回报的期望值的贴现，因此先模拟风险中性世界中标的资产价格的多种运动路径，然后计算所有路径结果下的期权回报均值，最后用无风险利率贴现就可以得到期权价值。

以一个简单的欧式期权F（St,t）(即只有两个状态变量，资产价格St和时间t，且利率为常数)为例，可以说明蒙特卡罗模拟的基本方法：

从初始时刻的标的资产价格开始，直至到期为止，为St取一条在风险中性世界中跨越整个有效期的随机路径，这是众多路径中的一条。
计算出这条路径下期权的回报。
重复上面两个步骤，得到许多样本结果，即风险中性世界中期权回报的大量可能取值。
计算这些样本回报的均值，得到风险中性世界中预期的期权回报值。
用无风险利率贴现，得到这个期权的当前估值。

技术实现

在风险中怀世界中，服从几何布朗运动且连续收益率为q的标的资产价格所遵循的随机过程可以写作：

也可以写作：

为了模拟St的路径，我们把期权的有效期分为N个长度为Δt的时间段。

由上面的近似方程分别为：

还可以写为：

式中St是t时刻S的价值：

ε是从标准正态分布中抽取的一个随机样本。因此，蒙特卡罗模拟就是离散地模拟资产价格St的时间序列，这样，只要得知初始时刻t的St值，随机抽取一个εt,就能算出Δt时刻的价值St+Δt,接着2Δt时的值又能从Δt时的St+Δt值计算得到。因此，通过N个正态分布的随机取样就可以组建一条资产价格的蒙特卡罗模拟样本路径，并得到相应的回报值。重复以上的模拟至足够多的次数，计算回报值的平均值，折现后就得到了期权的估值，另外也可以顺便得到所估计期权的标准差。

代码模拟定价

假设有一份期限为六个月的股票期权，标的资产股票价格为 5.29 元，期权执行价格为 6 元，

年化无风险利率和年化波动率分别为 4%和 24%，用蒙特卡洛模拟法求看涨期权和看跌期权

的价格（模拟 1 万次）。

import numpy as np

from numpy.random import standard_normal

def callMonteCarlo(S,X,r,sigma,t,n):

z=standard_normal(n)

St=S*np.exp((r-0.5*sigma**2)*t+sigma*z*np.sqrt(t))

return sum(np.maximum(0,St-X))*(np.exp(-r*t))/n

def putMonteCarlo(S,X,r,sigma,t,n):