第16章 局部波动率模型——对冲比率及奇异期权估值
这学期会时不时更新一下伊曼纽尔·德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思路不一定够清晰且由于分工原因我是从书本第13章写起,还请大家见谅。
第16章 局部波动率模型——对冲比率及奇异期权估值
局部波动率模型中的对冲比率
之前已经证明,对于一个标准期权,BSM模型中的隐含波动率可以看作在当前股票价格和到期日行权价之间的局部波动率的平均值,可以用一个线性函数近似表达局部波动率和标的股票价格之间的关系。如果隐含波动率等于局部波动率的平均数,股票价格发生微小变动导致隐含波动率发生的变动幅度,就应该近似等于由行权价格变动导致隐含波动率发生的变动幅度,即:
∂ ∂ S Σ ( S , t , K , T ) ≈ ∂ ∂ K Σ ( S , t , K , T ) \frac{\partial}{\partial S}\Sigma(S,t,K,T)\approx\frac{\partial}{\partial K}\Sigma(S,t,K,T) ∂S∂Σ(S,t,K,T)≈∂K∂Σ(S,t,K,T)
为了证明该关系式成立,我们可以将局部波动率表示为:
σ ( S ) = σ 0 − 2 β ( S − S 0 ) \sigma(S)=\sigma_0-2\beta(S-S_0) σ(S)=σ0−2β(S−S0)
其中 σ ( S ) \sigma(S) σ(S) 与时间无关,当股价等于 S 0 S_0 S0 时,局部波动率等于 σ 0 \sigma_0 σ0
对于一个行权价为 K K K 的期权来说,其隐含波动率 Σ ( S , K ) \Sigma(S,K) Σ(S,K) 约等于 S S S 和 K K K 之间的局部波动率 σ ( S ) \sigma(S) σ(S) 的平均值,即:
Σ ( S , K ) ≈ 1 2 [ ( σ 0 − 2 β ( S − S 0 ) ) + ( σ 0 − 2 β ( K − S 0 ) ) ] ≈ σ 0 + 2 β S 0 − β ( S + K ) \Sigma(S,K)\approx\frac{1}{2}[(\sigma_0-2\beta(S-S_0))+(\sigma_0-2\beta(K-S_0))]\\\approx\sigma_0+2\beta S_0-\beta(S+K) Σ(S,K)≈21[(σ0−2β(S−S0))+(σ0−2β(K−S0))]≈σ0+2βS0−β(S+K)
同时对 S , K S,K S,K 求导数可得
∂ ∂ S Σ ( S , K ) = ∂ ∂ K Σ ( S , K ) ≈ − β \frac{\partial}{\partial S}\Sigma(S,K)=\frac{\partial}{\partial K}\Sigma(S,K)\approx-\beta ∂S∂Σ(S,K)=∂K∂Σ(S,K)≈−β
因此,如果局部波动率对标的股票价格的斜率等于 2 β 2\beta 2β,那么隐含波动率对行权价格和股票价格的斜率就等于 β \beta β。局部波动率随股票价格变动的速度等于隐含波动率随行权价格变动速度的两倍
普通期权的正确对冲比率
根据局部波动率模型,我们可以找到一个期权的正确对冲比率,这需要计算BSM公式下的期权价格 C B S M ( S , Σ ) C_{BSM}(S,\Sigma) CBSM(S,Σ) 的全导数:
Δ ≡ d C B S M d S = ∂ C B S M ∂ S + ∂ C B S M ∂ Σ ∂ Σ ∂ S Δ ≈ Δ B S M − V B S M β \Delta\equiv\frac{dC_{BSM}}{dS}=\frac{\partial C_{BSM}}{\partial S}+\frac{\partial C_{BSM}}{\partial\Sigma}\frac{\partial\Sigma}{\partial S}\\ \Delta\approx\Delta_{BSM}-V_{BSM}\beta Δ≡dSdCBSM=∂S∂CBSM+∂Σ∂CBSM∂S∂ΣΔ≈ΔBSM−VBSMβ
其中 Δ B S M \Delta_{BSM} ΔBSM 和 V B S M V_{BSM} VBSM 分别表示BSM模型中的delta和vega,而 β \beta β 跟之前一样表示隐含波动率函数的负斜度值。对于标准看涨期权和看跌期权而言, V B S M V_{BSM} VBSM 是正数;因此,当隐含波动率斜度为负的时候,标准期权的对冲比率会小于 Δ B S M \Delta_{BSM} ΔBSM
案例:
假设欧洲斯托克 50 指数 (SX5E) 的局部波动率服从下列等式:
σ ( S ) = σ 0 − 2 β ( S − S 0 ) = 0.2 − 2 × 0.00005 × ( S − 3000 ) \sigma(S)=\sigma_0-2\beta(S-S_0)=0.2-2\times0.00005\times(S-3000) σ(S)=σ0−2β(S−S0)=0.2−2×0.00005×(S−3000)
SX5E当前的价格水平是 S = S 0 = 3000 S=S_0=3000 S=S0=3000。假设有一个以SX5E为标的资产的1年期欧式看涨期权,行权价为3300,请问其对冲比率是多少?假设股息率和无风险利率都等于0。答案:
Σ ( S , K ) = σ 0 + 2 β S 0 − β ( S + K ) = 0.2 + 2 × 0.00005 × 3000 − 0.00005 × ( 3000 + 3300 ) = 0.2 + 0.00005 × ( 6000 − 6300 ) = 0.2 − 0.00005 × 300 = 0.185 \Sigma(S,K)=\sigma_0+2\beta S_0-\beta(S+K)\\=0.2+2\times0.00005\times3000-0.00005\times(3000+3300)\\=0.2+0.00005\times(6000-6300)\\=0.2-0.00005\times300=0.185 Σ(S,K)=σ0+2βS0−β(S+K)=0.2+2×0.00005×3000−0.00005×(3000+3300)=0.2+0.00005×(6000−6300)=0.2−0.00005×300=0.185
要计算BSM模型下的 delta 值和 vega 值,我们首先需要计算 d 1 d_1 d1:
v = σ τ = 0.185 d 1 = 1 v ln ( S K ) + v 2 = 1 0.185 ln ( 3000 3300 ) + 0.185 2 = − 0.4227 v=\sigma\sqrt{\tau}=0.185\\ d_1=\frac{1}{v}\ln(\frac{S}{K})+\frac{v}{2}=\frac{1}{0.185}\ln(\frac{3000}{3300})+\frac{0.185}{2}=-0.4227 v=στ=0.185d1=v1ln(KS)+2v=0.1851ln(33003000)+20.185=−0.4227
BSM模型中各项参数值就等于:
Δ B S M = N ( d 1 ) = 0.34 V B S M = S τ 2 π e − 1 2 d 1 2 = 1095 \Delta_{BSM}=N(d_1)=0.34\\ V_{BSM}=\frac{S\sqrt{\tau}}{\sqrt{2\pi}}e^{-\frac{1}{2}d_1^2}=1095 ΔBSM=N(d1)=0.34VBSM=2πSτe−21d12=1095
于是有:
Δ ≈ Δ B S M − V B S M β ≈ 0.34 − 1095 × 0.00005 = 0.28 \Delta\approx\Delta_{BSM}-V_{BSM}\beta\approx0.34-1095\times0.00005=0.28 Δ≈ΔBSM−VBSMβ≈0.34−1095×0.00005=0.28
正确的对冲比率约等于0.28,显著低于BSM模型中的对冲比率0.34
局部波动率下奇异期权的理论价值
以障碍期权和回望期权为例,分析局部波动率模型对奇异期权估值的影响
上升出局看涨期权,行权价=100美元,障碍价=110美元
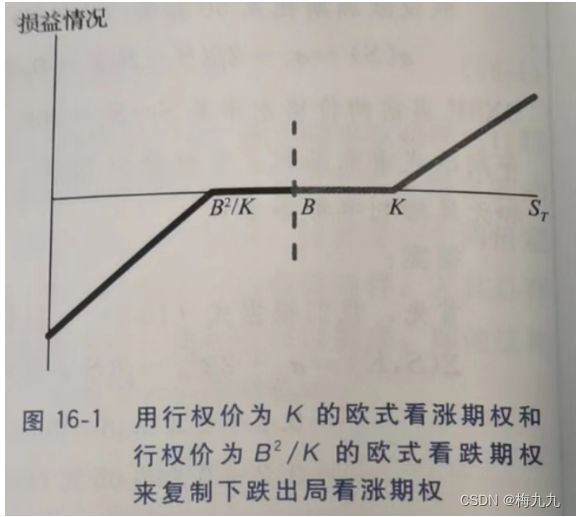
之前已经证明过, 可以用一个欧式损益的衍生品来近似复制一个下跌出局看涨期权,如下图所示
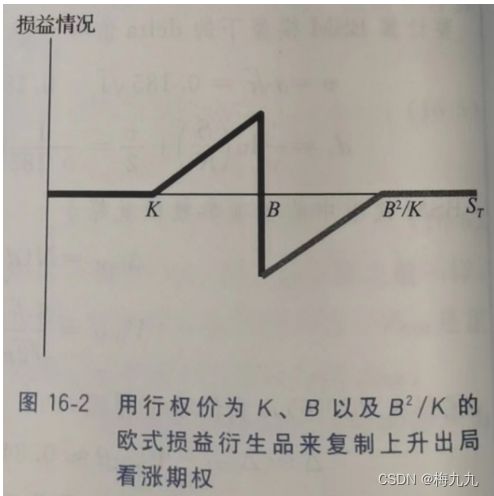
与此相似,下图展示了如何用一个欧式损益的衍生品来近似复制一个上升出局看涨期权,注意,在到期日前,如果股价触及障碍价 B B B,那么该欧式损益衍生品的价值就约等于0
该衍生品在 K K K 点的曲率为正,这相当于买入一个行权价为 K K K 的看涨期权,在 B 2 / K B^2/K B2/K 点的曲率为负,这相当于卖出一个行权价为 B 2 / K B^2/K B2/K 的看跌期权。此外,在障碍价 B B B 点,损益的曲率大幅变化,从负转正。在水平波动率的情况下,这样的欧式损益衍生品的价值是由 BSM 的常数波动率决定的
在倾斜波动率的情况下已经证明过,一个标准欧式期权的隐含波动率约等于当前股票价格和行权价格之间的局部波动率的平均值。一个标准欧式期权的曲率在行权价附近时是最大的。如果是更广义上的欧式损益衍生品,没有单一的行权价,就应该计算当前股价水平以及曲率较大的价格水平之间局部波动率的平均值,在这个案例中曲率较大的价格水平即为 K , B , B 2 / K K,B,B^2/K K,B,B2/K
对于行权价为 100 美元,障碍价为 110 美元的上升出局看涨期权来说, B 2 / K B^2/K B2/K 约等于120美元,高于行权价本身。因此在局部波动率模型中,上升出局看涨期权的BSM隐含波动率就约等于 100 美元和120美元之间的局部波动率的平均值
在上图中,该区域内的局部波动率范围是10%和7%,其平均值就约等于8.5%。假设无风险利率等于5%,根据局部波动率二叉树模型,在80个时间间隔周期下,一个1年期上升出局看涨期权的价值约为1.10美元,这跟 BSM 隐含波动率为 8.5%的期权价格很接近
没有布莱克-斯科尔斯-默顿隐含波动率的上升出局看涨期权
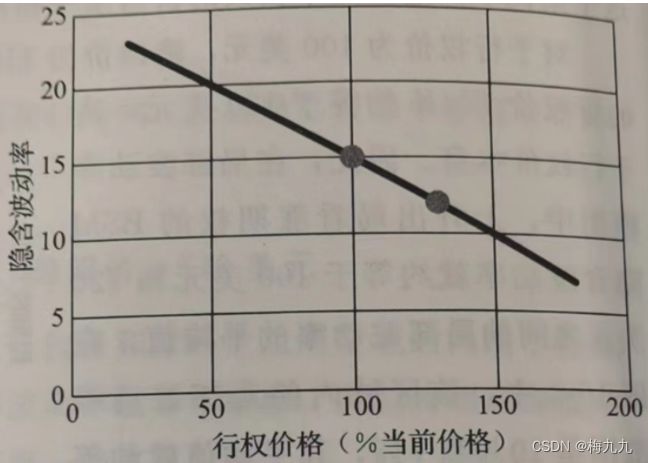
有时,用局部波动率计算的期权价值可能无法对应到任何 BSM 隐含波动率,如:当前股票价格和行权价格都是100 美元,障碍价格是130美元,斜度如下图所示。假设无风险利率等于5%:
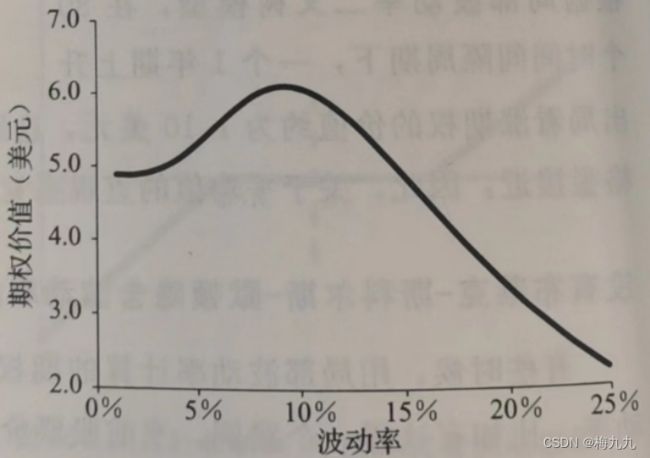
根据该斜度建立一个隐含二叉树模型,依此计算一个1年期上升出局看涨期权,在这个局部波动率模型中,得到的障碍期权价值等于6.46美元
从下图中可以看到,在没有斜度的情况下,这个上升出局看涨期权的 BSM 最大价值等于6.00美元,对应的隐含波动率等于9.5%。这个价值小于局部波动率模型得到的期权价值。没有哪个BSM隐含波动率可以对应这个局部波动率模型下的期权价值
最接近于正确期权价格的隐含波动率是 9.5%。可以这么理解:斜度可以表示为每10个行权价单位对应1个波动率单位,根据两倍定律,局部波动率的斜度就是每5个行权价单位对应1个波动率单位
一个行权价为100美元,障碍价为130美元的上升出局看涨期权可以用一个行权价为100美元的普通看涨期权和一个行权价为 B 2 / K = 169 B^2/K=169 B2/K=169 美元的映射看跌期权来复制,因此在估值中用到的就是股票价格在100美元和169美元之间的局部波动率。当斜度等于每5个行权价单位对应1个波动率单位的时候,相应的局部波动率从15%变到 1 % ≈ 15 % − ( 69 % / 5 ) 1\%\approx15\%-(69\%/5) 1%≈15%−(69%/5),在这个价格范围内的平均局部波动率就约等于8%。即就算是对奇异期权而言,隐含波动率也约等于当前股票价格和行权价格之间的局部波动率的平均值
回望看涨期权
路径依赖期权相当于内含了多个市场水平的行权价,因此对于各个区间内局部波动率都很敏感
先来看一个回望看涨期权,该期权约定在到期日所支付的是,指数的最终价值与该指数在初始日与到期日之间的最小值之间的差值。用 M t M_t Mt 表示指数在初始日与 t t t 时刻之间的最小值。假设期权在 t t t 时刻的价值为 C L B ( S t , M t , τ ) C_{LB}(S_t,M_t,\tau) CLB(St,Mt,τ),其中 τ \tau τ 表示距到期日的时间,则期权在到期日的价值就可以表示为:
C L B ( S T , M T , 0 ) = max ( S T − M T , 0 ) C_{LB}(S_T,M_T,0)=\max(S_T-M_T,0) CLB(ST,MT,0)=max(ST−MT,0)
首先证明,当最小值就是当前指数价格的时候,即 S t = M t S_t=M_t St=Mt 时,回望看涨期权的BSM delta值约等于0。当 S t = M t S_t=M_t St=Mt 时, S t S_t St 小幅上涨与 M t M_t Mt 小幅下降对期权价格的影响是相同的,于是存在
∂ C L B ∂ S ∣ S t = M t = − ∂ C L B ∂ M ∣ S t = M t \frac{\partial C_{LB}}{\partial S}|_{S_t=M_t}=-\frac{\partial C_{LB}}{\partial M}|_{S_t=M_t} ∂S∂CLB∣St=Mt=−∂M∂CLB∣St=Mt
假设指数价格在下一个时间间隔阶段发生了无限小的上行或下行, d S = S σ τ dS=S\sigma\sqrt{\tau} dS=Sστ,如下图所示,在价格上行时 M t M_t Mt 不会变化,但价格下行时 M t M_t Mt 会减少 d S dS dS
风险中性条件下,假设无风险利率等于0,根据逆向归纳法:
C L B ( S t , S t , τ ) = 1 2 C L B ( S t + d S , S t , τ + d t ) + 1 2 C L B ( S t − d S , S t − d S , τ + d t ) C_{LB}(S_t,S_t,\tau)=\frac{1}{2}C_{LB}(S_t+dS,S_t,\tau+dt)+\frac{1}{2}C_{LB}(S_t-dS,S_t-dS,\tau+dt) CLB(St,St,τ)=21CLB(St+dS,St,τ+dt)+21CLB(St−dS,St−dS,τ+dt)
对右侧运用泰勒展开可以得到:
C L B ( S t , S t , τ ) ≈ 1 2 [ C L B ( S t , S t , τ ) + ∂ C L B ∂ S d S + ∂ C L B ∂ M 0 ] + 1 2 [ C L B ( S t , S t , τ ) − ∂ C L B ∂ S d S − ∂ C L B ∂ M d S ] ≈ C L B ( S t , S t , τ ) − ∂ C L B ∂ M d S 2 → ∂ C L B ∂ M ≈ 0 C_{LB}(S_t,S_t,\tau)\approx\frac{1}{2}[C_{LB}(S_t,S_t,\tau)+\frac{\partial C_{LB}}{\partial S}dS+\frac{\partial C_{LB}}{\partial M}0]\\+\frac{1}{2}[C_{LB}(S_t,S_t,\tau)-\frac{\partial C_{LB}}{\partial S}dS-\frac{\partial C_{LB}}{\partial M}dS]\\\approx C_{LB}(S_t,S_t,\tau)-\frac{\partial C_{LB}}{\partial M}\frac{dS}{2}\\ \to\frac{\partial C_{LB}}{\partial M}\approx0 CLB(St,St,τ)≈21[CLB(St,St,τ)+∂S∂CLBdS+∂M∂CLB0]+21[CLB(St,St,τ)−∂S∂CLBdS−∂M∂CLBdS]≈CLB(St,St,τ)−∂M∂CLB2dS→∂M∂CLB≈0
于是当 S t = M t S_t=M_t St=Mt 时:
∂ C L B ∂ S ∣ S t = M t = − ∂ C L B ∂ M ∣ S t = M t ≈ 0 \frac{\partial C_{LB}}{\partial S}|_{S_t=M_t}=-\frac{\partial C_{LB}}{\partial M}|_{S_t=M_t}\approx0 ∂S∂CLB∣St=Mt=−∂M∂CLB∣St=Mt≈0
在这种情况下,回望期权的 delta 值约等于0
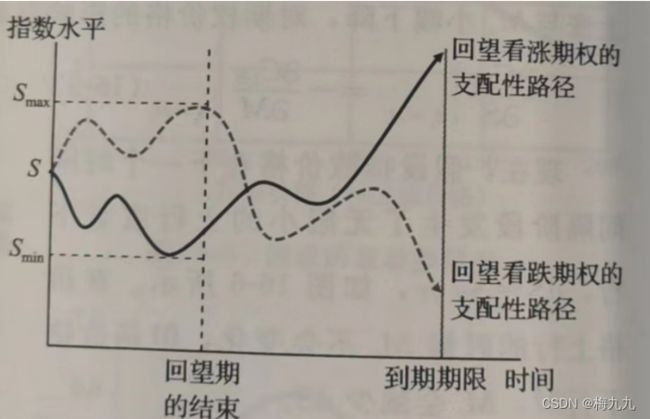
现在假设有一个1年期的回望看涨期权和看跌期权,每个期权的行权价都有3个月的回望期。看涨期权和看跌期权在到期日的损益分别为 max ( S T − S min , 0 ) , max ( S max − S T , 0 ) \max(S_T-S_{\min},0),\max(S_{\max}-S_T,0) max(ST−Smin,0),max(Smax−ST,0),其中 S m i n , S max S_{{min}},S_{\max} Smin,Smax 分别是指数在期权有效期前3个月内的最低值与最高值。。我们通过模拟指数的变动路径来对这些证券进行估值,这些路径上的局部波动率是从相应的隐含波动率微笑曲线中提取出来的。我们计算每一条路径对应的回望期权最终损益的现值,再计算所有路径现值的平均值,这就是期权的价值
上图展示了一条对于回望看涨期权和看跌期权的价值起支配性作用(该路径对期权价值的影响最大)的指数变动路径。回望看涨期权的这条支配性路径在前3个月就确定了一个较低的行权价,接着实现了较高的损益。在前3个月内确定行权价之后,这个回望期权看起来就像一个标准的欧式看涨期权。理论上,这个看涨期权的价值取决于:1、出现低行权价的可能性;2、接下来指数的波动率情况。与此相似,一个回望看跌期权的支配性路径就是最早确定高行权价,随后回落的指数变动路径。其价值也取决于:1、出现高行权价的可能性;2、接下来指数的波动率情况
在波动率斜度为负的隐含树模型中,较高的行权价和指数水平对应的是较低的指数波动率。因此,相比斜度等于0的情况,在回望看涨期权的支配性路径上, S min S_{\min} Smin 会更低一些,而随后的波动率会更高一些。与此相反,相比斜度等于0的情况,在回望看跌期权的支配性路径上, S max S_{\max} Smax 也有那么高,而随后的波动率会更低一些。因此当斜度为负的时候,回望看跌期权的价值就低于斜度为0的情况,回望看涨期权的价值会高于斜度为0的情况。如果用BSM 隐含波动率(斜度为0)来对期权进行报价,那么回望看涨期权的隐含波动率会高于回望看跌期权的隐含波动率
为了证明上述推理,假设指数当前价格水平为100,股息率等于2.5%,年化无风险利率等于6%。指数斜度为负且与到期日无关;平值期权隐含波动率等于15%,当指数行权价格每上涨10个单位,该隐含波动率会下降3个百分点。蒙特卡洛模拟结果显示,该回望看涨期权的公允价值等于指数的10.8%,而回望看跌期权的价值等于指数的5.8%。斜度为0时,回望看涨期权的BSM隐含波动率为15.6%,回望看跌期权是13.0%
下图对比了当指数价格水平为100, S min S_{\min} Smin 在一定范围内,上述回望看涨期权在隐含树模型下的delta值和BSM delta值的情况。BSM delta 值是按照 15.6% 的 BSM 隐含波动率来计算的,该隐含波动率来自有斜度局部波动率的蒙特卡罗模拟结果
可以看到,隐含树模型下求得的回望看涨期权的delta值总是小于BSM模型下,这跟我们的判断是一致的。当波动率敏感性最大(即当 S min S_{\min} Smin 接近当前指数价格水平)时,该差异也会达到最大。当 S min S_{\min} Smin 远远小于当前指数价格水平时,该差异则最小,此时回望看涨期权处于深度实值,相当于一份波动率敏感性为0的远期合约
与此相似,回望看跌期权也存在该特点,其隐含树模型下的 delta 值从数值上总是小于相应的BSM模型下的delta值