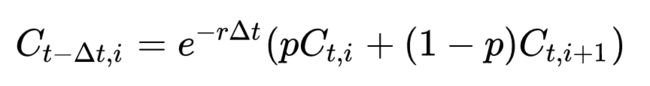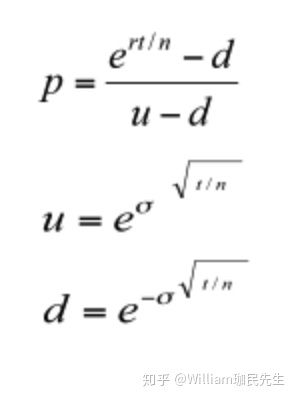python QTreeWidgetItem下面有几个子tree_【用Python金融建模】从二叉树谈起:衍生品Option期权定价模型的构建...
内容首发
乐学偶得（http://lexueoude.com) 公众号： 乐学Fintech
用代码理解分析解决金融问题
在金融里面很多地方都出现过一个理念就是“货币的时间价值”，例如我们之前聊过的利用Python对项目进行估值判断 就是利用这一重要的思想：我们做出的决定，都是把未来的一系列现金流的【流入】和【流出】进行折现，通过我们理性人在做决定的时候，是选择对我们有利的事情——也就是折现到现在NPV为正的项目去做。
那么这个世界如果真的这么简单就好了，我们只需要把未来的现金流折现到现在，然后就可以愉快的进行判断了。
可是问题来了：未来并不确定。
而且万事万物都是相互联系的，也就是说A可能导致B，B导致C，这样蝴蝶效应传递下去，一个很小的偏差或者错误的估计会导致巨大的差错。
二叉树是我们对未来进行预判的一种思考方式，也是金融里面常用的模型，二叉树的思想如下：
1.事情的发展分成一个阶段一个阶段
2.每一个阶段只有两个结果：变好和变坏
如果这是一个项目，我们可以把项目通过二叉树进行估计，最好的情况，好成什么样，最差的情况，差成什么样，一目了然：
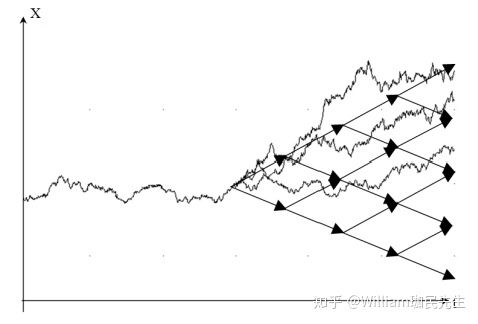
还有一个非常重要的运用就是在拟合或者模拟未来股价的趋势上，股价本质上就是一系列的时间序列，所以说与项目的估值也是一类东西：随着时间的变化，价格随之改变
我们下面就来介绍这样一个思考问题的方法与原理，并且通过Python进行建模计算：
二叉树的思想就是把未来时间轴分为一期一期，在每一期内，只有价格只有两种变化方向，向上，或者向下。我们从一期二叉树开始思考：
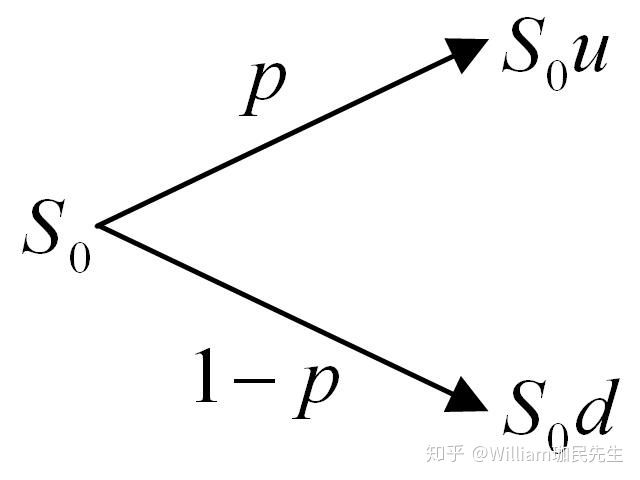
假设初始价格为S0，在第一期的时间内，有P的概率价格会上升，成为S0*u 的价格，因为在这段时间内只有两种可能，所以剩下
的1-P的概率价格会下跌，成为S0*d的价格。
u与d分别为up factor（上涨因子）与down factor（下跌因子），（我明白，涉及到公式经常会加什么什么因子，导致这个名字很山寨，但是因为多期二叉树中会用到，两个因子造成的影响也可能不一样，所以我们暂且尽量用一般公式与常见叫法去表示）
另外，我们为了多期二叉树能够重合，也就是上涨下跌与下跌上涨的结果一样，我们将u与d两个因子设立一个约束条件u*d=1
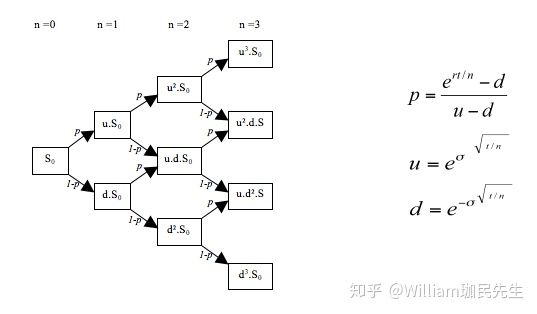
这样，我们从一期推广到多期，就可以得到如下流程图：
也就是说，我们只要能知道p（上涨概率）与u（上涨因子），就能求出1-p（下跌概率），与d（因为约束关系），这样整个未来的价格的路径就能够知道了。
好了，这样我们就知道最简单的标的资产，通过二叉树的方法进行预测未来变动，是什么样的路径了。
我们接下来再把问题弄复杂一点，假设我们研究的不是简单的标的资产，比如说并不是一个单一的项目（可以看做一系列的未来现金流）或者是一个简单的股票，而是衍生品，也就是说定价是衍生在原标的资产上的产品，那我们如何进行定价呢？
这就涉及到了二叉树运用非常多的一个方面——衍生品定价。
我们接下来还是以例子，只不过我们研究的不仅仅是标的资产（比如说股票stock），而是衍生在标的资产上的金融产品（比如说期权option）,我们该如何定价呢？
对于Call Option（看涨期权），其实价格非常好计算，X为执行价格，就是max（X-S0u^1,0）或者是max（X-S0d^1,0）,也就是说要么为执行价格与股价的差价，要么为0.
这样，我们在0时刻的期权价格也非常好计算了，
期权价格= [ p ×上涨时期权价格 + (1−p) ×下跌时期权价格] × 折现因子
当然折现因子在这里可以用连续复利也可以用离散复利的方法折现，比较推荐连续复利，因为更加准确。
那么我们到这里已经完全具备了建模的理论基础了，我们接下来用Python建立二叉树模型进行定价计算,这样不仅能巩固我们的概念，也能锻炼我们的建模能力：
我们首先可以先调整numpy的显示，因为如果期数较多的情况下jupyter notebook中会截断大量数据，我们想让数据全部显示出来：
import 然后我们只需要numpy帮我们储存一下数据并且计算即可，当然也可以用pandas，但是因为数据结构并不复杂，有点大材小用，我们用array就能搞定了。
import numpy as np我们现在可以自定义一个函数，把可以在市场上观测到的信息作为参数：
def binomial_tree_call_option_pricing_model(N,T,S0,sigma,r,K,show_array=False):
dt=T/N
u=np.exp(sigma*np.sqrt(dt))
d=1/u
p=(np.exp(r*dt)-d)/(u-d)其中N为期数，T为总时间，S0为初始价格，sigma为波动率，r为无风险利率，K为执行价格，show_array为一个开关，我们可以用show_array 来控制，是否显示array。
dt为将总时间通过除以期数切分为每一个小段，每一个小段为一期二叉树。
u为上涨多少，这个是根据上述讲到的公式来确定的，同样，为了二叉树能重合，d=1/u,通过约束关系也能表示出来。
p为上涨概率，同样根据上述讲到的公式来确定的
接着我们需要创建一个容器去储存我们的数据，我可以用numpy的zero生成全部是zero的矩阵用作存放数据的容器：
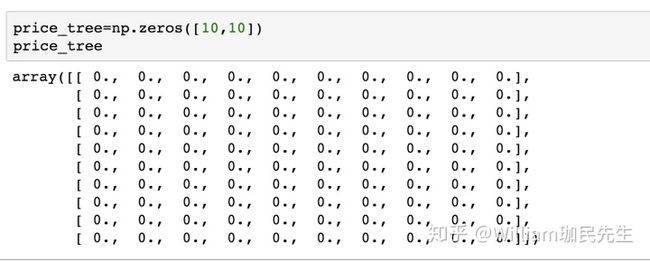
但是因为这个容器是需要随着数据的多少而随之变化，也就是不能是固定的大小，于是我们可以通过变量进行解决：
price_tree=np.zeros([N+1,N+1])然后我们就可以将这个容器里面的数据填满了，我们首先填入的是价格，也就是比如标的资产是股票的话，股票在未来T时间段里的每一个dt期间变动的可能价格，我们全部放入：
for i in range(N+1):
for j in range(i+1):
price_tree[j,i]=S0*(d**j)*(u**(i-j))这里有一个nested for loop的技巧，我们在很多list of lists， array等里面都会用到。另外，价格上升也下降我们通过N+1和i+1确定range，i和j的约束关系控制上涨个下跌的次数
接着我们依葫芦画瓢的方法先建立起option价格的tree：
我们首先计算每一个期权价格：
option_tree=np.zeros([N+1,N+1])
option_tree[:,N]=np.maximum(np.zeros(N+1),price_tree[:,N]-K)然后我们把期权价格通过反向进行折现，求出t=0时刻的价格：
for i in np.arange(N-1,-1,-1):
for j in np.arange(0,i+1):
option_tree[j,i]=np.exp(-r*dt)*(p*option_tree[j,i+1]+(1-p)*option_tree[j+1,i+1])
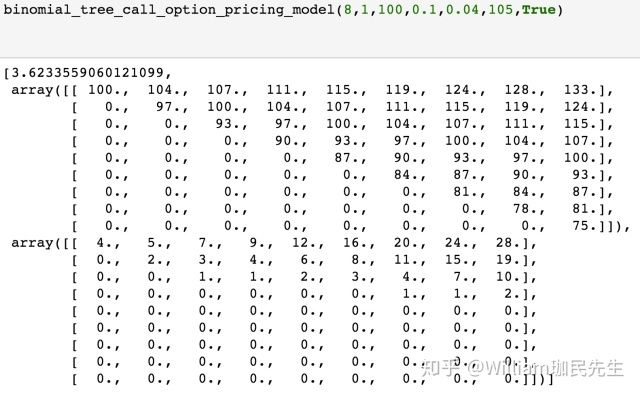
然后我们就可以直接返回array的值就可以了，因为我们在参数中直接将show_array设置成了False，所以是默认不显示出整个树状结构的：
if show_array:
return [option_tree[0,0],np.round(price_tree),np.round(option_tree)]
else:
return option_tree[0,0]这样我们能直接返回这个期权定价的初始价值，如果我们将show_array调成True，则执行第一段，将整个树状结构也就是每一个标的资产价值显示出，当然，我们为了美观，将array中的结果进行了round，没有保留小数。
当然，我们还没有讨论一个问题，就是上涨概率和下跌概率与风险中性定价原则，我们在接下来为大家介绍......未完待续......
以上为《Python零基础入门编程的新世界》部分内容笔记。用Python做爬虫，数据分析，全栈建设，Fintech金融量化，机器学习，办公自动化，树莓派，美好生活DIY，......2000+连载，不仅有编程，还有更多原理讲解。
零基础Python入门编程全栈量化AI - 网易云课堂study.163.com另外，也欢迎关注一个非常干的干货公众号： 乐学Fintech 用代码理解分析解决金融问题
