20230822 | 二叉树 Part1

定义部分来自<<代码随想录>>

二叉树的种类

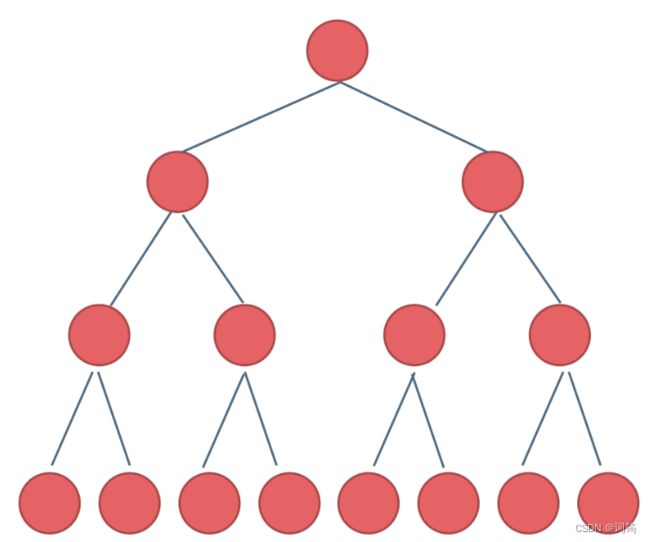
满二叉树

Definition: 二叉树只有度为0的结点和度为2的结点 + 度为0的结点在同一层上
该二叉树深度为k, 有2^k-1个结点

完全二叉树

Definition: 除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置
一层包含 1~ 2^(n-1) 个节点

Notice: PriorityQueue就是一个堆, 堆就是一个完全二叉树, 同时保证父子结点的顺序关系

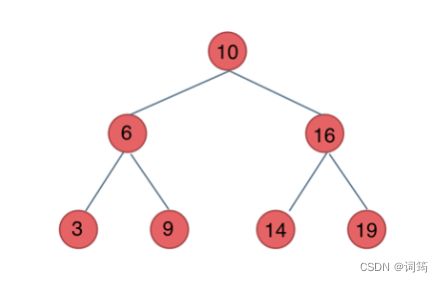
二叉搜索树

Definition:

• 若左子树不空，则左子树上所有结点的值均小于根结点的值；
• 若右子树不空，则右子树上所有结点的值均大于根结点的值；
• 左、右子树也分别为二叉排序树

插入操作：在平均情况下，插入一个元素的时间复杂度是 O(log n)，其中 n 是树中节点的数量。但在最坏情况下，如果树不平衡，插入操作的时间复杂度可能变为 O(n)。
删除操作：删除一个元素的时间复杂度与插入相似，平均情况下是 O(log n)，最坏情况下是 O(n)

平衡二叉搜索树 (AVL Adelson-Velsky and Landis)

Definition: 是一棵空树或左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

插入操作：由于这些树保持了平衡性质，插入操作的平均和最坏时间复杂度都是 O(log n)。插入后需要进行平衡调整。
删除操作：删除操作的平均和最坏时间复杂度也是 O(log n)，因为平衡树的结构会在删除后自动调整以保持平衡。

二叉树的存储方式

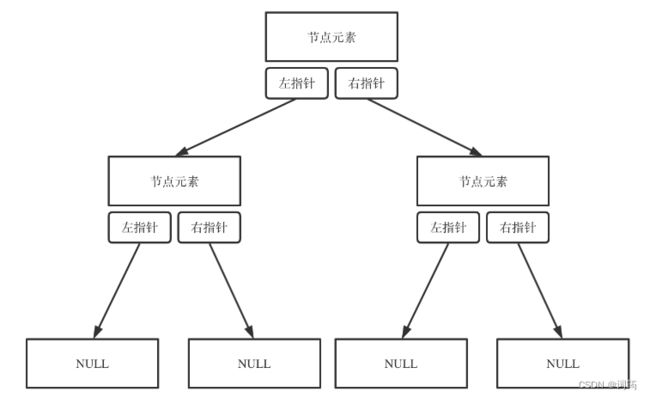
链式存储 -> 指针

通过指针把分布在各个地址的节点串联一起

顺序存储 -> 数组

存储的元素在内存是连续分布

如果父节点的数组下标是 i，那么左孩子就是 2i+1，右孩子就是 2i+2。

二叉树的遍历方式

DFS

先往深走, 遇到叶子节点再往回走
eg. 前/中/后序遍历 (递归 迭代)

BFS

一层一层的去遍历
eg. 层次遍历 (迭代)

栈与队列

• 栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
• 广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

二叉树的定义

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

递归

Notice: 每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

三要素:

1. 确定递归函数的参数和返回值
2. 确定终止条件: 以免发生栈溢出
3. 确定单层递归逻辑: 重复调用自己来实现递归过程

Leetcode144 前序遍历

Method1: 遍历二叉树

class Solution {
    LinkedList list  = new LinkedList<>();
    public List preorderTraversal(TreeNode root) {
        traverse(root);
        return list;
    }
    public void traverse(TreeNode root){
        if (root == null) return;
        list.add(root.val);
        traverse(root.left);
        traverse(root.right);
    }
}

Method2: 分解问题

前序遍历 = root + left前序遍历 + right前序遍历

class Solution {
    public List preorderTraversal(TreeNode root) {
        LinkedList list = new LinkedList<>();
        if (root == null) return list;
        list.add(root.val);
        list.addAll(preorderTraversal(root.left));
        list.addAll(preorderTraversal(root.right));
        return list;
    }
}

二叉树的迭代遍历

前序遍历

前序遍历顺序：中-左-右，入栈顺序：中-右-左

class Solution {
    public List preorderTraversal(TreeNode root) {
        ArrayList result = new ArrayList<>();
        if (root == null) return result;

        Stack stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            while (node.right != null){
                stack.push(node.right);
            }
            while (node.left != null){
                stack.push(node.left);
            }
        }

        return result;

    }
}

中序遍历

中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再把节点的数值放进result数组，这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

中序遍历顺序: 左-中-右 入栈顺序： 左-右

class Solution {
    public List inorderTraversal(TreeNode root) {
        List result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
}

后序遍历

class Solution {
    public List postorderTraversal(TreeNode root) {
        List result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}