前端算法之复杂度
- 算法
- 算法概述
- 复杂度
- 时间复杂度
- 时间复杂度总结
- 多维复杂度
- 时间复杂度细分
- 时间复杂度举例
- O1常数时间复杂度:
- Olog n对数时间复杂度:
- On线性时间复杂度:
- On log n线性对数时间复杂度:
- On^2平方时间复杂度:
- On^3立方时间复杂度:
- 空间复杂度
- 时间复杂度总结
- 时间复杂度
算法
算法概述
- 复杂度
- 双指针
- 滑动窗口
- 二叉树
复杂度
更短的时间,更少空间
O(n) 算法执行的所有时 规模
时间复杂度
时间复杂度是计算机科学中的一个概念,用于衡量 一个算法执行时间随输入规模变化的程度。
对于同一个算法,运行时间随着输入数据量的增加而呈线性增长,那么它的时间复杂度就是 O(n),这里的n代表输入数据量。
例如,
-
插入排序的时间复杂度是O(n^2),因为对于n个元素的列表,它需要进行n*(n-1)/2次比较和交换。
-
快速排序的时间复杂度则是O(nlogn),因为它在平均情况下只需要对列表进行一次分割,然后对两个子列表分别进行排序,最后再进行一次合并。
时间复杂度可以用来评估算法的效率,特别是在处理大规模数据时。
在设计和选择算法时,应尽量选择时间复杂度较低的算法,以提高程序的运行效率。
function a(){
console.log('hello')
return 1
} // 总共执行 2次
function b(){
for(let i = 0 ; i < n ;i++){ // n+1 次
console.log('hello') // n 次
}
return 1 // 1 次
} // 总共执行 2n+2次
function c(){
let sum = 0; // 1 次
let i = 1; // 1 次
let j = 1; // 1 次
for( ; i < n ;i++){ // n 次
j = 1 // 1 * n 次
for( ; j < n ;j++){ // n * n 次
sum = sum + i + j // n * n 次
}
}
} // 总共执行 2 (n^2) + 2n + 3 次
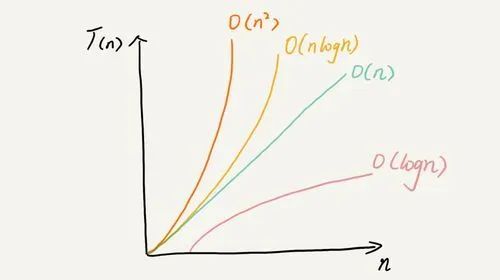
时间复杂度总结
- 时间复杂度 量级最大的部分,影响最大
- 循环、嵌套、递归 有多维复杂度概念
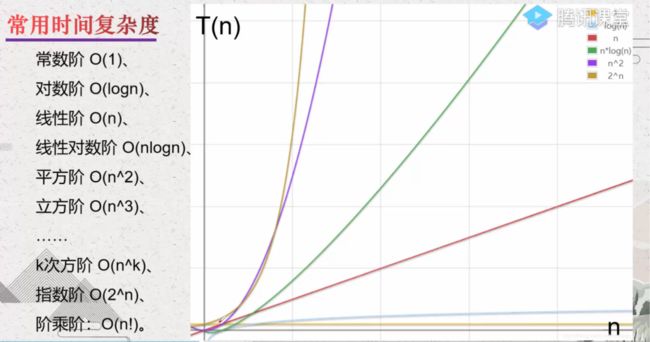
O(1) --> O(logN) --> O(N) --> O(NlogN) --> O(N^2)–> O(N^3)
// 二分查找算法 -- O(logN)
let i = 1
while(i <= n ){
i = i * 2
}
// log2^n 可称为 logN
// ----------------------//
function a (n){
let i = 1
while(i <= n ){
i = i * 2
}
return i
}
function cal(n){
let sum = 0
for(let i = 0 ; i < n ;i++){
sum ++ a(n)
}
return sum
}
多维复杂度
多维复杂度通常指的是多个维度上的复杂度,它用于衡量一个系统或模型在多个维度上的复杂程度。
在计算机科学和人工智能领域中,多维复杂度通常用于评估算法的效率、计算时间、空间需求等。
它可以帮助我们更好地了解算法的复杂性和性能,以便进行优化和改进。
多维复杂度可以包括时间复杂度、空间复杂度、算法复杂度等。
其中,时间复杂度指的是算法执行时间的复杂性,空间复杂度指的是算法所需存储空间的大小,算法复杂度则指的是算法本身的复杂性。
在计算多维复杂度时,需要考虑算法在不同维度上的性能表现,以便更好地评估其效率和可行性。
这有助于我们在设计和实现算法时做出更好的决策,并提高算法的效率和性能。
时间复杂度细分
- 最好情况下的时问复杂度
- 最坏情况下的时问复杂度
- 平均情况下的时问复杂度
- 均摊时问复杂度
举例
- 12345 O(1)
- 3n+4 O(n)
- 3n^2 + 4n + 5 O(n^2)
- 3log2^n + 4 logn
- 2^n O(2^n)
时间复杂度举例
以下是一些时间复杂度举例说明:
O(1)常数时间复杂度:
比如在数组中查找一个元素,无论数组的大小如何,查找操作的时间始终是一个常数,这就是O(1)的时间复杂度。
类似的操作还有 访问数组中的某个元素、插入或删除链表中的某个节点等。
O(log n)对数时间复杂度:
比如二分查找算法,每次比较都可以将搜索范围缩小一半,因此其时间复杂度为O(log n)。
O(n)线性时间复杂度:
比如 遍历一个数组或列表的所有元素,时间与数组或列表的大小n成正比,其时间复杂度为O(n)。
类似的算法还有线性查找、简单排序等。
O(n log n)线性对数时间复杂度:
比如 快速排序 和 归并排序 等算法的时间复杂度是O(n log n)。
这些算法在处理大规模数据时效率较高。
O(n^2)平方时间复杂度:
比如 冒泡排序 和 插入排序 等算法的时间复杂度是O(n^2)。
这些算法在处理小规模数据时效率较高,但在处理大规模数据时可能会较慢。
O(n^3)立方时间复杂度:
比如矩阵乘法等操作的时间复杂度是O(n^3)。
这种时间复杂度通常在处理大规模数据时效率较低。
这些时间复杂度可以用来评估不同算法的效率,根据实际问题的规模和特点选择合适的算法。
更多详细内容,请微信搜索“前端爱好者“, 戳我 查看 。
空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。它也是 问题规模n的函数。
算法的空间复杂度一般以数量级的形式给出。
在评估一个算法时,除了时间复杂度外,空间复杂度也是一个重要的考虑因素。
一个高效的算法应该具有 较好的时间复杂度和较小的空间复杂度。
空间复杂度的分析可以帮助我们了解算法在运行过程中所需的最大存储空间,从而为算法的实现和优化提供指导。
在算法设计和分析时,应尽可能减少算法的空间复杂度,以避免过多的内存占用和资源浪费。
需要注意的是,空间复杂度只考虑算法运行过程中临时占用的存储空间,并不包括算法本身所占用的存储空间。
如果需要全面评估算法的效率,还需要考虑算法的时间复杂度和其他性能指标。
inction a(n) {
const arr = [];
arr.length = n; // 开辟了空间
for(let i = 0; i < n; i++) {
arr[i] = i *i
}
}
趋势: O(1) --> O(logN) --> O(N) --> O(NlogN) --> O(N^2)–> O(N^3)