CSU计算机学院2021年C语言期末题目思路分享（后两道题）

E: 实数相加——大数加法的拓展

原题

题目描述

C语言就要期末考试了，经过一学期的学习，小南学会了分数相加、分数相减、大整数相加，可就是没有尝试过将两个最大达400位的实数相加。在调试过程中，小南遇到了很多问题，一直解决不了。你能帮他编写一个程序实现两个实数相加吗？

输入

多组样例。每行输入一个样例包括两个用空格分开的实数_x_和_y_，其中_x_和_y_是长度不大于400位的非负实数。注意，非负实数中也可能包括非负整数，正整数会省略小数点和后面的0，只包括整数部分。

输出

对于每一行输入，输出两个实数_x_和_y_相加的结果。输出结果中整数部分的前面和小数部分的末尾不输出多余的0；如果是整数，不输出小数点和小数点后面的0。每个输出占一行。

样例输入

1.1 2.9
1.1111111111 2.3444323343 
1 1.1
1.1111 1.1889

样例输出

4
3.4555434454 
2.1
2.3

题目思路

给出的数据明显超过任何一个数据类型，属于大数处理的类型，具体可以b站搜索大数加法、大数阶乘先进行学习，基础的大数加法需要熟练，这样遇到这样的类似的进阶题，思路会更清晰。考过了大数加法，大数阶乘会不会考呢？是有可能的，大数阶乘也是大数加法的拓展。

这题是“实数”的大数处理，也就是有可能有小数点了。我一开始想的是先把小数点去掉，然后按大整数的加法来，原来大整数是右对齐进行计算，现在改为“居中对齐”计算，也就是小数点的位置对齐，然后从右往左计算，想法有，但是很难实现，单是这个“对齐”，已经非常麻烦了。

换个思路，毛主席教导我们：“事物都是一分为二的。”，这一串字符串也不是铁板一块，必然也能一分为二，分成“整数”和“小数”两部分，对这两部分分别使用大数加法。其中，整数部分就是最常见的倒序加法。小数部分就是左对齐的大数加法。

下面我们就看一下实现的步骤，从中能看到很多需要注意的地方，和我犯错误的一些经验教训。

实现步骤

读入的是一整串数据，首先需要分成整数和小数部分，分界点就是小数点。这里用for循环是可以解决的。

这两部分数据使用char数组存储。在存储整数的char数组内，我们要使用字符的数字进行存储，而非把原始数据减去'0'，但是小数部分却可以把原始数据减去'0'进行存储。为什么呢？这就需要先了解大数是怎么存储的。

大数是怎么存储的呢？大数加法一般用的是char数组存储每一个数字。整个数组的长度是大于输入的数字的长度的，也就是说，输入的数字，或者是计算后的数字，一般是填不满数组的，那么，剩下的空位置怎么办，怎么样能不影响计算和数组长度的判断，就需要思考。惯例是使用空字符填充，并且，读入的原始数据，是'0'、'1'，这样的字符，一般为了方便计算和初始化，会在存储的时候减去'0'。这样，字符串首先是计算方便了许多——直接用数组成员相加就行了，不用担心忘记减'0'，其次，这样不影响计算——0加0还是零。

要回答最开始的问题——整数和小数为何要区别对待，这样说还是不够的。我们还需要了解整数和小数相加方式的不同。

整数的相加是常见的题型，具体可以去看b站的视频。由于整数的加法是从个位开始的，也就是右对齐的（想象列竖式的场景），所以需要一种办法，对齐个位数。这里有两条路，一个是右对齐，然后从右加到左，我在期中考试的时候就是这样写的，那时候没有看其他的文章视频，按最直观的办法想到的，而且那个题并不要求计算结果，只要统计进位次数。其实大数处理最好的办法是另一个办法，就是倒序存储后从左往右做加法，然后从右往左读取结果。这里重点说这个倒序的办法。

而小数的相加，明显是左对齐的，但也是从右往左相加。此时为何区别对待小数和整数的原因已经可以窥见一二，整数由于其右对齐的特性，需要倒序，小数因为是左对齐加法的，而数组存储本来就是左对齐的，就不需要倒序。问题就出在这个倒序上。

我们来看看，如果把整数部分用数字，也就是0, 1, 2 ,3这样的数字（不是'0'、'1'、'2'、'3'这样的字符，这四个字符在ASCII中代表48，49，50，51四个数字）然后进行反向，进行相加，会怎么样：我们会发现无法分别出整数末尾的0和本来数组中用来占位的0！这并不奇怪，因为这两个0是一样的，在ASCII码中都代表空字符。我就在这里错了一次。

那么，我们还能把整数的字符转成数字吗，答案是肯定的，但是需要在反转的时候同步进行转换。

void reverse(char buffer[], char a[])
{
    for (int tmp = 0, i = strlen(buffer) - 1; i >= 0; i--) {
        a[tmp++] = buffer[i] - '0';  // 边倒序，边变化形式
    }
}

这样做为什么就没关系了呢，其实，关键在反转时候的strlen上，之前那样的做法，不仅是混淆了两种0的，更是无法确定数组的长度——长度是靠第一个出现的空字符确定的，只要在反转之前，我们可以区分这两个0，也就是使用'0'、'1'、'2'、'3'这样的字符进行存储，我们就能正确读出字符串的长度，此时进行反转，就会在正确的字符串长度的范围内反转。

很抽象，来看看图，假设要计算1300+1400，如果全部用数字存储，就会变成这样：

反转数组的时候，程序使用的strlen也会把长度算成2而不是4：

使用正确的办法：

反转后：

这里把0放在了前面，虽然strlen依然不准，但没有人让我们用strlen了！之后我们只需要从最右边往左相加，然后结果中，从右往左遍历，找到第一个不为0的数开始输出即可。最后的代码中可以看到这个过程。

其实这已经把整个题的思路说完了。剩下的细枝末节，其实只要把核心思路掌握，就是一些对核心思路的运用，比如小数相加中，结果中结尾有很多0，怎么去除？整数的思路是从右往左，从第一个不为0的数开始输出，明显小数不能这样——小数没有倒序呢。但是可以运用相同的思路，从右往左，找到第一个不为0的数，记下它的数组下标，然后输出的时候，只要从头输出到这个位置即可。

还要注意题目中的许多细节，比如也有整数加整数、整数加小数的情况出现，此时要判断是否有小数点。还要判断小数部分全为0的时候，此时不输出小数点和小数部分，诸如此类就不再赘述，可以参看代码和注释。

代码和注释

代码中包含详细的注释，命名也尽量明确意思。
题外话，在此提几个倡议：

1. 稍复杂的程序中尽量用一些单词和下划线命名，用一些拼音也行，尽量不要abcd ijk mnopq到底，比较容易混淆
2. 多用空格！等号、加号、减号两边、逗号右边、中括号之后等地方加上空格，会让代码舒服非常非常多
   当然这是细枝末节的问题，代码风格取决于个人。

#include 
#include 

#define MAX_LEN 410

void reverse(const char buffer[], char a[]) // 把前一个数组反向后存储到后一个数组中，因为对前一个数组只读，加一个const
{
    for (int tmp = 0, i = strlen(buffer) - 1; i >= 0; i--) {
        a[tmp++] = buffer[i] - '0';
    }
}

int main()
{
    char a[MAX_LEN] = {0}, b[MAX_LEN] = {0};
    while (~scanf("%s %s", a, b)) {
        int alen = strlen(a), blen = strlen(b), adot = alen, bdot = blen, up = 0;                        // 给adot赋值的值是，如果没有小数点，adot的默认值，在这个值下，两个存储小数的循环不会执行，这样小数的数组就全是0，不会影响计算
        char a_float[MAX_LEN] = {0}, b_float[MAX_LEN] = {0}, a_int[MAX_LEN] = {0}, b_int[MAX_LEN] = {0}, // 这是用来分别存储整数小数部分的，都是正序
            float_result[MAX_LEN] = {0}, int_result_reverse[MAX_LEN] = {0},                              // 这是用来存储算术结果的，小数是左对齐计算，整数是右对齐计算，因此一个是正序，一个是倒序（右对齐计算采取了倒序再相加的策略，因此结果也是倒序）
            a_int_r[MAX_LEN] = {0}, b_int_r[MAX_LEN] = {0};                                              // 这是整数部分的倒序，用于上述的倒序计算
        int is_adot = 0, is_bdot = 0;                                                                    // 是否具有小数点，用于最后判断要不要输出小数点和小数部分（两者都没有小数部分，即不输出小数点和小数部分）
        // 两个for循环，分别记录小数点的位置，以一分为二
        for (int i = 0; i < alen; i++) {
            if (a[i] == '.') {
                adot = i;
                is_adot = 1;
                break;
            }
        }
        for (int i = 0; i < blen; i++) {
            if (b[i] == '.') {
                bdot = i;
                is_bdot = 1;
                break;
            }
        }
        // 四个for循环，分别存储a、b数的整数、小数部分
        for (int i = adot + 1; i < alen; i++) {
            a_float[i - adot - 1] = a[i] - '0'; // 小数可以减去'0'存储
        }
        for (int i = bdot + 1; i < blen; i++) {
            b_float[i - bdot - 1] = b[i] - '0';
        }
        for (int i = 0; i < adot; i++) {
            a_int[i] = a[i]; // 整数在反转的时候在减去'0'存储
        }
        for (int i = 0; i < bdot; i++) {
            b_int[i] = b[i];
        }

        // 因为小数是左对齐相加，因此直接从右往左做大数加法计算即可
        for (int i = MAX_LEN - 1, tmp; i >= 0; i--) {
            tmp = a_float[i] + b_float[i] + up;
            up = tmp / 10; // 进位，用这种形式可以不用if语句判断tmp是否大于等于10，更加简洁明了
            float_result[i] = tmp % 10;
        }

        // 因为整数是右对齐相加，因此需要将两个加数倒序后，从左往右对倒序后的数列做大数加法计算
        reverse(a_int, a_int_r);
        reverse(b_int, b_int_r);
        for (int i = 0, up1 = 0, tmp; i < MAX_LEN; i++) {
            tmp = a_int_r[i] + b_int_r[i] + up + up1;
            up = 0;
            up1 = tmp / 10;
            int_result_reverse[i] = tmp % 10;
        }

        // 倒序标记小数，标出从右到左第一个不为0的值，后续从左往右输出到这个位置即可
        int float_not_zero_index = 0, is_empty = 1; // is_empty判断小数部分是否为空，以决定要不要输出小数点和小数部分
        for (int i = MAX_LEN - 1; i >= 0; i--) {
            if (float_result[i] != 0) {
                float_not_zero_index = i;
                is_empty = 0; // 但凡执行到这里，就说明小数部分不为空，不执行到这里，is_empty默认是1，也就是为空
                break;
            }
        }

        // 倒序输出整数结果，从右往左，从第一个不为0的数开始输出
        int is_int_empty = 1; // 判断整数部分是否为空，如果为空需要手动输出一个0，原理和上面那个控制变量一样
        for (int i = MAX_LEN - 1; i >= 0; i--) {
            if (int_result_reverse[i] != 0) {
                for (i; i >= 0; i--) {
                    printf("%d", int_result_reverse[i]);
                    is_int_empty = 0;
                }
            }
        }
        if (is_int_empty) { // 如果整数部分为空，手动输出一个0
            printf("0");
        }

        // 任意一个数有小数点，并且小数部分不为空，输出就要有小数点和小数部分
        if ((is_adot || is_bdot) && !is_empty) {
            printf(".");
            for (int i = 0; i <= float_not_zero_index; i++) {
                printf("%d", float_result[i]);
            }
        }
        // 统一输出换行符
        printf("\n");
    }
}

F: 谍影寻踪——链表的思想和运用

原题

题目描述

2020年10月，国家安全机关组织实施“迅雷-2020”专项行动，破获数百起间谍窃密事件，有效维护了国家安全和利益。在行动中，我方安全机关破获了一个情报组织，他们是单线联系的。我方给情报组织中的每个人员一个唯一的代号。同时，情报人员为了隐秘，可能会有不同的姓名编号（设定最多两个姓名编号）。我方顺藤摸瓜，分别截获并返回组织信息。请你帮忙汇总并恢复这条组织链条。

输入

多组样例。每组样例包括多行输入，第一行包含一个正整数_n_（0<n_≤1000），表示截获到的情报数。接下来的_n_行输入形式为A->B，表示A单向联系B，B是A的下线。A和B表示两名组织人员的信息，包括代号_x_和姓名编号_y，用逗号“,”分开。代号_x_和姓名编号_y_为整数，满足1≤_x_,_y_≤999999。除了第一行，A或B的代号信息在之前的行中出现过。

输出

对于每一组样例，按照顺序在一行中输出该组织的所有成员的信息，用“->”间隔。每个输出占一行。如果有一个代号有两个姓名编号，则认为是一个成员，输出代号和对应的两个姓名编号，用“#”分开。如有两个信息1,2345和1,6666，输出时对应一个成员信息1,2345#6666，两个姓名编号先输入的在前面。

样例输入

3
1,1234->5,2236
5,2236->3,7177 
7,3234->1,1234
4
1,258->10,111111
5,4353->1,36900 
7,22->5,4353
10,159->20,220102
2
1,111->2,222
1,101->2,202

样例输出

7,3234->1,1234->5,2236->3,7177 
7,22->5,4353->1,258#36900->10,111111#159->20,220102
1,111#101->2,222#202

题目思路

看到这个题目名字第一时间想到电影谍影重重和碟中谍，还是很喜欢这类片子的。

题目明显是考察链表的运用，这部分知识需要先掌握，可以看各种书，完成一些书后的习题，上b站搜一些视频学习一下，差不多就可以了。

起初没有看到题目中的“除了第一行，A或B的代号信息在之前的行中出现过”，思来想去了很久AB两者都是第一次出现的情况，还好没想出来具体的实现方法，不然写代码的时间恐怕要翻倍了。

我们还是按实现步骤梳理一下。

既然每一次的代号信息都在之前出现过，那么每一行输入就是对链表的增添。那么自然最开始的时候要有一个初始的链表，要有链表，就先要有个结构体，于是在代码开头，我们写一个结构体。

要包含什么数据呢？题目很明确：名字，代号，可能存在的第二代号。仔细一想，我怎么知道有没有第二代号呢？于是加一个新的标识符is_code2，等于1就是有第二代号，等于0就是没有。

顺便说一下，用is开头命名控制变量有个好处，在判断的时候很明确，比如 if (is_code2) ，即可，英文意思很清楚，“如果是有第二代号”嘛。

结构体就是这样，next作为指针指向下一个结构体，构成链表：

struct spy {
    int name, code1, code2, is_code2;
    struct person *next;
};

结构体有了，说好了要建一个链表的。具体来说就是用第一行的信息组建一个链表，我们用代码来解释：

        struct spy *head;
        
        head = malloc(sizeof(struct spy));
        head->next = malloc(sizeof(struct spy));
        scanf("%d,%d->%d,%d", &head->name, &head->code1, &head->next->name, &head->next->code1); // 第一次扫，先建立一个初始的链表
        head->is_code2 = head->next->is_code2 = 0;                                               // 都还没有第二代号，标识符为假
        head->next->next = NULL;

开始需要malloc一些内存，因为第一行代码只是建立一个指针，指向哪里还不知道，分配完内存后，本质是一种质变，本来无意义的内存变成了“结构体”性质的内存，所以分配完内存后，就可以把head看作指向一个结构体的指针了。

什么时候不需要malloc呢？知道了原理其实不言而喻了，假设已经有一个指针p指向了某个结构体，此时写struct spy *head = p;，自然是把head也指向那个结构体，显然就不需要再用malloc了。提一句，这个声明变量要看作两部分struct spy *和head，表示声明一个变量head，这个变量的类型是“指向某个spy类结构体（具体哪个还不知道，这里的指向只是它的形式，而非内容）的指针”，不要看成struct spy 和*head，后者容易引起疑惑。

由于输入的第一行给出两个人的信息，所以初始链表也要包含两个人，其形式就是下面这样的：

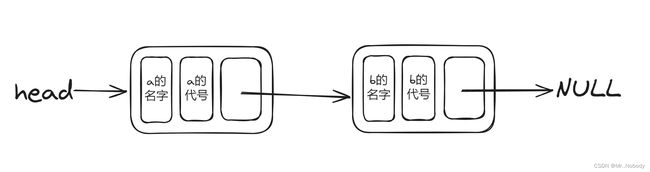
接下来的任务就是找和插入了——找到后续输入的a（或b），在a的后面（或b的前面）插入一个新的链表即可 。我采用的是单个指针，使用p和p->next两步判断——p判断是不是a，p->next判断是不是b，最终的结果，都是在p的后面增加指针。这引出了许许多多的问题，修修补补了很多地方才正确，肯定是有大佬有优雅得多的办法的。我就浅谈一下我的思路。可以对照后文的代码看。

首先scanf一些数据，我们把第一行之后的每行数据存入临时的变量a_name a_code b_name b_code中，即我们称前一个人为a，后一个为b，接着我们开始遍历链表。

p从左往右移动，每次做两个判断：p指向的人的name（即p->name）等于输入的a_name吗？p->next的name（即p->next->name）等于输入的b_name吗？如果其中一个判断为真，就创建一个新的spy结构体，插入其中（插入的具体过程可以参看b站视频和后文代码，如果p是a，就在p后插入b；如果p->next是b，就在p后插入a），一旦插入成功，就break退出遍历，防止重复修改链表。遍历的过程大概如图所示：

而题目还要求一个第二代号，这就让问题更加复杂，我的想法是在每次对name的判断为真后，接着判断这个位置是否具有第二代号，如果有就写入代号信息。（具体参看后文代码）

这看似很好，其实还是有很多纰漏，即需要考虑到一些特例：

1. 如果第一次p的位置是b怎么办？此时p判断的是a，察觉不到它和b相等，而即使p往右移动，也不会有判断head这个位置是不是b_name的过程。
2. 如果遇到了两个判断同时为真怎么办？此时虽然会正确地插入，但是如果此时出现了第二代号的问题，就得不到正确结果（也就是第四个输入样例的情况，说实话，要是没有这个输入样例，我用我的这种办法自己可能很难想到这种情况）
3. 如果p指向的是最后一个结构体，那么p->next就指向的是NULL空指针，此时访问p->next->name就会出错，怎么避免？

第一个问题，这就需要加一个判断，来判断head指针指向的结构体是否是b，如果是的话，就在链表头部插入a。

第二个问题比较抽象了，就要在判断p为a后，在判断是否有第二代号的时候加入一个判断——即加入p->next->name和b是否相等，且code是否不一样，如果不一样就要写入b的第二代号。

第三个问题比较明确，需要在if语句中使用p->next != NULL && p->next->name == b_name，由于有短路机制的存在，前者判断为假（即指向空指针），就不会判断后者，自然就不会访问p->next->name了

核心思想就是这么多。具体还是来看代码和注释吧：

#include 
#include 
#include 

struct spy {
    int name, code1, code2, is_code2;
    struct spy *next;
};

int main()
{
    int n;
    while (~scanf("%d", &n)) {
        struct spy *head; // 头指针，它将要指向第一个结构体

        head = malloc(sizeof(struct spy));                                                       // 分配结构体空间，此时head成为**具体的**指向这个结构体的指针了
        head->next = malloc(sizeof(struct spy));                                                 // 分配下一个结构体空间（也就是输入中的第二个人）
        scanf("%d,%d->%d,%d", &head->name, &head->code1, &head->next->name, &head->next->code1); // 第一次读入，先往初始链表中的结构体中写入信息
        head->is_code2 = head->next->is_code2 = 0;                                               // 因为它们都还没有第二代号，标识符为0（假）
        head->next->next = NULL;                                                                 // 第二个人指向NULL（空指针）

        int a_name, a_code, b_name, b_code;                            // 声明四个变量，用于存储每次读入的数据
        for (int i = 1; i < n; i++) {                                  // 由于第一次读过了，只要再读n-1次即可
            scanf("%d,%d->%d,%d", &a_name, &a_code, &b_name, &b_code); // 存入临时变量
            for (struct spy *p = head; p != NULL; p = p->next) {       // 遍历（扫描、搜索）链表，目的就是插入目标的结构体和其所附带的信息
                if (head->name == b_name) {                            // 这是判断head是否指向b，因为按这个思路，只用p判断的话判断不到这种情况，此作为一种特例的补充
                    if (head->code1 != b_code) {                       // 判断有没有第二个代号
                        head->is_code2 = 1;                            // 有第二代号，标识符为真
                        head->code2 = b_code;                          // 写入第二代号
                    }

                    struct spy *to_insert;                  // 创建一个待插入的结构体的指针
                    to_insert = malloc(sizeof(struct spy)); // 分配内存，和之前一个道理
                    to_insert->name = a_name;               // 给结构体写入name信息
                    to_insert->code1 = a_code;              // 给结构体写入代号信息
                    // 下面两句是插入的操作
                    to_insert->next = head; // 新插入对象指向之前的第一项
                    head = to_insert;       // 现在的head指向新插入对象
                    break;                  // 及时退出循环，防止修改到其他数据
                }
                if (p->name == a_name) {      // 这是判断是否要前插（即p是a，即在p->next前插入b）
                    if (p->code1 != a_code) { // 判断并写入第二个代号
                        p->is_code2 = 1;
                        p->code2 = a_code;
                    }
                    if (p->next != NULL && p->next->name == b_name && p->next->code1 != b_code) { // 判断b有没有第二个代号（针对第四个输入样例那样的判断）
                        p->next->is_code2 = 1;                                                    // 标识符为真
                        p->next->code2 = b_code;
                    }

                    if (p->next == NULL || (p->next != NULL && p->next->name != b_name)) { // 字面意思，其中前一个 p->next == NULL 是防止它不读最后一个了
                        struct spy *to_insert;
                        to_insert = malloc(sizeof(struct spy));
                        to_insert->name = b_name;
                        to_insert->code1 = b_code;
                        // 插入的操作
                        to_insert->next = p->next; // 新插入对象的next，赋值为原来p的next
                        p->next = to_insert;       // 现在p的next是新插入对象
                    }
                    break;
                }
                if (p->next != NULL && p->next->name == b_name) {
                    if (p->next->code1 != b_code) { // 判断有没有第二个代号
                        p->next->is_code2 = 1;      // 标识符为真
                        p->next->code2 = b_code;
                    }

                    struct spy *to_insert;
                    to_insert = malloc(sizeof(struct spy));
                    to_insert->name = b_name;
                    to_insert->code1 = b_code;
                    // 插入的操作
                    to_insert->next = p->next; // 新插入对象的next，赋值为原来p的next
                    p->next = to_insert;       // 现在p的next是新插入对象
                    break;
                }
            }
        }
        int is_first_one = 1; // 是不是输出第一项呢？结合下面的判断，如果是输出第一项，就不打最开始的->，后续都不是第一项，就都打出->
        for (struct spy *p = head; p != NULL; p = p->next) {
            if (!is_first_one)
                printf("->");
            is_first_one = 0; // 只有第一次循环才不执行上面那句代码，后续因为有了这句，所以都会执行
            printf("%d,%d", p->name, p->code1);
            if (p->is_code2) {
                printf("#%d", p->code2); // 这里令我非常无语，把一个井号看成两个，导致一直0%
            }
        }
        printf("\n");
    }
}

一点感想

学习一门学科，是一个从“必然”走向“自由”的过程。必然是客观规律，自由是对必然的认识和对客观世界的改造。比如在学C语言的时候，必然就是许多C语言的特性，大的可能有数据结构、链表、指针这样的内容，小的比如说for循环、while循环的技巧，if判断中的短路规则等等，而自由就是我们对这些特性的认识和运用这些特性解决实际问题的过程。

我们仅仅在书本上了解、认识了客观规律，这还不是自由，只有进一步在实践中正确地运用客观规律，达到了改造世界的目的，才是真正的自由。也就是学习C语言的各种特性，是远远不够的，只有在实践中恰当地运用这些特性，来解决各种实际问题改造世界，才能在C语言的领域中自由遨游，达到“万类霜天竞自由”的境界，自如地运用各种特性，解决各种复杂的问题。恩格斯说：“自由不在于幻想中摆脱自然规律而独立，而在于认识这些规律，从而能够有计划地使自然规律为一定的目的服务。”（《反杜林论》）

这种自由并不是不能达到的，并不是只能对着高深的知识望洋兴叹。必然和自由是对立的统一，在一定条件下是可以互相转化的。刚开始做题，这也错，那也错，这就是受了必然的制约，成了必然的“奴隶”。但是在不断学习和实践中，也就是在一定条件下，必然就会向自由转化，即此时我们了解了C语言的一些特性和它的惯用法、常用技巧等，能运用这些知识解决问题了，这就是得到了自由。我们说一定条件下必然和自由的转化是客观的，是向一加一等于二一样的真理，因此，要相信在一定条件下，必然一定会向自由转化，不要有“学不会”这样的思想。没有什么天生的天才，人的知识都是后天取得的，只要付出了努力，把认识和实践相结合，创造了这其中的“一定条件”，必然就一定能转换成自由，我们也一定能取得成绩。

而对C语言或者其他学科，它们是复杂的，也就是说对这些学科的认识的自由不是一次性就能得到的。必须要经过实践、认识、再实践、再认识的多次反复才能得到。这个规律在人类历史上也是适用的。毛主席说：“人类的历史，就是一个不断地从必然王国向自由王国发展的历史。这个历史永远不会完结。”

另外在学习的时候还想到了实践和认识的问题，要做成一件事，不能只有实践，也不能只有认识，而是在“实践，认识，再实践，再认识”的多次循环反复中实现的。我们说的“知行合一”，绝不是简单的“合一”，说知就是行，行就是知，然后用知代替行，这是唯心主义的“知行合一”。正确的“知行合一”，其实是“知行统一”，毛主席说：“实践、认识、再实践、再认识，这种形式，循环反复以至无穷，而实践和认识之每一循环的内容，都比较地进到了高一级的程度。这就是辩证唯物论的全部认识论，这就是辩证唯物论的知行统一观。”（《实践论》） 我们学习任何学科知识，都要有这样的思想，单纯的看书、单纯的做题都是不行的。而从全局来看，看书和做题其实都是“认识”的步骤，真正的实践还是将知识投入生产，用于改造世界。再从更大的格局来看，这种实践属于个人的实践，不是社会的实践，这就是后话了。