第四章 图像的局部特征 笔记

第四章 图像的局部特征

• 摘要：角点检测（Harris角点检测、SIFT检测）、区域表示（梯度方向直方图、SIFT表示）

图像特征分为：全局特征和局部特征。

1. 全局特征（Global Feature）：

   是指能够描述整幅图像的特征，一般是通过图像中的全部（或大部分）像素计算得到。

   常见的全局特征：颜色直方图、形状描述子、GISI

2. 局部特征（Local Feature）:

   是指基于局部图像块计算得到的。

   常见的局部特征：

   ​ 尺度不变特征变换（Scale-Invariant Feature Transform,SIFT）

   ​ 局部二值模式（Local Binary Pattern,LBP）

全局特征和局部特征是相对的，对于人脸图像，提取其颜色直方图，所提取的就是全局特征；

而对于一幅行人的图像提取其中人脸部分的颜色直方图，提取的就是局部特征。

好的特征应具有以下特点：

（1）具有较强的判断力。（即可以通过该特征区分不同的物体）

（2）具有一定的不变性。

（例如对于旋转、平移以及缩放的不变性，即图像经过旋转、平移以及缩放之后，所提取的特征不发生变化或变化较小）

（3）计算简单。

由于全局特征受遮挡和视角变化等因素的影响比较严重，因此局部特征得到了越来越广泛的应用。

局部特征是基于局部图像块提取的特征，其提取包括两个步骤：

• 针对哪块图像来提取特征
• 提取什么样的特征

可以通过角点检测的方法来选择角点所在的区域作为图像块来提取局部特征。

4.1 角点检测

计算局部特征时，选择图像块标准：

• 具有判别力并且能够跟其他图像块区分开来的图像块
• 要具有旋转、平移以及尺度不变性

具有判断力的图像块可以用来进行两幅图像间匹配，以及用来进行物体的表示。

4.1.1Harris角点的检测

Harris角点检测思想：

对于一个局部的小区域或小窗口，

• 如果在某个方向上移动这个小窗口，窗口内的灰度/颜色都会发生较大变化时，则认为该小窗口包含角点；
• 如果窗口在某一方向移动，窗口内的灰度/颜色发生了较大变化，而在另一些方向上没有发生变化，则窗口包含边缘；
• 如果窗口在图像各个方向上移动时，窗口内的灰度/颜色都没有发生变化，则该窗口就对应于平坦区域。

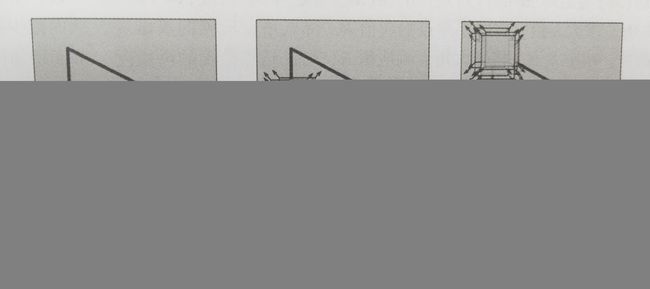
角点如图4-2所示

判断一个像素是否是角点：通过分析矩阵M的特征值

• 当矩阵M的两个特征值都很大，并且两个特征值差别不大时，对应像素就是角点。
• 当两个特征值差别很大时，对应的则是边缘；
• 当两个特征值的绝对值都比较小，对应的是平坦区域

Harris角点检测方法并不需要计算具体的特征值，而是通过计算一个像素的角点相应值R来判断该像素是否是角点。
$$R=det(M)-k(trace(M){)}^2$$
det(M)=λ1*λ2为矩阵M的行列式；trace(M)=λ1+λ2为矩阵M的迹；k为经验常数，取值范围为0.04~0.06.

• 增大k值，将减小角点响应值R，降低角点检测的灵敏度，从而减少检测到的角点的数量；
• 减小k值，将增大角点响应值R，增加角点检测的灵敏度，从而增加检测到的角点的户数量。

计算出R的值可以来判断某个像素点是否是角点。

• 当R值较大时，该像素为角点；
• 当R值为负且绝对值较大时，该像素为边缘；
• 当R值的绝对值较小时，该像素为平坦区域

Harris角点检测的具体算法：

（1）计算图像I(x,y)在x和y两个方向的梯度Ix,Iy

（2）计算图像两个方向梯度的乘积Ix*Iy

（3）使用窗口函数（高斯/常数）对Ix^2 Iy^2和Ix,Iy进行加权求和，生成矩阵M

（4）计算每个像素的Harris响应值R，并将小于某一阈值t的R置为零

（5）在3* 3或者 5*5的邻域内进行非极大值抑制，局部最大值点即为图像中的Harris角点。

Harris角点检测具有以下性质：

（1）Harris角点检测对亮度和对比度的变化不敏感。

即亮度和对比度的变化不会改变Harris响应点的极值点出现的位置，但是选择不同的阈值可能会影响角点检测的数量。

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像的亮度和对比度的变化不敏感。

（2）Harris角点检测具有旋转不变性。

从直观上看，因为角点在旋转后依然是角点。

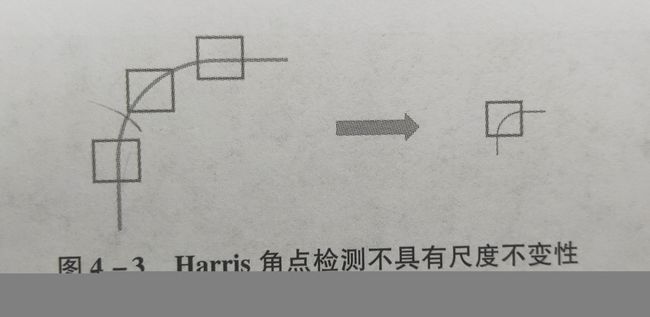
（3）Harris角点检测不具有尺度不变性。

如图4-3

左图：以一定大小的窗口进行角点检测时，检测不到角点，检测到的都是边缘。（左图会被检测为边缘或曲线）

右图：当左图被缩小，检测窗口尺寸不变，当窗口向任意方向移动，窗口内的内容都会发生较大变化。（右图会被检测为角点）

结论：Harris角点检测不具有尺度不变性

4.1.2SIFT的检测

SIFT可以在图像中检测多尺度的特征点。

包括

• 特征点的检测
• 特征点的表示

SIFT步骤：

1. 使用高斯差分（Difference of Gaussians,DOG）来近似计算高斯拉普拉斯（Laplacian of Gaussian,LOG）。
2. 在空间和尺度上寻找局部极值，作为候选特征点。
3. 丢弃对比度较低的候选特征点
4. 为每个特征点设置一个主方向，以得到对于旋转具有不变性的特征表示。

每个步骤细分：

1. SIFT使用高斯差分（Difference of Gaussians,DOG）来近似计算高斯拉普拉斯（Laplacian of Gaussian,LOG）。

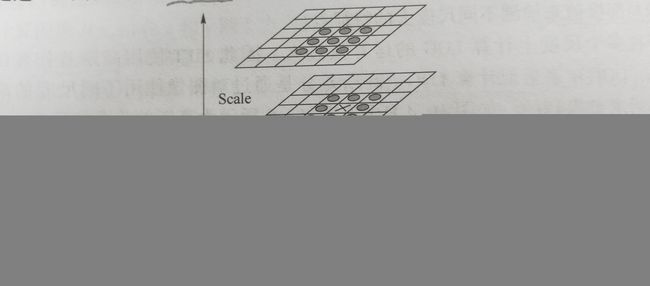
高斯差分是通过对图像使用不同尺度的高斯核进行平滑，然后求差得到的，如图4-4所示。

图4-5所示为高斯差分图像示例。

• 对于原始图像，使用不同尺度的高斯核进行模糊，相邻图像求差得到高斯差分图像。

• 然后再将图像长宽各缩小一半，使用不同尺度高斯核进行模糊，相邻图像求差得到下一级的高斯差分图像。

2. 在空间和尺度上寻找局部极值，作为候选特征点。

• 对于一个像素来说，就是将其与同一尺度上的8个邻近像素以及在上一尺度和下一尺度的18个邻近像素进行比较。
• 若该像素是这26个像素中的极值点，则该像素是一个候选特征点，如图4-6所示。
  -

3. 得到特征点后，丢弃对比度较低的候选特征点

此外，由于DOG对于边缘部分也有较强的响应，因此也需要去除位于边缘上的特征点。

SIFT检测示例如图4-7所示。

• 采用类似Harris角点检测的思想，计算候选特征点对应的2*2的海森矩阵（Hessian Matrix）的特征值

• 若两个特征值的比值大于给定阈值，则说明该候选特征点位于边缘上，应该丢弃该候选点

4. 为每个特征点设置一个主方向，以得到对于旋转具有不变性的特征表示。

计算特征点主方向时，首先应计算其邻域中的梯度方向直方图，直方图中的峰值对应的方向作为特征点的主方向。

• 若其邻域中的梯度方向直方图中有两个或两个以上的峰值，则为每个峰值再分离出一个特征点；
• 若一个特征点邻域内的梯度方向直方图中有两个峰值，则将这个特征点看做是两个特征点，这两个特征点具有相同的位置、尺度以及不同的主方向。

因此，SIFT的特征点包含四个维度的信息，位置(x,y)，尺度(σ)，主方向

4.2区域表示

检测到特征点之后，要在以特征点为中心的一个邻域内建立特征点的表示。

一个好的特征点要具有一定的对于旋转、平移、缩放以及光照变化的不变性。

例如，使用正方形邻域内的像素来表示Harris角点，则Harris角点的检测具有旋转不变性，但是其表示就不具备旋转不变性；

而采用圆形邻域内的像素来表示Harris角点，则该表示就具有对于图像平面内旋转的不变性。

4.2.1 梯度方向直方图

一个好的特征点的表示应该具有以下性质：

• 当中心的位置有少许误差时，该表示的变化不大；
• 当邻域内的大小有少许变化时，该表示的变化不大；
• 当邻域的光照发生变化时，该表示的变化不大；

由于具有较大幅值的梯度比具有较小幅值的梯度更为稳定，因此具有较大幅值的梯度应该在表示中更为重要。

• 直接使用邻域内的像素值来进行区域表示对于光照的变化过于敏感。

• 使用区域内的边缘来进行表示对于光照变化具有一定的不变性。

  • 当光照变亮时，像素间的相对明暗一般不会发生变化。

  • 此时，具有较大幅值的边缘会比具有较小幅值的边缘要更鲁棒。

所以，可以使用邻域内利用梯度幅值加权的梯度方向直方图来表示特征点的邻域。

梯度方向直方图（Histogram of Oriented Gridient,HOG）：

作用：进行区域表示，即目标的外观和形状可以使用梯度方向的分布来进行描述，而无须知道具体的梯度大小和边缘的位置

小问题：直方图不考虑位置信息，不具有判别力

解决：（梯度方向直方图思想）

• 将邻域划分为多个小的窗口
• 在每个小窗口内计算梯度方向直方图
• 并将所有窗口内的梯度方向直方图连接起来作为最终区域的表示

计算步骤：

1. 将梯度方向划分为若干个区间

2. 将图像分为更小的胞元（cells）

3. 计算每个胞元内的一维的梯度方向直方图

   • 将胞元内的每个像素点的梯度方向以梯度幅值作为权重投影到这些区间中，得到一个胞元对应的梯度方向直方图。

   • 一个胞元的梯度方向直方图的维数为所划分的区间的个数，每维的大小为投影到该区间上的梯度幅值之和。

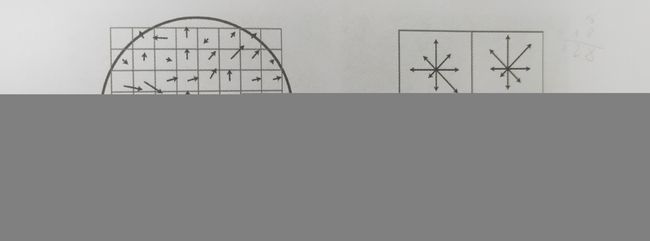
     例如，针对如图4-8所示的梯度方向和梯度幅值，将所有的梯度方向分为9个区间，每个区间的中心角度分别为10°，30°，…，170°，使用梯度幅值的大小作为权重，则计算得到的结如图4-9（a）所示。

   • 小问题：但是这样得到的表达对于噪声或者旋转不具有鲁棒性。

   • 解决：需要将梯度方向通过加权累加到两个相邻的区间中。

     例子：如果某些像素的梯度方向为141°，则这些像素的梯度方向会被累加到中心角度为150°的区间中；如果因为噪声或者旋转影响，梯度方向变为139°，则会被累加到130°的区间中。

     解决：加权累加到两个相邻区间中。

     对于梯度方向为135°的像素，需要将其累加到中心角度为130° 和150°两个区间中，权重分别是0.75和0.25。

     即梯度方向与某个区间的中心角度越接近，则该区间对应的权重越大，通过这种方式得到的梯度方向直方图如图4-9（b）所示。对于旋转和噪声有较好的鲁棒性。

4. 对梯度方向直方图进行归一化（为了对光照等变化具有更好的不变性）

   • 归一化时可以将胞元组成更大的块(blocks)，将块内的所有胞元统一进行归一化。
   • 归一化后的块描述符称为HOG描述子
   • 将检测窗口中的所有块HOG描述子组合起来就形成了最终的特征向量，将其作为对于窗口的特征表示。

总结：

• 将一个窗口划分为若干块，每个块包含多个胞元
• 通过将块中的所有胞元的梯度方向直方图连接起来，得到块对应的梯度方向直方图
• 将窗口中所有块的梯度方向直方图连接起来，就可以得到整个窗口的梯度方向直方图。

窗口内块与块之间是可以有重叠的

论文推荐检测窗口大小：64*128

水平：7个块

竖直：15个块

总块数：7*15=105

每个块有4个胞元，每个胞元包含8*8个像素，块水平移动的步长为一个胞元的宽度，即8个像素。

​ 每个块HOG维数：9*4=36

• 9：所有梯度方向分为9个区间
• 4：每个块有4个胞元

整个窗口的HOG特征向量的维数：105*36=3780

4.2.2 SIFT的表示

在检测到SIFT特征点后，即得到了SIFT特征点的位置、尺度和方向信息后，就需要生成特征点对应的特征向量，SIFT特征点的特征向量的计算包括以下三个步骤：

1. 矫正主方向以得到旋转不变形

   SIFT的表示与HOG非常相似，也是提取特征点的一个邻域，使用邻域内的梯度方向直方图来表示。

   区别：SIFT在计算梯度方向直方图时，是相对特征点的主方向来计算的，从而使计算出的表示具有旋转不变性。

   • 具体以特征点为中心，将坐标轴旋转特征点的主方向对应的角度，即将坐标轴旋转和特征点的主方向重合。

2. 生成128维的特征向量

   SIFT的特征描述符为128维：

   每个梯度方向直方图是8维的，每个特征点表示包括4*4个梯度直方图。8 * 16=128

   如图4-10（为了方便显示，使用2*2个梯度直方图来示意）

   

3. 归一化处理来去除光照的影响

   归一化目的：使SIFT的表示对于光照变化具有不变性，对128维向量进行归一化。

   做法：归一化特征向量，使其模为1

   当图像中像素的梯度幅值整体变大或变小时，所得到的描述符是不变的，然后强制将单位向量中每一维的大小都不能大于0.2。（如果有的维度的值大于0.2，将其设置为0.2，然后重新将向量归一化为模为1的向量）

   目的：避免对梯度幅值很大的像素影响过大，而更多地考虑梯度方向的分布信息。