二叉树的前序遍历 、二叉树的最大深度、平衡二叉树、二叉树遍历（leetcode）

目录

一、二叉树的前序遍历 

方法一：全局变量记录节点个数

方法二：传址调用记录节点个数

二、二叉树的最大深度

三、平衡二叉树

四、二叉树遍历

---

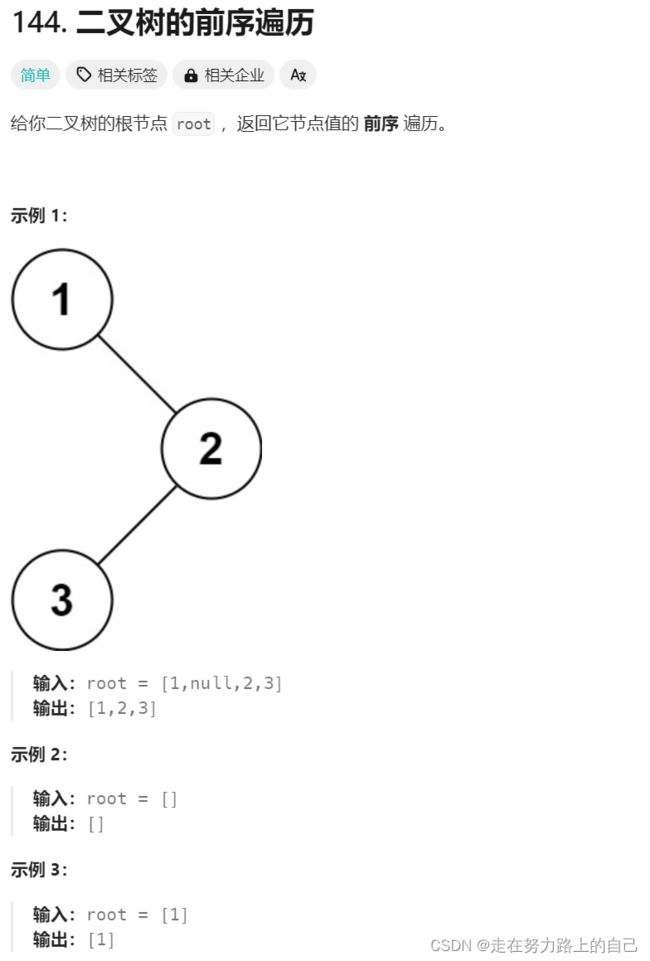
一、二叉树的前序遍历 

 

方法一：全局变量记录节点个数

计算树的节点数:
函数TreeSize用于递归地计算二叉树中的节点数。如果树为空（即根节点为NULL），则返回0。否则，返回左子树的节点数、右子树的节点数和1（表示当前节点）的总和。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;          // 节点的值  
 *  struct TreeNode *left;  // 指向左子节点的指针  
 *  struct TreeNode *right; // 指向右子节点的指针
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
//先求树有几个节点
int TreeSize(struct TreeNode* root)
{
    // 如果树为空（即根节点为NULL），则返回0  
    // 否则，返回左子树节点数 + 右子树节点数 + 1（当前节点）
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

_prevOrder函数:
这是一个辅助函数，用于递归地执行前序遍历。它首先将当前节点的值存储在数组a中，然后递归地遍历左子树和右子树。注意，这里直接使用了全局变量i来更新数组索引。

定义一个全局变量i

// 前序遍历二叉树的辅助函数  
void _prevOrder(struct TreeNode* root, int* a) {  
    // 如果当前节点为空，则直接返回  
    if (root == NULL) {  
        return;  
    }  
    // 将当前节点的值存储到数组中，并使用全局变量i作为索引  
    a[i] = root->val;  
    // 递增全局变量i  
    ++i;  
      
    // 递归遍历左子树  
    _prevOrder(root->left, a);  
    // 递归遍历右子树  
    _prevOrder(root->right, a);  
}

preorderTraversal函数:
这是主函数，用于执行前序遍历并返回结果数组。它首先使用TreeSize函数计算树的节点数，然后动态分配一个足够大的整数数组来存储结果。接下来，它调用_prevOrder函数来执行前序遍历，并填充数组。最后，它设置returnSize为树的节点数，并返回结果数组。

// 执行前序遍历并返回结果数组的主函数  
int* preorderTraversal(struct TreeNode* root, int* returnSize) {  
    //每次调用函数时,都要把i初始化
    //如果没有初始化,则i会一直叠加,无法重复使用
    i = 0;  
    // 调用TreeSize函数计算二叉树的节点数  
    int size = TreeSize(root);  
    // 动态分配结果数组，大小为节点数  
    int* a = (int*)malloc(size * sizeof(int));  
    // 调用辅助函数_prevOrder执行前序遍历，填充数组a  
    _prevOrder(root, a);  
    // 设置返回数组的大小为树的节点数，通过指针参数returnSize返回  
    *returnSize = size;        
    // 返回结果数组a的指针  
    return a;                  
}

方法二：传址调用记录节点个数

前面与方法一相同，不再过多赘述

_prevOrder 函数:
辅助函数，用于递归地执行前序遍历。它接受三个参数：当前节点 root、用于存储遍历结果的数组 a 和一个指向整数的指针 pi（表示当前数组索引）。函数首先将当前节点的值存储在数组 a 的相应位置，然后递增索引 pi。接下来，它递归地遍历左子树和右子树。

// 前序遍历二叉树的辅助函数  
void _prevOrder(struct TreeNode* root, int* a, int* pi) {  
    // 如果当前节点为空，则直接返回  
    if (root == NULL) {  
        return;  
    }  
    // 将当前节点的值存储到数组中，并递增索引pi  
    a[*pi] = root->val;  
    ++(*pi);  
      
    // 递归遍历左子树  
    _prevOrder(root->left, a, pi);  
    // 递归遍历右子树  
    _prevOrder(root->right, a, pi);  
}

preorderTraversal 函数:
这是主函数，用于执行前序遍历并返回结果数组。它首先调用 TreeSize 函数（虽然这里没有给出 TreeSize 的实现，但我们可以假设它的功能是计算树的节点数）来计算树的节点数，然后动态分配一个足够大的整数数组来存储结果。接着，它调用 _prevOrder 函数来执行前序遍历，并填充数组。最后，它设置 returnSize 为树的节点数，并返回结果数组。

int* preorderTraversal(struct TreeNode* root, int* returnSize) {  
    int i = 0; // 初始化索引为0  
    int size = TreeSize(root); // 假设TreeSize函数能正确计算节点数  
    int* a = (int*)malloc(size * sizeof(int)); // 动态分配数组  
    _prevOrder(root, a, &i); // 执行前序遍历，填充数组  
  
    *returnSize = size; // 设置返回数组的大小  
  
    return a; // 返回结果数组  
}

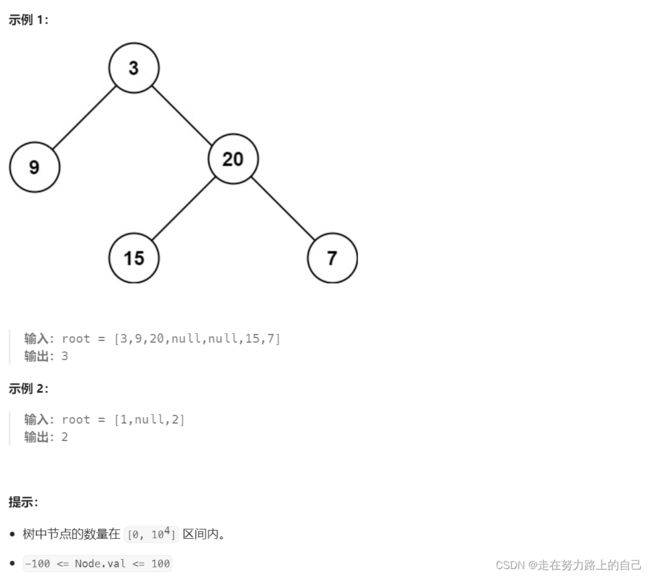
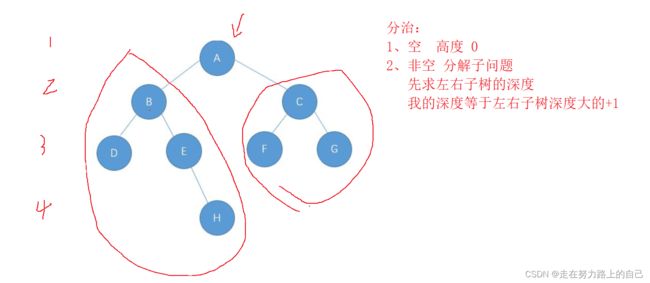
二、二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int maxDepth(struct TreeNode* root) {  
    // 如果根节点为空，说明树是空的，因此深度为0。  
    if (root == NULL)  
        return 0;  
      
    // 递归地计算左子树的最大深度。  
    int leftDepth = maxDepth(root->left);  
      
    // 递归地计算右子树的最大深度。  
    int rightDepth = maxDepth(root->right);  
  
    // 返回左、右子树中深度较大的一个，并加上当前节点的高度1。  
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;  
}

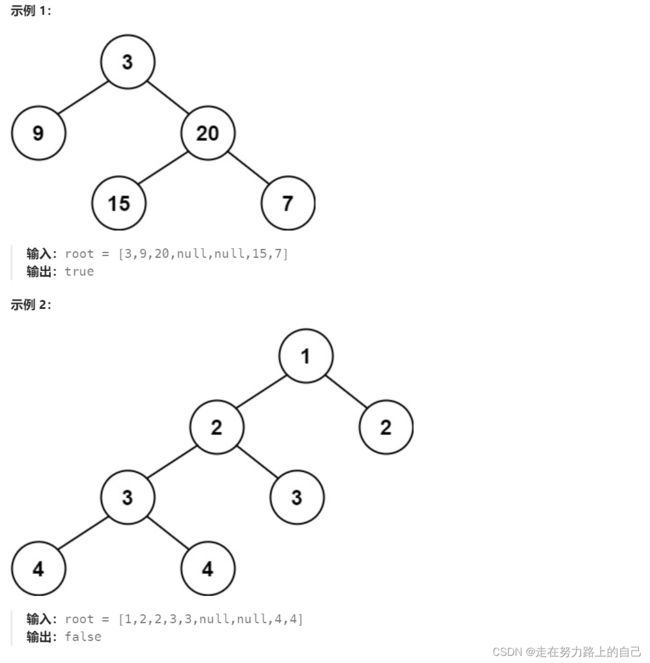
三、平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
 
int maxDepth(struct TreeNode* root) {  
    // 如果根节点为空，说明树是空的，因此深度为0。  
    if (root == NULL)  
        return 0;  
  
    // 递归计算左子树的最大深度。  
    int leftDepth = maxDepth(root->left);  
    // 递归计算右子树的最大深度。  
    int rightDepth = maxDepth(root->right);  
  
    // 返回左、右子树中较大的深度值加1（加上当前节点的高度）。  
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;  
}

bool isBalanced(struct TreeNode* root) {  
    // 如果根节点为空，那么这棵空树被认为是平衡的。  
    if (root == NULL)  
        return true;  
  
    // 计算左子树的最大深度。  
    int leftDepth = maxDepth(root->left);  
    // 计算右子树的最大深度。  
    int rightDepth = maxDepth(root->right);  
  
    // 判断当前节点的左右子树深度差是否小于等于1，并且左右子树本身也都是平衡的。   
    return abs(leftDepth - rightDepth) <= 1  
        && isBalanced(root->left)  // 递归检查左子树是否平衡。  
        && isBalanced(root->right); // 递归检查右子树是否平衡。  
}

四、二叉树遍历

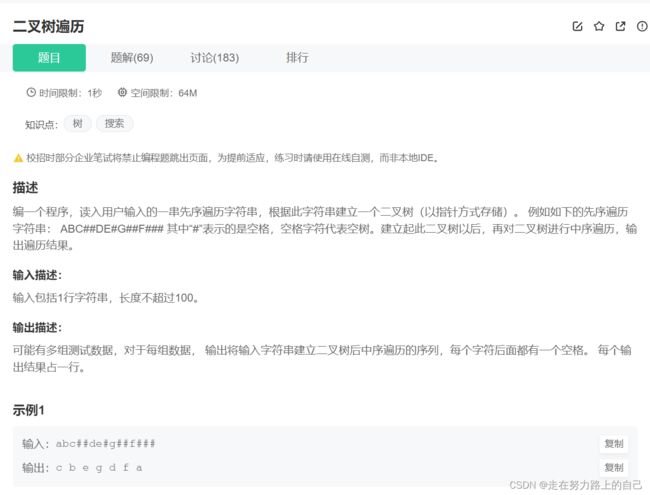
编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。 

#include   
#include  // 需要包含stdlib.h来使用malloc和exit函数  
  
// 定义二叉树节点的结构体  
typedef struct TreeNode  
{  
    struct TreeNode* left;  // 左子树指针  
    struct TreeNode* right; // 右子树指针  
    char val;               // 节点值  
} TNode;  
  
// 创建一个二叉树的函数，a是包含节点值的字符串，pi是指向当前要处理的字符的索引的指针  
TNode* CreatTree(char* a, int* pi)  
{  
    // 如果当前字符是'#'，表示这是一个空节点  
    if (a[*pi] == '#')  
    {  
        ++(*pi); // 增加索引  
        return NULL; // 返回空指针表示这是一个空节点  
    }  
  
    // 为新节点分配内存  
    TNode* root = (TNode*)malloc(sizeof(TNode));  
    if (root == NULL)  
    {  
        printf("malloc fail\n"); // 如果分配失败，输出错误信息  
        exit(-1); // 退出程序  
    }  
  
    // 设置节点的值，并增加索引  
    root->val = a[*pi];  
    ++(*pi);  
  
    // 递归地创建左子树和右子树  
    root->left = CreatTree(a, pi);  
    root->right = CreatTree(a, pi);  
      
    return root; // 返回新创建的节点  
}  
  

// 中序遍历二叉树的函数  
void InOrder(TNode* root) // 注意：函数名应该是InOrder，而不是InOeder（这里有一个拼写错误）  
{  
    if (root == NULL) // 如果节点为空，直接返回  
        return;  
    InOrder(root->left);  // 遍历左子树  
    printf("%c ", root->val); // 输出节点的值  
    InOrder(root->right); // 遍历右子树  
}  
  
int main() {  
    char str[100]; // 存储节点值的字符串  
  
    scanf("%s", str); // 读取输入字符串，注意应该直接传入数组名
    int i = 0; // 索引初始化为0  
    TNode* root = CreatTree(str, &i); // 创建二叉树，并将根节点赋值给root  
    InOrder(root); // 中序遍历二叉树并输出结果  
  
    return 0; 
}

祝大家新年快乐！！！

看到这里了还不给博主扣个：
⛳️ 点赞☀️收藏 ⭐️ 关注！

你们的点赞就是博主更新最大的动力！
有问题可以评论或者私信呢秒回哦。